Лекция по географии. Лекция_03. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
 Скачать 1.14 Mb.
|
Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.Пусть в пространстве имеется декартова система координат Oxyz. С ней связан стандартный базис из единичных взаимно перпендикулярных векторов, расположенных вдоль осей Ox, Oy, Oz. Эти базисные ве 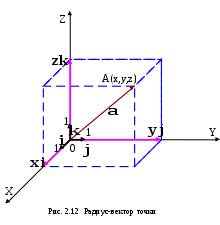 ктора обозначаются через  , , .Выясним связь между введёнными ранее понятиями координат точки в системе Oxyz и вектора в базисе { , , }.Определение. Вектор, начало которого находится в начале координат,а конец в точке A, т.е. вектор  , называется радиус–вектором точки A.Если (x,y,z) – координаты точки A в системеOxyz, то радиус–вектор можно записать в виде =x +y +z . Поэтому координаты точки A(x,y,z) в системе Oxyzи вектора  в базисе { , , } – это одни и те же числа.Теорема. Пусть в декартовой системе координат Oxyz заданы две точки A(xA,yA,zA) и B(xB,yB,zB), тогда в базисе { , , } вектор  имеет координаты ((xВ– xА),(yВ–yА),(zВ–zА)).Доказательство. Запишем вектор  в виде: = – = +(–1) и воспользуемся результатом предыдущей теоремы для базиса {  }, получим: .Пример3. ПустьA(1,–1,1), B(2,3,4), тогда в базисе {  , , } = +4 +3 , т.е. ={1,4,3}.Иногда координаты вектора в базисе { , , } удобно представлять себе в виде проекций.Определение. Проекцией вектора 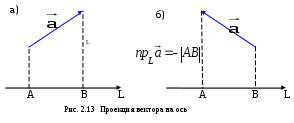 на координатную ось L называется длина проекции вектора  на L, взятая со знаком “+”, если угол между и положительным направлением оси острый, и “–“, если он тупой.  При параллельном переносе вектора, его проекция на ось L не меняется. Проекция обозначается символами  . Несложно проверить, что  = и  = + . Очевидно, что если  имеет координаты  то   ,   ,   .Отсюда получим следующую теорему. Теорема. Пусть вектор имеет координаты  в базисе  , тогда  ,   ,   .Определение. Проекцией вектора 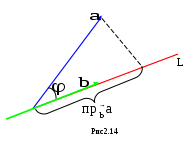 на ненулевой вектор  (обозначение  ) называется его проекция на ось L, проведенная через вектор (см. рис. 2.14). § 2.5. Скалярное произведение векторов и его свойства Имеются три вида произведений векторов: скалярное, векторное и смешанное. Название первого из них произошло от слова скаляр – число. Скалярная величина в математике – это величина, принимающая численные значения. Определение. Скалярным произведением векторов и  называется число, равное произведению модулей этих векторов на косинус угла между ними, т. е. .Скалярное произведение обозначается символами  .Пример 1. Если  , то  . Пример 2. Пусть точка перемещается вдоль вектора 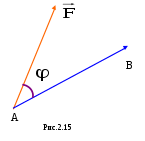 под действием постоянной силы  , сост авляющей угол  с отрезком  (см. рис. 2.15).Тогда из механики известно, что работа этой силы по перемещению точки равна скалярному произведению векторов и  , т.е. .Свойства скалярного произведения 10 Для любых векторов и :  , т.е. это произведение коммутативно. 20 Для любого вектора :.  .30 Скалярные произведение ненулевых векторов и равно  только в том случае, когда эти векторы ортогональны (перпендикулярны).40 Для любых векторов и верно соотношение .50 Для любого вектора с координатами  в базисе  верно ,  ,  .60 Постоянный множитель можно выносить за знак скалярного произведения, т.е. для любых векторов , и числа  верно: .70 Cкалярное произведение обладает свойством дистрибутивности, т.е. для любых векторов  :  .Следствие.  Пример3. Найдем длину большей диагонали 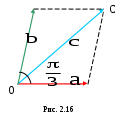 параллелограмма, образованного векторами и , если   ,   (см. рис. 2.16).Поскольку  , то  .Получим формулу для вычисления скалярного произведения в случае, когда векторы заданы своими координатами, а также некоторые следствия из нее. Для определенности будем считать, что все векторы определены в пространстве. Для случая плоскости во всех формулах следует отбросить аппликаты всех векторов (координату  ).Теорема. Пусть в базисе  вектор имеет координаты  , а вектор –  . Тогда .Доказательство. Воспользуемся свойствами 6 и 7 скалярного произведения, получим    .Поскольку базисные векторы  взаимно перпендикулярны, то  , а поскольку эти векторы имеют единичную длину, то  . Подставив эти соотношения в последнее равенство, получим, что .Пример4. Если  , а  , то  .Следствие 1. Если вектор  , в базисе , то .Доказательство.  .Пример5. Если , то .Следствие 2. Косинус угла между векторами  и  равен: .Доказательство. Из соотношения  получим  . Затем для вычисления  воспользуемся теоремой, а для  и  следствием 1. Пример6. Если , , то .Следствие 3. Векторы  и  перпендикулярны только в том случае, когда .Определение. Направляющими косинусами ненулевого вектора называются косинусы углов, образованных этим вектором с осями координат  (см. рис. 2.17). Обычно эти углы обозначаются через  .Следствие 4. Для вектора с координатами  направляющие косинусы записываются в виде: ; ; .Доказательство. Поскольку  , то учитывая, что  из следствия 2 будем иметь: .Остальные формулы доказываются аналогично. 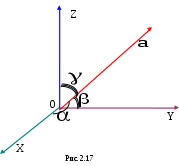 Пример 7. Если  то    Направляющие косинусы вектора обладают следующим свойством. Следствие 5.  Доказательство. Из предыдущего следствия получим:   Определение. Вектор координаты,  которого совпадают с направляющими косинусами вектора  , называется ортом вектора  .Его обозначение  =( ).Орт вектора по модулю равен 1 и сонаправлен вектору .В самом деле из следствия и следует что  т.е. коллинеарен и имеет то же направление. Пример 8. Для вектора  :  . |