Лекция по географии. Лекция_03. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
 Скачать 1.14 Mb.
|
|
§ 2.6. Векторное произведение векторов и его свойства. Это произведение определено только для пространственных векторов  и  , и оно обозначается символами  или  Определение. Векторным произведением векторов и называется вектор   , удовлетворяющий трём условиям:а) Модуль вектора  равен произведению модулей векторов и на синус угла между ними:  sin в)  перпендикулярен векторам и т.е. он перпендикулярен плоскости, проходящей через вектора и .с) Тройка векторов 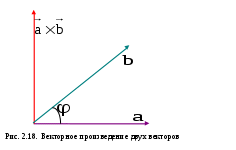 правая (см. рис. 2.18). Пример 1. Найдем  .Поскольку  и  то  Вектор перпендикулярен векторам  , т.е. он направлен вдоль оси  и образует правую тройку с векторами . Этим свойством обладает только вектор  , т.е. .Отметим следующие свойства векторного произведения.  В отличие от скалярного произведения векторное произведение антикоммутативно т.е. для любых векторов  и  верно: . . Ненулевые векторы  коллинеарны только в том случае когда  . . Постоянный множитель можно выносить за знак векторного произведения т.е. для любых векторов  и числа  верно:  . . Векторное произведение обладает свойством дистрибутивности т.е. для любых векторов  верно  .Теорема. Пусть в базисе  векторы имеют координаты  и  соответственно. Тогда в этом базисе  Для запоминания этой формулы используется её запись в виде условного определителя: 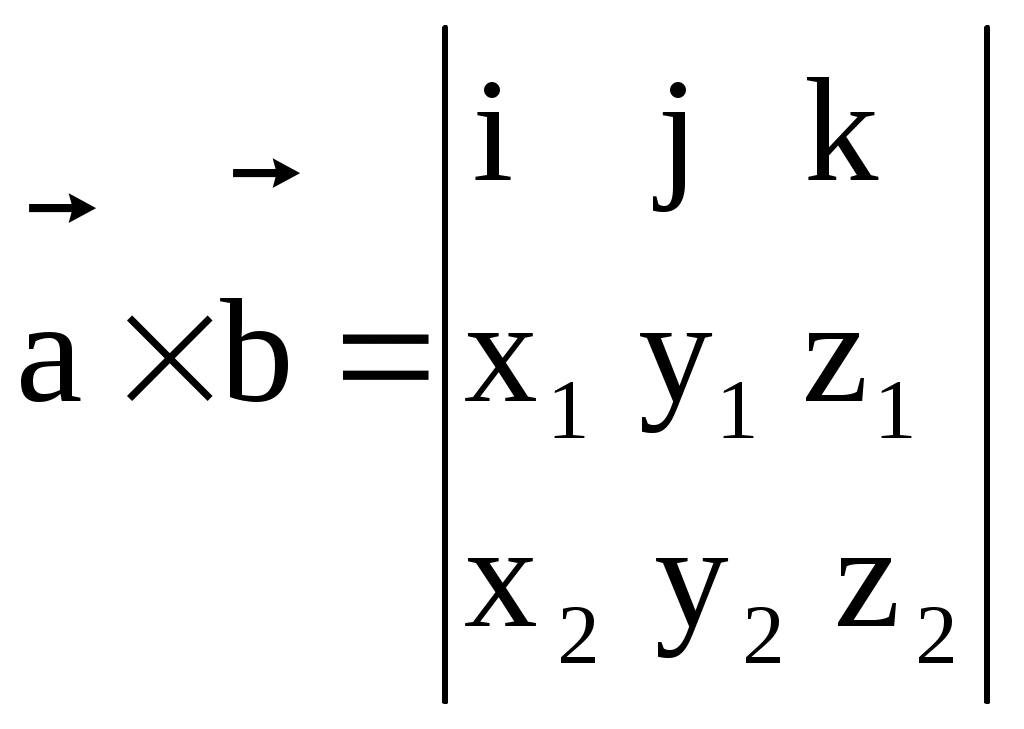 ,который необходимо разложить по первой строке. Пример2. Из того что  следует, что  . Пример3.  .Пример4. Пусть    Найдем  Изза антикоммутативности векторного произведения обычные правила тождественных преобразований для этого произведения не применяются для вычисления модуля вектора используются свойства и определения этого произведения. 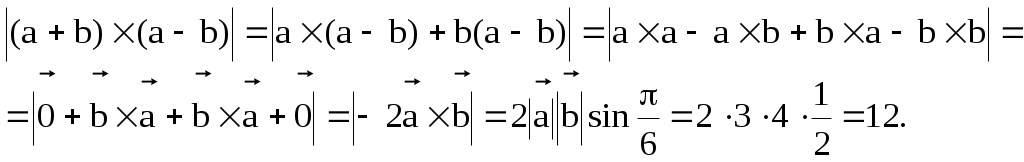 Пример5. Пусть   Найдем 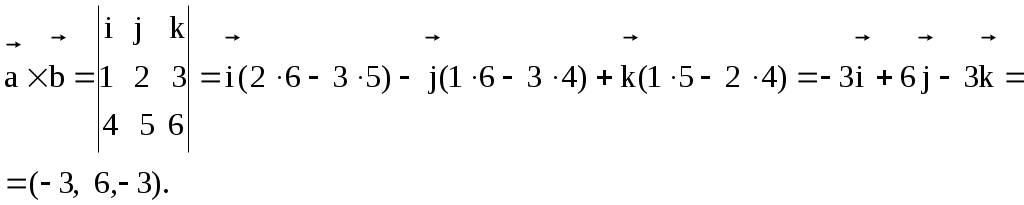 .  Векторное произведение, в частности, применяется для нахождения координат векторов перпендикулярных двум заданным векторам. В последнем примере вектор  перпендикулярен векторам  и образует с ними правую тройку. Другое приложение векторного произведения связано с задачей нахождения площадей. Заметим что модуль векторного произведения  равен площади параллелограмма, построенного на векторах  . Площадь треугольника образованного этими векторами равна  Отсюда получаем следующее. Следствие 1. Площадь параллелограмма построенного на векторах  и  , равна: .Площадь треугольника, построенного на этих векторах, равна:  .Пример6. Найдем площадь треугольника АВС где    Для её нахождения используем векторы 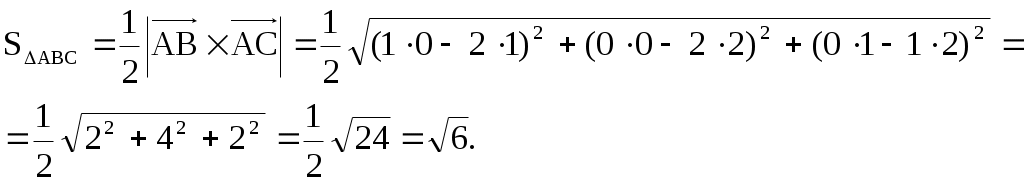 и   Следствие 2. Площадь параллелограмма построенного на векторах  и  , лежащих в плоскости  , равна:  . Площадь треугольника построенного на векторах, равна:  Эти формулы получаются из формул следствия 1 путем подстановки туда  Получим:  .Последнюю формулу можно такие записать в виде: 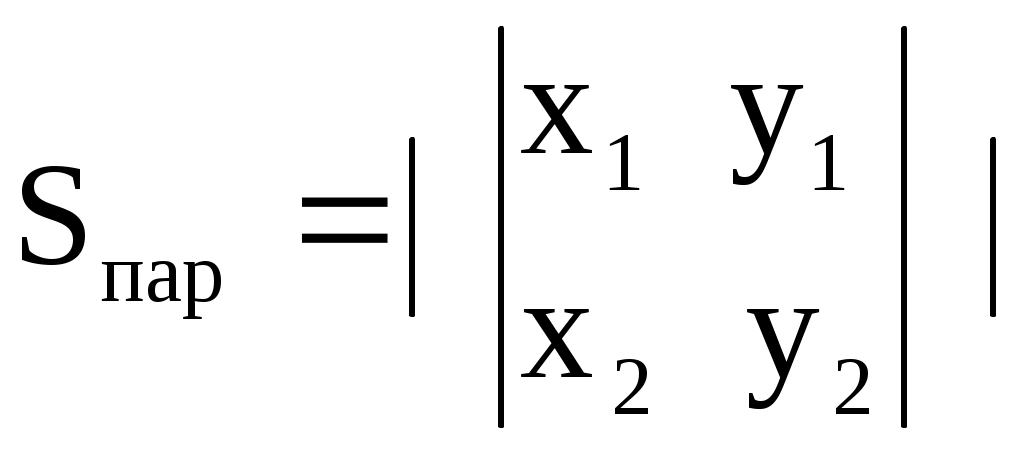 .Другие приложения векторного произведения будут рассмотрены в 11-м модуле, изучаемом в третьем семестре. § 2.7. Cмешанное произведение векторов и его свойства Определение. Смешанным произведением трех векторов  называется число, равное скалярному произведению векторного произведения векторов  с вектором  .Оно обозначается символами  или  : .Свойства смешанного произведения. 10 Смешанное произведение векторов равно  объему параллелепипеда, построенного на этих векторах:  Здесь знак “+” берется в случае если тройка векторов  правая “” если она левая.20 Векторы являются компланарными только в том случае когда их смешанное произведение равно 0:  30 При перестановке местами любых двух векторов смешанного произведения оно меняет свой знак на противоположный; т.е.  4. Постоянный сомножитель можно выносить из любого сомножителя смешанного произведения т.е. для любых векторов  и числа  .5. Смешанное произведение дистрибутивно для любого сомножителя т.е. для любых векторов  верно: .Получим теперь формулу позволяющую находить смешанное про изведение через координаты сомножителей. Теорема. Пусть в базисе 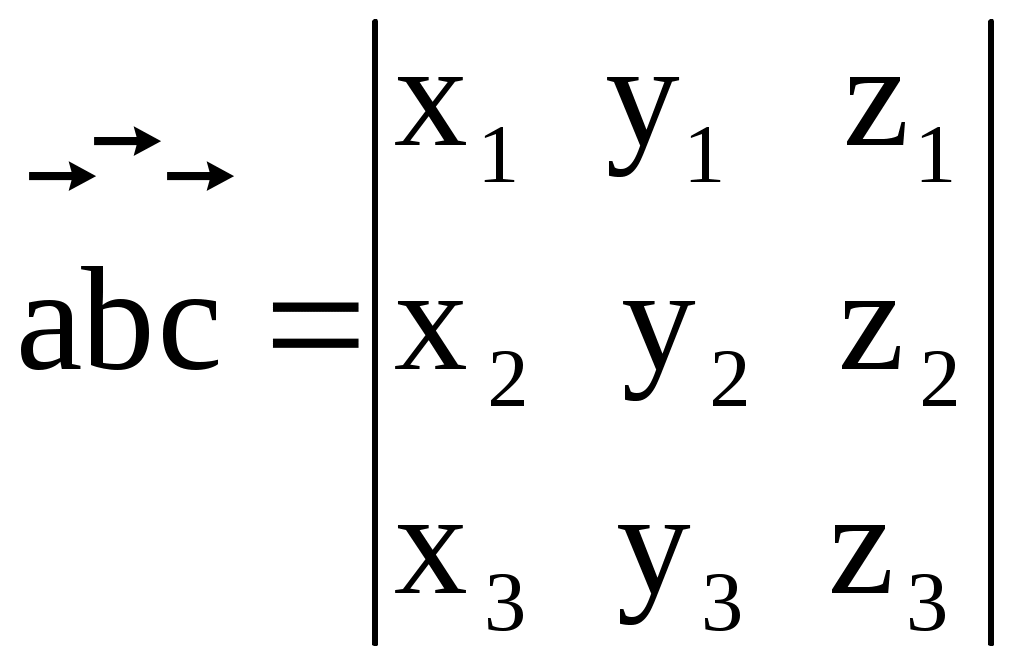 векторы имеют координаты соответственно и  , тогда их смешанное произведение записывается в виде определителя: .Доказательство. Воспользуемся формулами, выражающими векторное и скалярное произведения через координаты сомножителей получим: 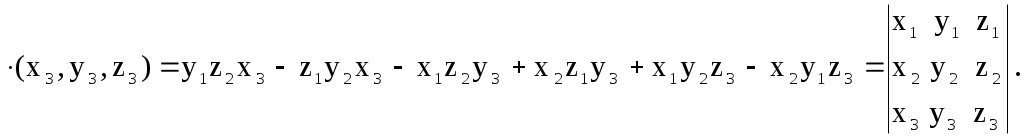  Пример. Проверим образуют ли векторы 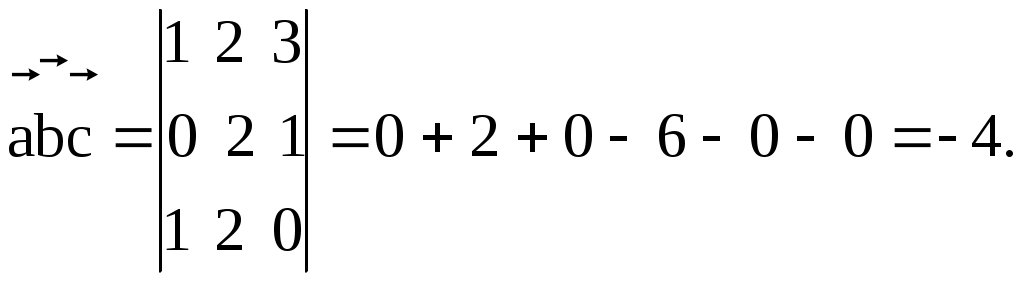   базис. Для этого вычислим их смешанное произведение по правилу Саррюса:  Поскольку  , то эти векторы не компланарны т.е. они образуют базис в пространстве, т.к.  , то этот базис – левый.С помощью полученной формулы для смешанного произведения возможно вычисление объемов некоторых тел. Следствие. Объем параллелепипеда построенного на векторах 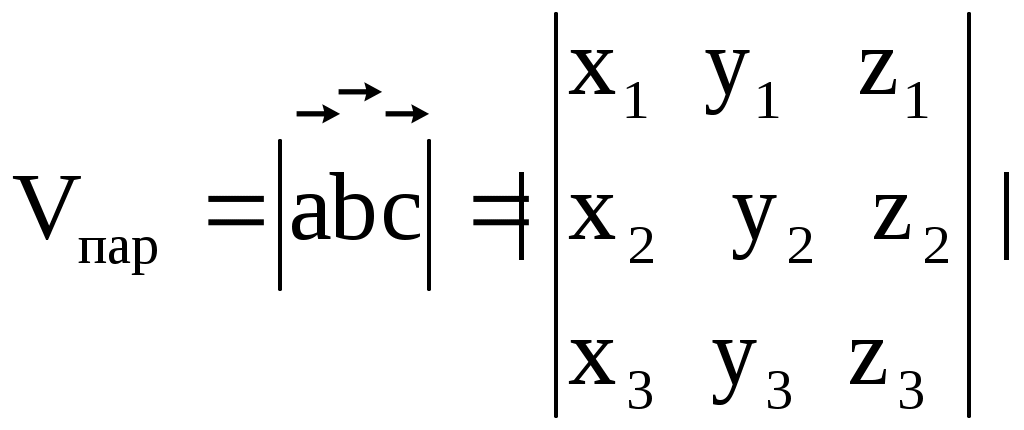   , равен:  .Объем тетраэдра (треугольной пирамиды), образованного этими векторами равен: 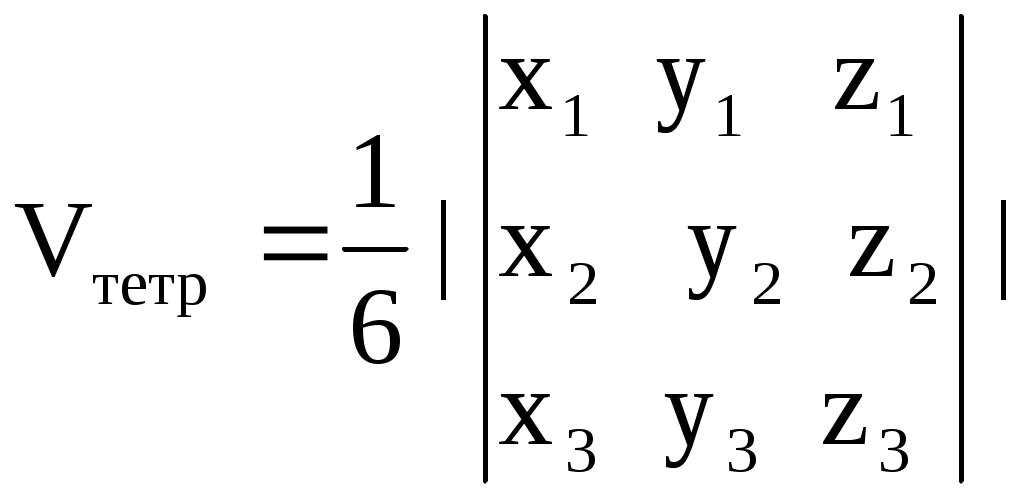 .Пример. Найдем объем тетраэдра с вершинами   и  .Данный тетраэдр образован векторами 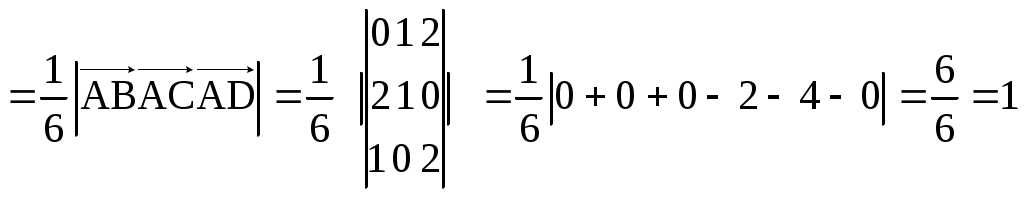 и  , поэтому его объем равен:  .Контрольные вопросы 1.В чем отличие скалярного произведения от векторного произведения векторов? Перечислите основные свойства скалярного и векторного произведений. 2. В чем заключается механический смысл скалярного произведения? 3. Что называется смешанным произведением? 4. В чем заключается геометрический смысл смешанного произведения? Укажите условие коллинеарности двух векторов. Литературы: Основная [1] § 5,6,7 стр. 34-48 [19] 1.3-1.4, 1.10-1.13 стр. 12-20, 66-72, 83-87 Дополнительная [30] Глава 2, § 1,2,3, стр. 41-75 Глава 3 § 1,2,3,4, стр. 76-93 Глава 4 § 1,2, стр. 94-109 Глава 5 § 1,2,3,4,5 стр. 110-142 |