курсовая мка. Демонстрация алгоритма кластеризации сдвига среднего значения
 Скачать 197.69 Kb. Скачать 197.69 Kb.
|
|
Министерство НАУКИ И ВЫСШЕГО образования Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет»  Институт Информатики Институт Информатики Кафедра Кафедра КУРСОВАЯ РАБОТА по дисциплине «Методы кластерного анализа» на тему: «Демонстрация алгоритма кластеризации сдвига среднего значения» Выполнил(а) студент(ка) группы очной формы обучения  (Ф.И.О.) Руководитель: профессор д.ф.-м.н, профессор кафедры  (Ф.И.О.) Дата сдачи: «_____» _________ 2021 г. Дата защиты: «_____» _________ 2021 г. Оценка: _________________ ______________________________ (подпись руководителя) Красноярск 2021 г
Дата выдачи задания «____» ___________ 2021 г.  Подпись научного руководителя Подпись научного руководителяЗадание принял к исполнению «____» ___________ 2021 г. Подпись студента ________________________ СОДЕРЖАНИЕ Преимущества и недостатки Ниже приведены некоторые преимущества алгоритма кластеризации Mean-Shift: 6 Недостатки Ниже приведены некоторые недостатки алгоритма кластеризации Mean-Shift: 7 Введение В алгоритме K-средних на конечный эффект кластеризации влияет начальный центр кластеризации. Предложение алгоритма K-средних ++ обеспечивает основу для выбора лучшего начального центра кластеризации. Однако в алгоритме категории кластеризации число k по-прежнему необходимо определить заранее. Для набора данных, количество категорий которого заранее неизвестно, K-средним и K-средним ++ будет сложно его найти более точно. Для этого были предложены некоторые улучшенные алгоритмы. Концепция сдвига среднего значения была впервые предложена в 1975 году, а затем расширена, в основном предлагая два улучшения: была определена функция ядра и увеличен весовой коэффициент. Определение функции ядра заставляет вклад значения смещения в вектор смещения изменяться в зависимости от расстояния между образцом и точкой смещения. Весовой коэффициент позволяет различным образцам иметь разный вес. Алгоритм сдвига среднего значения успешно применяется во многих областях, таких как сглаживание изображений, сегментация изображений, отслеживание объектов и т.д. Они являются частью искусственного интеллекта или компьютерного зрения, а также он включает традиционные приложения кластеризации. 1. Сглаживание изображения: сжатие пикселей при максимальном качестве изображения; 2. Сегментация изображений: приложение, похожее на сглаживание изображений, но в конечном итоге это разделение изображений, которое можно сгладить для достижения цели фоновой или фиксированной физической сегментации; 3. Слежение за целями: например, динамическое слежение за человеком на камерах видеонаблюдения; 4. Обычная кластеризация, например кластеризация пользователей. Глава 1. Теория алгоритма сдвига среднего значения Алгоритм сдвига среднего значния - это непараметрическая техника анализа пространства признаков для определения местоположения максимума плотности вероятности, основанная на оценке плотности ядра, которую можно использовать для кластеризации, сегментации изображений, отслеживания и т.д. Сдвиг среднего значения является процедурой для определения местоположения максимума плотности вероятности, задаваемой дискретной выборкой по этой функции. Метод является итеративным, и мы начинаем с начальной оценки x. Пусть будет задана ядерная функция K( 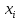 − x). Эта функция определяет вес ближайших точек для переоценки среднего. Обычно используется гауссово ядро от расстояния до текущей оценки − x). Эта функция определяет вес ближайших точек для переоценки среднего. Обычно используется гауссово ядро от расстояния до текущей оценкиK( 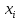 − x)= − x)=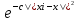 . Взвешенное среднее плотности в окне, определённом функцией K равно . Взвешенное среднее плотности в окне, определённом функцией K равноm(x)= 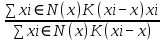 , ,где N(x) является окрестностью точки x, то есть набором точек, для которых K(xi)≠0. Разность m(x)−x в статье Фукунаги и Хостетлера названа сдвигом среднего значения. Алгоритм сдвига среднего значения теперь назначает x←m(x) и повторяет оценку, пока m(x) не сойдётся. Хотя алгоритм сдвига среднего значения широко используется во многих приложениях, строгое доказательство сходимости алгоритма, использующего ядро общего вида в пространствах высокой размерности, отсутствует. Алийари Гассабех показал сходимость алгоритма сдвига среднего значения в одномерном пространстве с дифференцируемой, выпуклой и строго убывающей функцией профиля. Однако случай одной размерности имеет ограниченное применение для реальных задач. Была доказана сходимость алгоритма для случаев высокой размерности с конечным числом (или изолированных) стационарных точек. Однако достаточные условия, чтобы функция ядра имела конечное число (или изолированные) стационарных точек, приведены не были. Принцип алгоритма сдвига среднего значения Ключевой операцией алгоритма является вычисление вектора дрейфа центральной точки посредством изменения плотности данных в интересующей области, чтобы переместить центральную точку для следующей итерации, пока она не достигнет максимальной плотности (центральная точка остается неизменной). Эта операция может быть выполнена для каждой точки данных. В этом процессе подсчитывается количество данных, появляющихся в интересующей области. Этот параметр будет использоваться как основа для классификации в конце. Шаги алгоритма Ниже приведены соответствующие шаги алгоритма кластеризации: 1. Произвольно выберите точку из немаркированных точек данных в качестве центра начальной центральной точки; 2. Найдите все точки данных, которые появляются в области с центром в качестве центра и радиусом в качестве радиуса, и примите во внимание, что эти точки принадлежат одному кластеру C. В то же время запишите количество вхождений точек данных в кластере плюс 1. 3. Взяв центр в качестве центральной точки, вычислите вектор, начинающийся от центра к каждому элементу в наборе M, и сложите эти векторы, чтобы получить сдвиг вектора. 4. Центр = центр + сдвиг. То есть центр перемещается в направлении сдвига, а расстояние перемещения равно || сдвиг ||. 5. Повторяйте шаги 2, 3 и 4 до тех пор, пока сдвиг не станет небольшим (т.е. итерация до схождения), запомните центр в это время. Обратите внимание, что все точки, обнаруженные во время этой итерации, должны быть отнесены к кластеру C. 6. Если расстояние между центром текущего кластера C и центрами других существующих кластеров C2 меньше порогового значения при схождении, то C2 и C объединяются, и количество вхождений точек данных объединяется соответственно. В противном случае возьмите C в качестве нового кластера. 7. Повторите 1, 2, 3, 4, 5, пока все точки не будут отмечены как посещенные. 8. Классификация: в соответствии с каждым классом и частотой доступа каждой точки выберите класс с наивысшей частотой доступа в качестве класса текущего набора точек. Преимущества и недостатки Ниже приведены некоторые преимущества алгоритма кластеризации Mean-Shift: Не нужно делать какие-либо модельные допущения, как в случае K-средних или гауссовой смеси. Он также может моделировать сложные кластеры, которые имеют невыпуклую форму. Требуется только один параметр с именем bandwidth, который автоматически определяет количество кластеров. Там нет вопроса локальных минимумов, как в K-средних. Нет проблем, генерируемых выбросами. Не нужно делать какие-либо модельные допущения, как в случае K-средних или гауссовой смеси. Он также может моделировать сложные кластеры, которые имеют невыпуклую форму. Требуется только один параметр с именем bandwidth, который автоматически определяет количество кластеров. Там нет вопроса локальных минимумов, как в K-средних. Нет проблем, генерируемых выбросами. Недостатки Ниже приведены некоторые недостатки алгоритма кластеризации Mean-Shift: Алгоритм среднего сдвига не работает хорошо в случае большой размерности, где количество кластеров резко меняется. У нас нет прямого контроля над количеством кластеров, но в некоторых приложениях нам нужно определенное количество кластеров. Он не может различить осмысленные и бессмысленные способы. Вывод по главе В первой главе мы ознакомились с принципом действия алгоритма кластеризации сдвига среднего значения, его историей и сферой применения. К реализации алгоритма переходим в следующей главе. Глава 2. Программная реализация алгоритма Выбор языка программирования Для разработки программного продукта в качестве языка программирования был выбран язык Python. Это было сделано по нескольким причинам: во-первых, Python имеет богатый выбор библиотек. Нам понадобятся такие как: numpy – работа с массивами и т.д., matplotlib – вывод результатов в форме графиков, pandas – комфортная работа с матрицами. Во-вторых, этот язык был изучен в ходе учебной деятельности, что способствует качественному выполнению работы. Проектирование и реализация алгоритма Для этого нам понадобятся две довольно популярные библиотеки numpy и matplotlib. После этого, мы можем их импортировать и использовать в программе: import numpy as np import matplotlib.pyplot as plt Первая довольно эффективная для выполнения различных математических операций, включая векторные и матричные. Вторая служит для построения графиков. Алгоритм автоматически устанавливает количество кластеров, вместо того, чтобы полагаться на параметр bandwidth, который определяет размер области для поиска. Этот параметр можно установить вручную, но можно оценить с помощью предоставленной estimate_bandwidth функции, которая вызывается, если полоса пропускания не задана. Алгоритм не отличается высокой масштабируемостью, так как он требует многократного поиска ближайшего соседа во время выполнения алгоритма. Алгоритм гарантированно сходится, однако алгоритм прекратит итерацию, когда изменение центроидов будет небольшим. Маркировка нового образца выполняется путем нахождения ближайшего центроида для данного образца. Реализация в Python Это простой пример, чтобы понять, как работает алгоритм Mean-Shift. В этом примере мы сначала сгенерируем 2D-набор данных, содержащий 4 разных больших объекта, а затем применим алгоритм Mean-Shift, чтобы увидеть результат.    Выход: 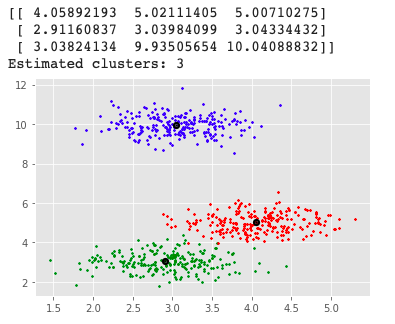 Вывод по главе Во второй главе было представлено описание программной реализации алгоритма сдвига среднего значения. Для этого был выбран язык программирования и программная среда для реализации программного продукта и представлена реализация конечного программного продукта и представлены результаты исследования. Заключение В результате выполнения курсовой работы был реализован алгоритм сдвига среднего значения. Были рассмотрены основные понятия и работа алгоритма. При выполнении курсовой работы были решены следующие задачи: Проведен анализ предметной области и особенностей решаемой задачи. Выбраны средства и язык реализации программной системы. Выполнено тестирование и отладка разработанного программного продукта Результаты исследования показали, что алгоритм среднего сдвига в основном назначает точки данных кластерам итеративно, смещая точки в направлении наивысшей плотности точек данных, то есть центроида кластера. Он имеет ряд своих преимуществ, однако алгоритм имеет и ряд недостатков, но в целом он очень эффективен и удобен. Список использованных источников Yizong Cheng. Mean Shift, Mode Seeking, and Clustering // IEEE Transactions on Pattern Analysis and Machine Intelligence. — IEEE, 1995. — Август (т. 17, вып. 8). Dorin Comaniciu, Peter Meer. Mean Shift: A Robust Approach Toward Feature Space Analysis // IEEE Transactions on Pattern Analysis and Machine Intelligence. — IEEE, 2002. — Май (т. 24, вып. 5). Keinosuke Fukunaga, Larry D. Hostetler. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition // IEEE Transactions on Information Theory. — IEEE, 1975. — Январь (т. 21, вып. 1). ПРИЛОЖЕНИЕ ПРИЛОЖЕНИЕ А %matplotlib inline import numpy as np from sklearn.cluster import MeanShift import matplotlib.pyplot as plt from matplotlib import style style.use("ggplot") centers = [[3,3,3],[4,5,5],[3,10,10]] X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5) plt.scatter(X[:,0],X[:,1]) plt.show() ms = MeanShift() ms.fit(X) labels = ms.labels_ cluster_centers = ms.cluster_centers_ print(cluster_centers) n_clusters_ = len(np.unique(labels)) print("Estimated clusters:", n_clusters_) colors = 10*['r.','g.','b.','c.','k.','y.','m.'] for i in range(len(X)): plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3) plt.scatter(cluster_centers[:,0],cluster_centers[:,1], marker = ".",color = 'k', s = 20, linewidths = 5, zorder = 10) plt.show() |
