Лабораторная работа №1 фомнэ. Дифракция микрочастиц на щели
 Скачать 282.03 Kb. Скачать 282.03 Kb.
|
МИНОБРНАУКИ РОССИИСАНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра МИТ ОТЧЁТпо лабораторной работе № 2 по дисциплине «Физические основы микро- и наноэлектроники» Тема: «Дифракция микрочастиц на щели» Вариант № 16 Студент гр.1191 Пухов А.В. Преподаватель Фантиков В.С. Санкт-Петербург 2022 1 Цель работыЦелью данной работы является ознакомление с понятием единичных фотонов, методикой их получения и ознакомление с опытом, доказывающим корпускулярно-волновую природу фотонов. 2 Основные теоретические положенияКорпускулярно-волновой дуализм является универсальным свойством любых материальных объектов. Это значит, что частица массой m, движущаяся со скоростью υ, характеризуется не только координатами, импульсом р и энергией Е, но и подобно фотону частотой ν и длиной волны λ: Е = h×ν , (1) Любой частице, обладающей импульсом р, соответствует длина волны де Бройля: 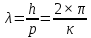 , (2) , (2)где λ - длина волны, м; h - постоянная Планка; Дж·c; р - импульс, кг·м/с; κ - волновой вектор, рад·м-1. Наличие волновых свойств у микрочастиц означает, что можно наблюдать их интерференцию и дифракцию. Поскольку всем микрообъектам присущи и корпускулярные и волновые свойства, то, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. В основу новой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга, легла концепция де Бройля. Это отражается даже в названии волновая функция для величины, описывающей в этой теории состояние системы. Для свободной частицы с точно заданным импульсом, движущейся вдоль оси х, волновая функция имеет вид: 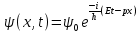 , (3) , (3)Квадрат модуля волновой функции |Ψ(x,t)|² определяет вероятность нахождения частицы в момент времени t в точке с координатой х и может быть найдена путем решения уравнения: 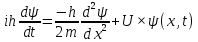 , (4) , (4)где і - мнимая единица; ћ= h / 2×π - редуцированная постоянная Планка (постоянная Дирака); 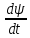 - производная по времени t; - производная по времени t; m — масса частицы; m — масса частицы; 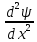 - вторая производная по координате x; - вторая производная по координате x;U – потенциальная энергия частицы, Дж; 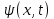 − волновая функция. − волновая функция.Это нерелятивистское волновое уравнение Шредингера для одномерного случая. Релятивистское уравнения для волновой функции является уравнение Клейна-Гордона. Для свободной частицы уравнение Клейна – Гордона записывается в виде: 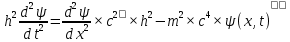 , (5) , (5) где где 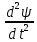 −вторая производная по времени t; −вторая производная по времени t; 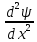 − вторая производная по координате x; − вторая производная по координате x;с — скорость света в вакууме, м/c; m — масса частицы; Частицы, описываемые этой волновой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми. 2.1 Дифракция фотоновДифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных тел, сквозь малые отверстия и т.п.) и связанных с отклонениями от законов геометрической оптики. В частности, дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Явление дифракции заключается в перераспределении светового потока в результате суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно. 2.2 Волновая редукцияВолновая функция непрерывно изменяется во времени. Этот процесс полностью описывается волновым уравнением Шредингера. При взаимодействии квантового объекта с классическим происходит редукция. Этот процесс носит случайный характер, и он не описывается волновым уравнением. В этом случае волновое уравнение позволяет только рассчитать вероятность тех или иных возможных скачкообразных изменений в волновой функции. И если взаимодействие произошло, то волновую функцию следует зачеркнуть и написать новую, с учётом произошедших изменений. Таким образом, редукция волновой функции – это мгновенное и скачкообразное изменение волновой функции, которое не описывается волновым уравнением Шредингера. 3 Экспериментальные результаты3.1 Опыт «Дифракция» 1) Перед началом выполнения лабораторной были изучены методические указания. 2) Был пройден тест на знание материала и готовность к выполнению работы (рисунок 1).  Рисунок 1 - Результаты теста 3) Перешел во вкладку “Дифракция”. 4) Задал настройки - изменил количество частиц, скорость анимации и количество анимированных частиц. 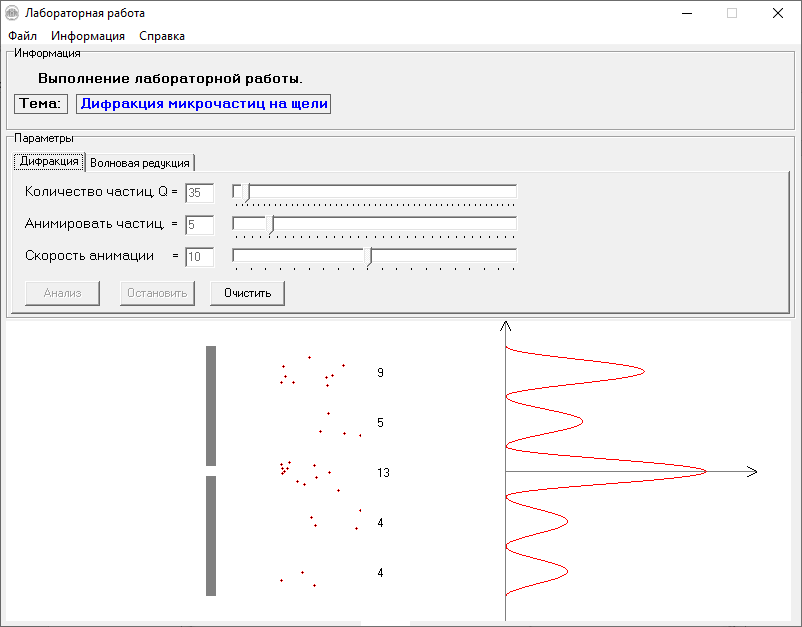 Рисунок 2 - Результаты опыта №1 5) Повторил опыт еще 4 раза, увеличивая количество частиц Q. Результаты каждого из них ниже 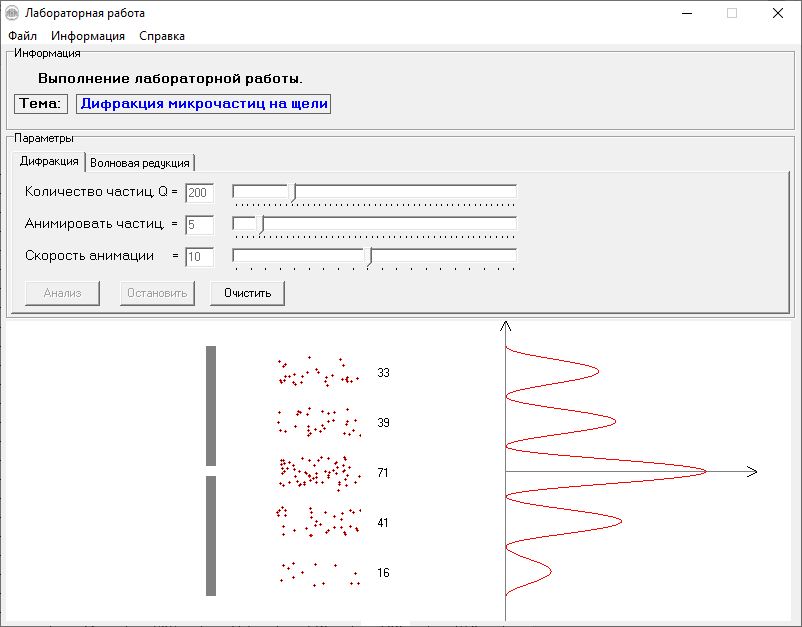 Рисунок 3 - Результаты опыта №2 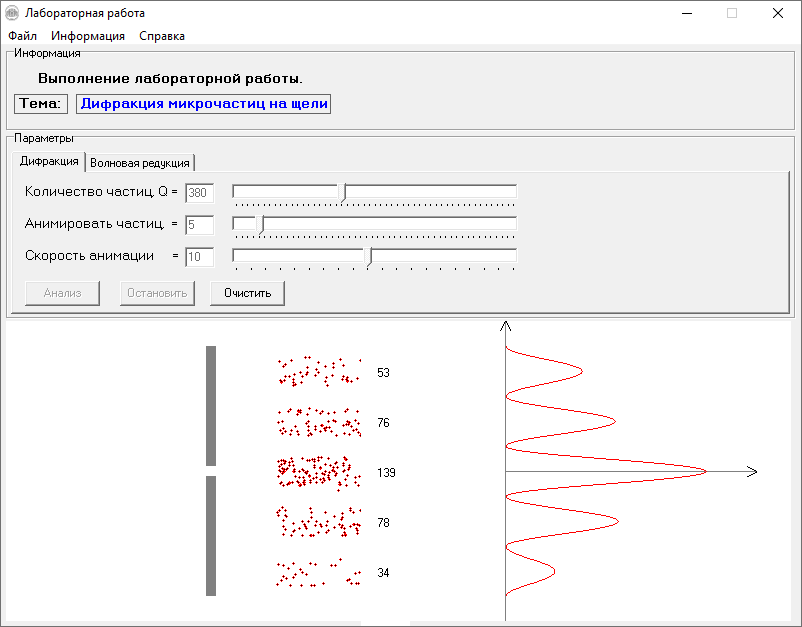 Рисунок 4 – Результаты опыта №3 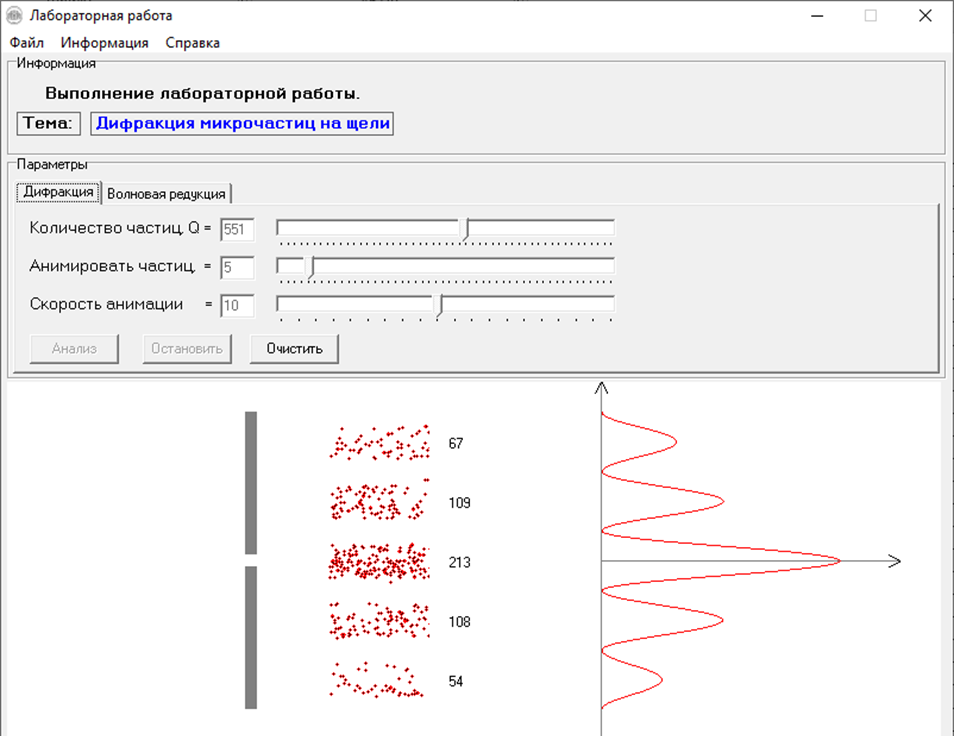 Рисунок 5 - Результаты опыта №4 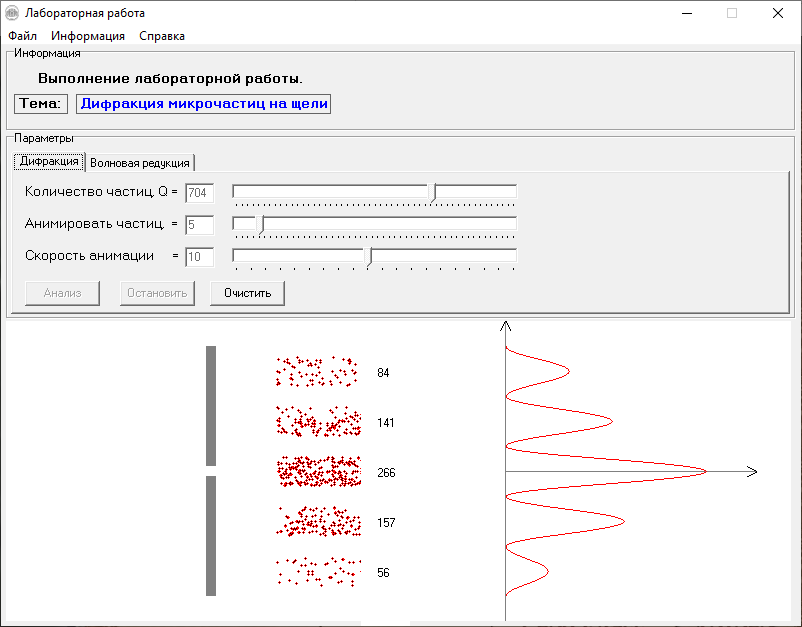 Рисунок 6 - Результаты опыта №5 6) После перезагрузки ПО и теста переходим во вкладку “Волновая редукция”. 3.2 Опыт «Волновая редукция» 1) Выставлены параметры работы приложения, наблюдаем симуляцию волновой редукции. 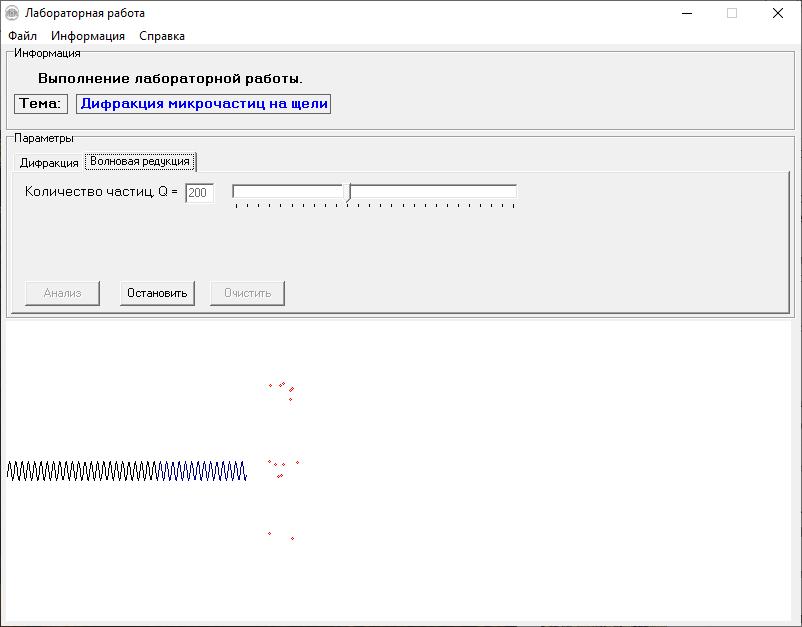 Рисунок 7 - Результаты опыта №1  Рисунок 7 - Результаты опыта №2 4 Выводы: 1) Дифракция фотонов В ходе лабораторной работы наблюдалось распределение одиночных фотонов, проходящих через щель, посредством дифракции. В процессе её выполнения было выяснено, что распределение носит вероятностный характер, т. е. невозможно точно определить координату одиночного фотона во время его полёта, следовательно возможно говорить лишь о вероятности попадания фотона в окрестность определённой точки. Получается, что дифракционная картина на экране за щелью оказывается результатом статического распределения одиночных фотонов на экране, что и доказывает волновую природу света. 2) Волновая редукция Волновая функция непрерывно изменяется во времени. Этот процесс полностью описывается волновым уравнением Шредингера. При взаимодействии квантового объекта с классическим происходит редукция. Этот процесс носит случайный характер, и он не описывается волновым уравнением. В этом случае(ровно каки в случае с дифракцией фотонов) волновое уравнение позволяет только рассчитать вероятность тех или иных возможных скачкообразных изменений в волновой функции. Если имеет место взаимодействие, то функцию необходимо изменить с учетом изменений. Таким образом, редукция волновой функции – это мгновенное и скачкообразное изменение волновой функции, которое не описывается волновым уравнением Шредингера. |
