Работа 1. Лабораторная работа 3 (1). Динамические системы и методы их математического моделирования в пакете Matlab Simulink
 Скачать 363.5 Kb. Скачать 363.5 Kb.
|
|
Лабораторная работа №3 Тема: «Динамические системы и методы их математического моделирования в пакете Matlab Simulink» Цель работы: изучение моделирования систем массового обслуживания в среде GPSS. 1.Задания для лабораторной работы Вариант 1 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов. 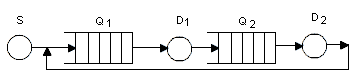 Количество заявок в системе фиксировано и равно 6, они поступают в нее сразу после начала моделирования. Система работает без отказов. Время обработки в D1 величина случайная, распределенная по равномерному закону в интервале от 8 до 12 минут со средним значением 10 минут. Длительность перехода заявки из D1 в Q2 величина случайная, распределенная по равномерному закону в интервале от 35 до 41 минут со средним значением 38 минут. Время обработки в D2 величина случайная, распределенная по экспоненциальному закону со средним значением 14 минут. Длительность перехода заявки из D2 в Q1 величина случайная, распределенная по равномерному закону в интервале от 26 до 30 минут со средним значением 28 минут. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q1 и Q2. Вариант 2 По заданной схеме построить имитационную модель и провести моделирование для 10000 заявок. 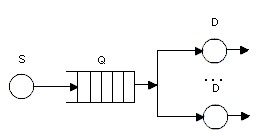 В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя ограниченной емкости равной 10 в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 38 до 42 секунд со средним значением 40 секунд. В отчете отобразить обслуженные и не обслуженные заявки, данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 3 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок. 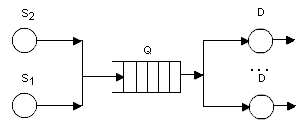 В СМО поступают два класса заявок, заявки первого класса S1 интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд и заявки второго класса S2 интервалы между которыми распределены по равномерному закону в интервале от 20 до 24 секунд со средним значением 22 секунды. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе для заявок первого класса постоянна и равна 20 секундам, для заявок второго класса распределена по экспоненциальному закону со средним значением 20 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 4 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок. 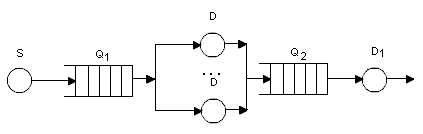 В СМО поступает поток заявок, интервалы между которыми равномерно в интервале от 6 до 10 секунд со средним значением 8 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 35 до 45 секунд со средним значением 40 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 4 до 12 секунд со средним значением 8 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе. Вариант 5 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов. 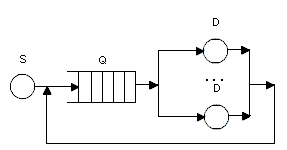 Количество заявок в системе фиксировано и равно 10, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 18 до 22 минут со средним значением 22 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 28 до 32 минут со средним значением 30 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q. Вариант 6 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.  Количество заявок в системе фиксировано и равно 8, они поступают в нее сразу после начала моделирования. Система работает без отказов. Время обработки в D1 величина случайная, распределенная по равномерному закону в интервале от 6 до 14 минут со средним значением 10 минут. Длительность перехода заявки из D1 в Q2 величина случайная, распределенная по равномерному закону в интервале от 32 до 40 минут со средним значением 36 минут. Время обработки в D2 величина случайная, распределенная по экспоненциальному закону со средним значением 10 минут. Длительность перехода заявки из D2 в Q1 величина случайная, распределенная по равномерному закону в интервале от 26 до 30 минут со средним значением 28 минут. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q1 и Q2. Вариант 7 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 14 секунд. Заявки выбираются на обслуживание из накопителя ограниченной емкости равной 14 в порядке поступления. В системе 3 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 36 до 40 секунд со средним значением 38 секунд. В отчете отобразить обслуженные и не обслуженные заявки, данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 8 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступают два класса заявок, заявки первого класса S1 интервалы между которыми распределены по экспоненциальному закону со средним значением 18 секунд и заявки второго класса S2 интервалы между которыми распределены по равномерному закону в интервале от 14 до 20 секунд со средним значением 17 секунды. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе для заявок первого класса постоянна и равна 20 секундам, для заявок второго класса распределена по экспоненциальному закону со средним значением 22 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 9 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступает поток заявок, интервалы между которыми равномерно в интервале от 4 до 10 секунд со средним значением 7 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 6 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 38 до 42 секунд со средним значением 40 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 3 до 9 секунд со средним значением 6 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе. Вариант 10 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.  Количество заявок в системе фиксировано и равно 12, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 20 до 26 минут со средним значением 23 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 30 до 36 минут со средним значением 33 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q. Вариант 11 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.  Количество заявок в системе фиксировано и равно 10, они поступают в нее сразу после начала моделирования. Система работает без отказов. Время обработки в D1 величина случайная, распределенная по экспоненциальному закону со средним значением 10 минут. Длительность перехода заявки из D1 в Q2 величина случайная, распределенная по равномерному закону в интервале от 30 до 40 минут со средним значением 35 минут. Время обработки в D2 величина случайная, распределенная по экспоненциальному закону со средним значением 12 минут. Длительность перехода заявки из D2 в Q1 величина случайная, распределенная по равномерному закону в интервале от 28 до 32 минут со средним значением 30 минут. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q1 и Q2. Вариант 12 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступает поток заявок, интервалы между которыми распределены по равномерному закону в интервале от 6 до 14 секунд со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя ограниченной емкости равной 12 в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 40 до 46 секунд со средним значением 43 секунд. В отчете отобразить обслуженные и не обслуженные заявки, данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 13 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступают два класса заявок, заявки первого класса S1 интервалы между которыми распределены по равномерному закону в интервале от 8 до 12 секунд со средним значением 10 секунды и заявки второго класса S2 интервалы между которыми распределены по экспоненциальному закону со средним значением 18 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе для заявок первого класса постоянна и равна 24 секундам, для заявок второго класса распределена по экспоненциальному закону со средним значением 20 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 14 По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.  В СМО поступает поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 6 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 40 до 44 секунд со средним значением 42 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 3 до 9 секунд со средним значением 6 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе. Вариант 15 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.  Количество заявок в системе фиксировано и равно 10, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по экспоненциальному закону со средним значением 20 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 23 до 29 минут со средним значением 26 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q. Вариант 16 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.  Количество заявок в системе фиксировано и равно 7, они поступают в нее сразу после начала моделирования. Система работает без отказов. Время обработки в D1 величина случайная, распределенная по равномерному закону в интервале от 10 до 16 минут со средним значением 13 минут. Длительность перехода заявки из D1 в Q2 величина случайная, распределенная по равномерному закону в интервале от 32 до 40 минут со средним значением 36 минут. Время обработки в D2 величина случайная, распределенная по экспоненциальному закону со средним значением 15 минут. Длительность перехода заявки из D2 в Q1 величина случайная, распределенная по равномерному закону в интервале от 28 до 30 минут со средним значением 27 минут. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q1 и Q2. Вариант 17 По заданной схеме построить имитационную модель и провести моделирование для 30000 заявок.  В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 13 секунд. Заявки выбираются на обслуживание из накопителя ограниченной емкости равной 8 в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 40 до 46 секунд со средним значением 43 секунд. В отчете отобразить обслуженные и не обслуженные заявки, данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. Вариант 18 По заданной схеме построить имитационную модель и провести моделирование для 15000 заявок.  В СМО поступают два класса заявок, заявки первого класса S1 интервалы между которыми распределены по экспоненциальному закону со средним значением 12 секунд и заявки второго класса S2 интервалы между которыми распределены по равномерному закону в интервале от 18 до 26 секунд со средним значением 22 секунды. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе для заявок первого класса постоянна и равна 24 секундам, для заявок второго класса распределена по экспоненциальному закону со средним значением 20 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. |
