Работа 1. Лабораторная работа 3 (1). Динамические системы и методы их математического моделирования в пакете Matlab Simulink
 Скачать 363.5 Kb. Скачать 363.5 Kb.
|
|
Вариант 19 По заданной схеме построить имитационную модель и провести моделирование для 30000 заявок. 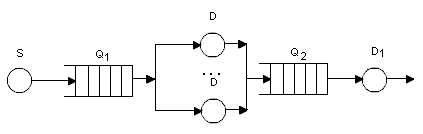 В СМО поступает поток заявок, интервалы между которыми равномерно в интервале от 10 до 14 секунд со средним значением 12 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 38 до 46 секунд со средним значением 42 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 4 до 10 секунд со средним значением 8 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе. Вариант 20 По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов. 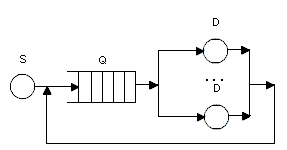 Количество заявок в системе фиксировано и равно 18, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по экспоненциальному закону со средним значением 18 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 20 до 30 минут со средним значением 25 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q. 2. Примеры выполнения лабораторной работы Пример 1. «Одноканальное устройство» По заданной схеме построить имитационную модель и провести моделирование для 10000 заявок. 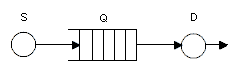 где S – источник заявок, Q – очередь, D – обрабатывающее устройство(канал обслуживания). В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. Длительность обслуживания заявок в устройстве – величина случайная, распределенная по равномерному закону в интервале от 4 до 12 секунд со средним значением 8 секунд. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе. tabl_1 QTABLE ocher,5,10,10; таблица для гистограммы плотности распределения времени ожидания заявок в очереди tabl_2 TABLE M1,10,10,10; таблица для гистограммы плотности распределения времени пребывания заявок в системе GENERATE (EXPONENTIAL(5,0,10)) ; формирование потока заявок QUEUE ocher; отметка момента поступления заявки в очередь SEIZE kan; занятия прибора с именем kan DEPART ocher; отметка момента покидания заявкой очереди ADVANCE 8,4; задержка на время 8±4 единицы времени RELEASE kan; освобождение прибора с именем kan TABULATE tabl_2; регистрирует время покидания заявкой системы TERMINATE 1; удаление заявки из модели START 10000 Рассмотрим подробно представленную модель и прокомментируем каждый оператор GPSS-модели, сопоставив их с реально протекающими в системе процессами. Первыйоператор (команда) QTABLE формирует таблицу для гистограммы плотности распределения времени ожидания заявок в очереди, имя которой указано в операнде A. Имя tabl_1 задаёт имя таблицы (гистограммы), а операнды A, B, C и D задают соответственно: A=ocher – имя очереди, для которой формируется гистограмма; B=5 – верхнюю (правую) границу первого частотного интервала гистограммы; C=10 – величину всех остальных частотных интервалов; D=10 – количество частотных интервалов. Второйоператор TABLE формирует таблицу для гистограммы плотности распределения времени пребывания заявок в системе. Имя tabl_2, как и в предыдущем случае, задает имя таблицы(гистограммы), а операнды A, B, C и D задают соответственно: A=M1 – величину, для которой формируется гистограмма; в нашем примере M1 представляет собой СЧА, определяющее резидентное время, вычисляемое как разность между текущим значением модельного времени, определяемым в момент вхождения транзакта в блок TABULATE, и временем появления транзакта в модели, то есть временем поступления заявки в систему, являющимся одним из параметров транзакта; B=10 – верхнюю границу первого частотного интервала; C=10 – величину всех остальных частотных интервалов; D=10 – количество частотных интервалов. Таким образом, команда TABLE используется совместно с блоком TABULATE, который регистрирует момент прохождения транзактом (заявкой) определенного места в модели. Соответственно блок TABULATE должен находиться в модели в том месте, относительно которого измеряется искомое время. Таким местом при измерении времени пребывания заявки в моделируемой системе является точка выхода заявки из системы, когда транзакт покидает прибор многоканальной системы. В качестве параметра A оператора TABULATE выступает имя соответствующей таблицы (гистограммы). В нашем случае эта таблица и соответствующая ей гистограмма имеет имя tabl_2. Оператор TABLE так же, как и QTABLE, позволяет сформировать гистограмму плотности распределения случайной величины и имеет аналогичную структуру. Основное отличие TABLE от QTABLE состоит в том, что оператор TABLE позволяет формировать гистограмму плотности распределения случайной величины между двумя, в общем случае, произвольными моментами времени, в то время как QTABLE всегда формирует гистограмму плотности распределения времени ожидания в очереди. Оператор GENERATE формирует поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Когда модельное время становится равным моменту формирования очередного транзакта, последний начинает движение в модели к следующему по порядку оператору QUEUE, который заносит транзакт (заявку) в очередь с именем «ocher». Далее транзакт продолжает движение к следующему оператору SEIZE, в соответствии с которым выполняет попытку занять одноканальное устройство (прибор) с именем «kan». При этом проверяется занятость устройства. Если прибор занят обслуживанием ранее поступившего транзакта, то рассматриваемый транзакт приостанавливает свое движение и остается в очереди до тех пор, пока не освободится прибор. Если прибор свободен, то рассматриваемый транзакт продвигается к следующему оператору DEPART. Оператор DEPART отмечает момент покидания транзактом очереди с именем (номером) «ocher» с целью сбора статистики по очередям (определяется время нахождения транзакта в очереди, то есть время ожидания заявки). Двигаясь дальше, транзакт попадает в оператор ADVANCE. Оператор ADVANCE задерживает транзакт на случайную величину, формируемую по равномерному закону распределения из интервала 8±4, моделируя, таким образом, процесс обслуживания заявок в приборе. Дальнейшее движение транзакта в модели возможно только тогда, когда значение модельного времени достигнет момента завершения обслуживания заявки в приборе. При попадании транзакта в операторе RELEASE выполняется совокупность действий по освобождению прибора с именем «kan». Затем транзакт попадает в последний оператор TERMINATE, который выводит транзакт из модели (уничтожает транзакт), при этом из «Счетчика завершений» вычитается значение, указанное в качестве операнда А оператора TERMINATE и равное 1 в нашем примере. Процесс моделирования продолжается до тех пор, пока значение «Счетчика завершений» не станет равным нулю. Начальное значение «Счетчика завершений», указываемое в качестве операнда А, устанавливается с помощью команды START, которая одновременно запускает процесс моделирования. Таким образом, моделирование в данном примере завершится после прохождения через модель 10 тысяч транзактов. По завершению моделирования результаты формируются автоматически в виде стандартного отчета. Но сначала настроим отображаемые данные в отчете. Для этого в главном меню нужно выбрать пункт «Edit/Settings …» и на странице «Reports» («Отчёты») журнала настроек модели с помощью набора флажков задать состав результатов, включаемых в отчёт. Установим флажки напротив: «Queues», «Tables», «Facilities». Теперь запускаем имитацию командой «Create Simulation» в меню «Command». 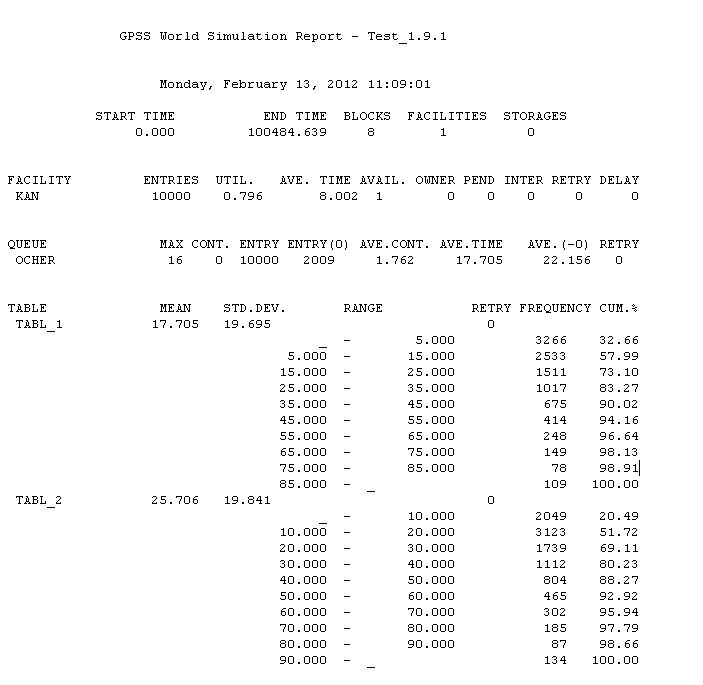 Отчет рассматриваемой модели содержит следующую информацию. 1. Заголовок с именем GPSS-модели: 2. Дату и время проведения имитационного моделирования(эксперимента): 3. Время старта и завершения моделирования, количество блоков(операторов), одноканальных устройств (приборов) и многоканальных устройств (памятей) в GPSS-модели: 4. Результаты моделирования и дополнительная информация по устройствам: Здесь: FACILITY – символическое имя или номер устройства; ENTRIES – количество транзактов, вошедших в данное устройство за время моделирования; UTIL. – коэффициент использования (загрузка) устройства; AVE.TIME – среднее время занятия устройства одним транзактом (средняя длительность обслуживания заявок); AVAIL. – состояние устройства на момент завершения моделирования: 1 -устройство доступно (не занято), 0 - устройство недоступно (занято); OWNER – номер транзакта, находящегося в устройстве на момент завершения моделирования; PEND – количество транзактов, ожидающих выполнения с прерыванием других транзактов; INTER – количество прерванных транзактов на момент завершения моделирования (в списке прерываний); RETRY – количество транзактов, ожидающих выполнения некоторого специфического условия; DELAY – количество транзактов, ожидающих занятия устройства. 5. Результаты моделирования и дополнительная информация по очередям: Здесь: QUEUE – имя или номер очереди; MAX – максимальное количество транзактов в очереди за время моделирования; CONT. – текущее количество транзактов в очереди на момент завершения моделирования; ENTRY – количество транзактов, прошедших через очередь за время моделирования; ENTRY(0) – количество транзактов, прошедших через очередь за время моделирования с нулевым временем ожидания; AVE.CONT. – средняя длина очереди за время моделирования; AVE.TIME – среднее время нахождения транзакта в очереди (среднее время ожидания заявок); AVE.(-0) – среднее время нахождения транзакта в очереди без учета транзактов с нулевым временем ожидания; RETRY – количество транзактов, ожидающих выполнения некоторого специфического условия; 6. Информация по таблицам: 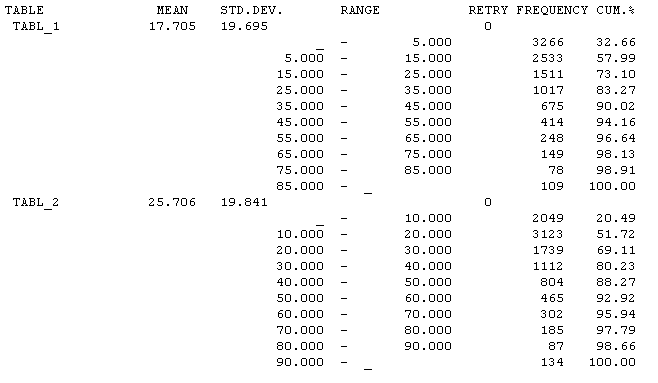 Для каждой из таблиц в отчёте приведены следующие данные: MEAN – среднее значение соответствующей случайной величины; STD.DEV. – стандартное отклонение случайной величины; RANGE – нижние и верхние границы частотного класса (интервала); RETRY – количество транзактов, ожидающих выполнения специфического условия, зависящего от состояния данной таблицы; FREQUENCY – количество случайных значений, попавших в данный интервал; всякий раз увеличивается на единицу, если значение случайной величины больше нижней границы и меньше или равно верхней границе данного интервала; нижняя граница последнего интервала принимается равной бесконечности, то есть все случайные величины, значения которых больше нижней границы последнего частотного интервала, “попадают” в последний интервал; CUM.% - накопленная частота, выраженная в процентах от общего количества случайных значений. Следует отметить наличие определенных проблем, возникающих при задании длин и количества частотных интервалов, задаваемых в качестве операндов команд QTABLE и TABLE. Очевидно, что наглядность и, вытекающая отсюда, информативность гистограмм распределения случайных величин существенно зависит от количества частотных интервалов. Естественно, что для наглядности желательно иметь большое количества частотных интервалов. Однако, чем больше частотных интервалов, тем большую выборку случайных величин необходимо иметь, для того чтобы получить объективную картину, что не всегда возможно и целесообразно. В то же время небольшое количество частотных интервалов (в пределе только 1 интервал) не даёт объективной картины, позволяющей судить о законе распределения анализируемой случайной величины. Таким образом, задание длин и количества частотных интервалов является непростой задачей. Обычно их значения подбираются экспериментальным путем в процессе нескольких реализаций имитационной модели или же на основе предполагаемых значений математического ожидания и среднеквадратического отклонения соответствующей случайной величины. 7. Гистограмма плотности распределения времени ожидания заявок в очереди. 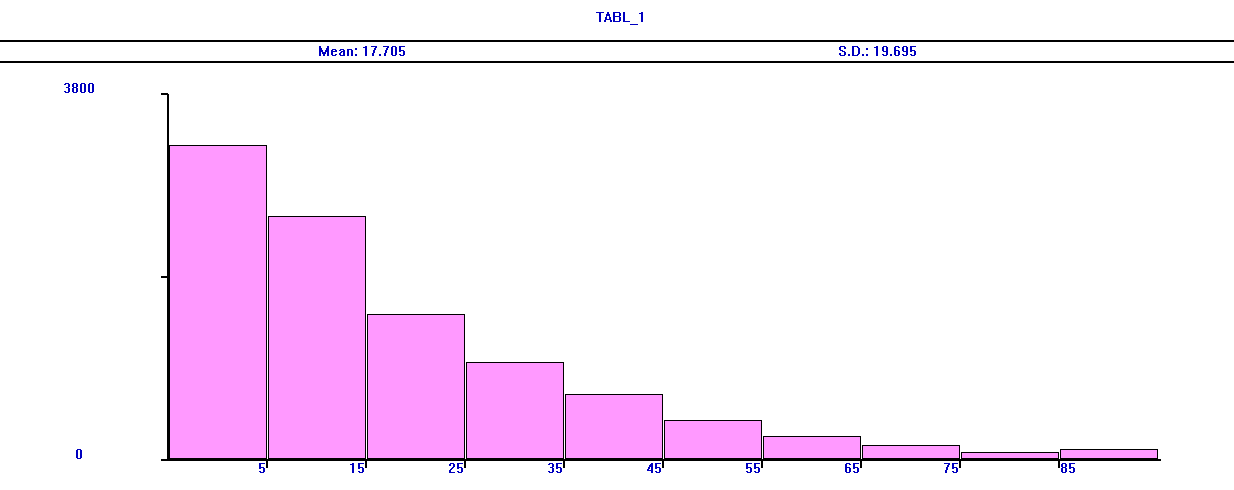 8. Гистограмма плотности распределения времени пребывания заявок в системе. 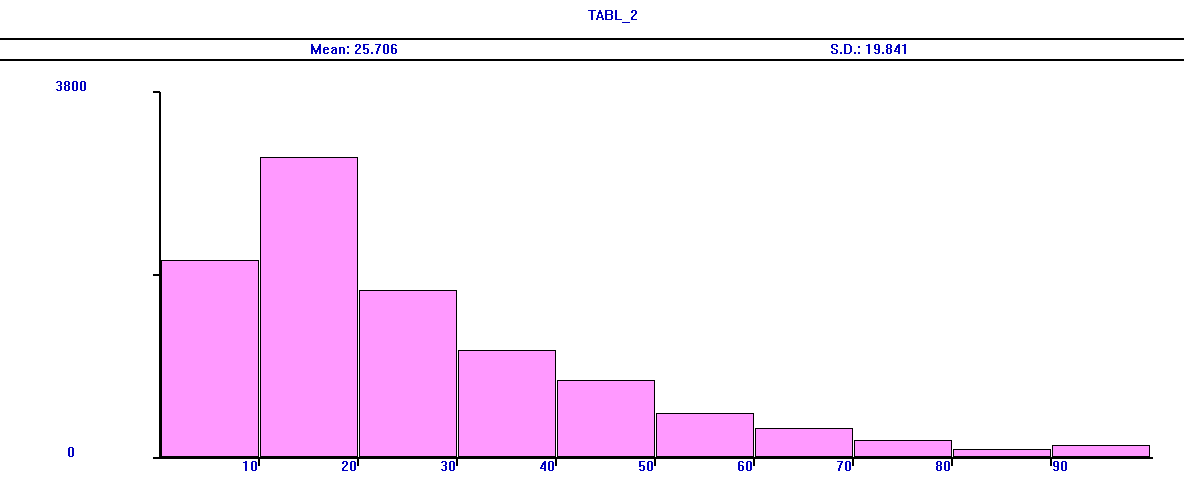 Пример 2. «Многоканальное устройство» По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов. 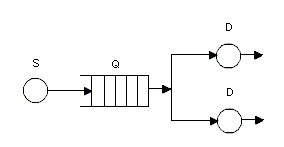 В СМО поступает простейший поток заявок, интервалы между которыми распределены по равномерному закону в интервале от 5 до 9 секунд со средним значением 7 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. Система содержит два идентичных обрабатывающих приборов. Длительность обслуживания заявок в устройстве – величина случайная, распределенная по равномерному закону в интервале от 4 до 12 секунд со средним значением 8 секунд. В отчете отобразить данные по МКУ и очередям. На это раз не будем строить гистограмму, просто уясним способ решения. За единицу времени возьмем 1 минуту. Usel STORAGE 2 GENERATE 7,2 QUEUE Ocher ENTER Usel; попытка занять один из приборов устройства Usel DEPART Ocher ADVANCE 8,4 LEAVE Usel; освобождение одного прибора многоканального устройства Usel TERMINATE GENERATE 480; время моделирования 480 минут TERMINATE 1; уменьшение времени моделирования на 1 минуту. START 1 Рассмотрим изменения, внесенные в предыдущую GPSS-модель. Первое изменениезаключается в появлении в GPSS-модели «Области описания», которая содержит оператор STORAGE, задающий имя (Usel)многоканального устройства (памяти) и количество обслуживающих приборов (ёмкость памяти), равное 2. Второе изменениесостоит в использовании операторов ENTER и LEAVE, моделирующих занятие и освобождение многоканального устройства, вместо операторов SEIZE и RELEASE, использующихся для одноканального устройства. Заметим, что в операторах ENTER и LEAVE, в отличие от SEIZE и RELEASE, могут использоваться два операнда A и B, где второй операнд B определяет количество занимаемых или освобождаемых приборов (каналов), причем при отсутствии операнда B его значение по умолчанию принимается равным 1. Еще одной особенностью данной модели является, то что моделирование заканчивается при превышение времени моделирования. Представим результаты моделирования. Для отображения данных по МКУ, поставить галочку напротив пункта «Storages» в пункте «Edit/Settings …» и странице «Reports». "  Здесь: STORAGE – символическое имя или номер многоканального устройства; CAP. – емкость МКУ; REM. – количество свободных каналов в момент завершения моделирования; MIN. – наименьшее количество занятых каналов в процессе моделирования; MAX. – наибольшее количество занятых каналов в процессе моделирования; ENTRIES – количество входов в МКУ; AVL. - доступность устройства; AVE.C. – среднее количество занятых каналов; UTIL. – коэффициент использования МКУ; RETRY – количество транзактов, ожидающих выполнения некоторого специфического условия; DELAY – количество транзактов, ожидающих занятия устройства. |
