ЛР6 Метрология. Динамический режим средств измерений
 Скачать 242 Kb. Скачать 242 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ИИСТ отчет по лабораторной работе №6 по дисциплине «Метрология» Тема: Динамический режим средств измерений
Санкт-Петербург 2017 Цель работы. Изучение динамического режима средств измерений. Задание. 1. Ознакомиться с лабораторной установкой. Собрать схему исследования динамического звена 2-го порядка. Получить у преподавателя задание на выполнение лабораторной работы. Записать частоту f0 собственных колебаний и коэффициент ß демпфирования (степень успокоения)для заданных вариантов реализации динамического звена. 2. Исследовать динамический режим заданных средств измерений при ступенчатом изменении входного сигнала. 2.1. Определить динамическую погрешность при заданных параметрах звена 2-го порядка и выбранных амплитуде и частоте входных сигналов - прямоугольных импульсов; погрешность определить в 6…10 точках на одном полупериоде входного сигнала. Построить графики входного и выходного сигналов исследуемого средства. Построить графики динамической погрешности. По результатам исследований сделать выводы о влиянии f0 и/или ß на характер изменения выходного сигнала и динамическую погрешность. 2.2. Определить время tу установления выходного сигнала для различных частот f0iсобственных колебаний при заданном коэффициенте демпфирования ß. Построитьграфик зависимости tу = F(f0i) при ß = const. При определении времени установленияпринять погрешность асимптотического приближения переходного процесса, равную 5% от установившегося значения. 2.3. Определить время tу установления выходного сигнала для различных коэффициентов ßiдемпфирования при заданной частоте f0 собственных колебаний. Построить график зависимости tу = F(ßi) при f0 = const. По результатам пунктов 2.2, 2.3 сделать выводы о влиянии f0 и ß на время установления tу. 3. Исследовать динамический режим средств измерений при синусоидальном входном воздействии. Определить погрешности в динамическом режиме при указанных параметрах (f0, ß) звена 2-го порядка и заданной частоте входного сигнала; погрешности определить в 8…10 точках на одном периоде сигнала. Построить графики входного и выходного сигналов, график динамической погрешности. Сделать вывод о характере изменения динамической погрешности и оценить ее максимальное (амплитудное) значение. Основные теоретические положения. Изменение входного сигнала во времени может значительно повлиять на результаты измерений. Важными при этом являются, во-первых, характер изменения сигнала, т. е. его динамические свойства, и, во-вторых, «скорость реакции» средства измерений на входное воздействие, определяемая динамическими характеристиками этого средства. В таких случаях говорят о динамическом режиме средства измерений. При анализе динамического режима средств измерений оказывается весьма удобным рассматривать идеальные и реальные средства измерений, сопоставляя реакцию этих средств на одни и те же входные воздействия. Разность между выходным сигналом y(t) реального средства измерений и выходным сигналом yи(t) (сигнал идеального средства измерений) при одном и том же входном сигнале x(t) определяет динамическую погрешность по выходу реального средства СИр измерений: ∆y(t) = y(t) – yи(t) Структурная схема лабораторной установки (рис. 1). Лабораторная установка состоит из трех основных блоков: – унифицированной вертикальной стойки, включающей источники питания, генератор сигналов прямоугольной, синусоидальной и треугольной формы и измерительные приборы – цифровой частотомер и два цифровых вольтметра; – двухканального электронно-лучевого осциллографа; – специализированного горизонтального модуля, предназначенного для выполнения конкретной лабораторной работы – исследования динамического режима средств измерений.  Рисунок 1 – схема установки Спецификация применяемых средств измерений
Обработка результатов Расчет динамической погрешности при ступенчатом входном воздействии, заданным преподавателем при β = 0,3 и f=800 Гц. Таблица 1- Динамический режим измерений при прямоугольном воздействии
Пример расчета при t=0,2 мс: Uвых= 3.73 В, Uвх= 4,19 В ; ΔU= Uвх-Uвых= 0,46 В   При заданном коэффициенте демпфирования β найдем значения времени t для различных частот f0. Таблица 2- Зависимость времени установления от частоты.
Время t измеряют цифровым чатотометром в режиме измерения временного интервала при старт-стопном запуске.  При заданных частотах найдем значения t для различных коэффициентов демпфирования. Таблица 3- Изменение времени установления от коэффициента демпфирования
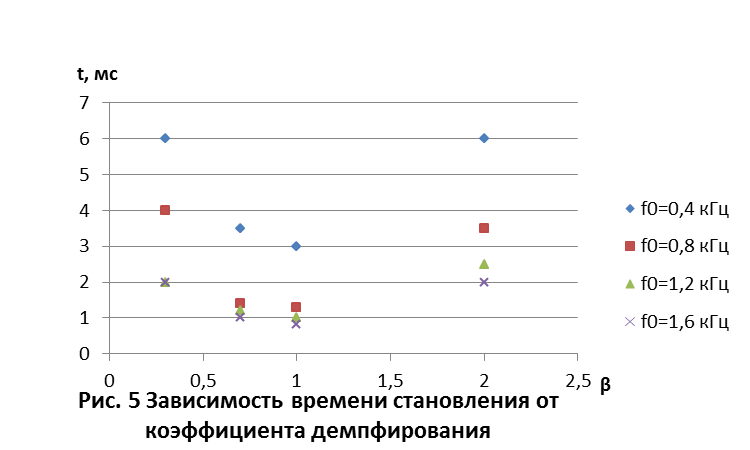 Определим динамическую погрешность при входном синусоидальном воздействии. Динамическая погрешность: ∆U = UВЫХ -UВХ Таблица 4-Динамический режим при синусоидальном воздействии
 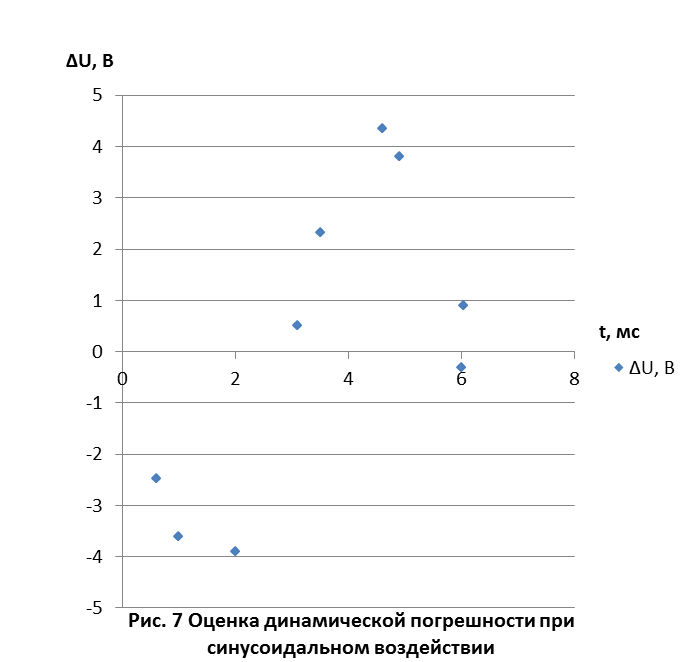 Вывод: Коэффициент демпфирования, применяемый в лабораторной работе, широко распространен в звуковых системах. Также его называют степенью успокоения. Демпфирование - это подавление паразитных колебаний динамической системы громкоговорителя. Благодаря проведенным исследованиям, было выявлено, что при увеличении частоты колебаний фильтра в рамках фиксированного коэффициента демпфирования время установления уменьшается. Также падает и динамическая погрешность. При фиксированной частоте время установления сигнала сначала падает, затем достигает минимума, проходит его, после чего начинает расти. Отсюда делаем вывод, что динамическая погрешность будет минимальна при некотором единственном коэффициенте демпфирования. В нашем случае, это β = 1. При подаче на вход синусоидального воздействия мы получили сигналы, сдвинутые по фазе, причем входной сигнал после прохождения фильтра уменьшился по амплитуде, и имеющие максимальное значение динамической погрешности равной 4,35. При исследовании ступенчатого изменения входного сигнала, мы получили колебания и, соответственно, довольно весомую дополнительную погрешность. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
