динамика. Динамика решение задач (1). Динамика
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Тема динамика 1 пара даем следующую теорию Уравнения Лагранжа II рода можно использовать, когда рассматриваются механические системы с удерживающими, голономными, идеальными связями. Идеальными называются такие связи, когда сумма элементарных работ (возможных мощностей) реакций связей равна нулю. В форме возможных мощностей это условие имеет вид 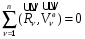 , (3.1) , (3.1)где 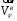 – возможная скорость точки – возможная скорость точки 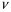 , , 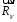 – равнодействующая реакций связей, действующих на точку – равнодействующая реакций связей, действующих на точку 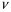 . .Гладкие поверхности, шарнирные соединения, негладкие поверхности, обеспечивающие отсутствие проскальзывания при качении являются идеальными связями. При наличии таких связей движение механической системы с одной степенью свободы описываются одним дифференциальным уравнением 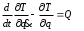 (3.2) (3.2)где 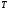 – кинетическая энергия, – кинетическая энергия, 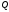 – обобщенная сила, – обобщенная сила, 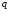 – обобщенная координата, – обобщенная координата, 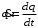 - обобщённая скорость - обобщённая скоростьЗа обобщенную координату могут быть приняты как линейные параметры x, y, так и угловые, например , угол 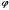 . Им соответствуют обобщенные скорости: линейные vx, vyлибо угловая . Им соответствуют обобщенные скорости: линейные vx, vyлибо угловая 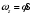 . .Кинетическая энергия твердых тел, входящих в механическую систему, в зависимости от характера движения определяется соотношениями, приведенными на рис. 3.1. Поступательное 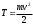 Вращательное вокруг неподвижной оси 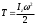 Плоское  Рис 3.1 на рис. 3.1 использованы следующие обозначения: 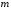 – масса тела, – масса тела,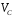 – скорость центра масс, – скорость центра масс, 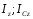 моменты инерции твердых тел относительно осей , проходящих через неподвижную точку моменты инерции твердых тел относительно осей , проходящих через неподвижную точку  или через центр масс или через центр масс 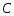 . .На рис. 3.2 приводятся выражения для моментов инерции некоторых однородных тел. 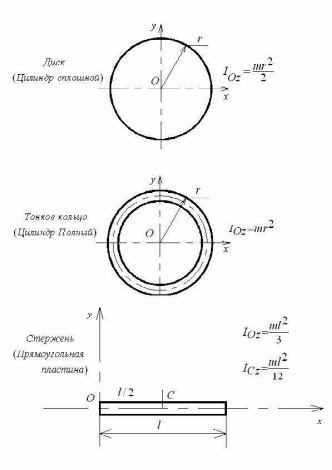 Рис 3.2 Обобщенная сила определяется формулой 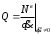 (3.3) (3.3)где  – возможная обобщенная скорость, – возможная обобщенная скорость,  – возможная мощность активных сил. – возможная мощность активных сил.При действии сосредоточенных сил 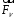 и системы пар сил с моментами и системы пар сил с моментами 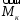 возможная мощность может быть представлена как возможная мощность может быть представлена как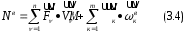 где 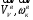 – возможные скорости точек и угловые скорости тел. – возможные скорости точек и угловые скорости тел. Скалярные произведения в соотношениях (3.4) определяются формулами 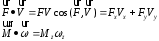 (3.5) (3.5)Из уравнения (3.2) следует, что условие Q = 0 является условием равновесия механической системы в обобщенных координатах. 3.1. Методика решения задач Составление дифференциальных уравнений движения с помощью уравнений Лагранжа II требует последовательного выполнения следующих этапов: Выписать уравнения Лагранжа для заданных обобщенных координат выразить скорости точек и угловые скорости тел через обобщенную скорость и обобщенную координату (эта задача рассматривалась в разделе 2); определить кинетическую энергию как функцию обобщенной скорости и обобщенной координаты, вычислить производные, указанные в левой части уравнения Лагранжа; найти обобщенную силу; подставить найденные выражения в уравнения Лагранжа; Разбираем 1 из примеров: Примеры решения задачПример 1. Составить дифференциальное движение двух ползунов А и В, соединенных невесомым стержнем длиной  . Массы ползунов . Массы ползунов 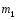 и и 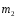 . Обобщенная координата – угол . Обобщенная координата – угол 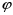 . К стержню приложена пара сил с моментом . К стержню приложена пара сил с моментом 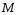 (см . рис 3.3) (см . рис 3.3)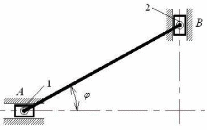 Рис. 3.3 Решение. Составим граф 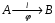 . Запишем соотношение между скоростями точек A и B : . Запишем соотношение между скоростями точек A и B : 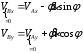 Находим скорости ползунов  Кинетическая энергия 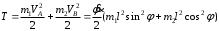 Учитывая , что 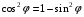 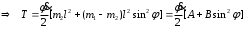 где : 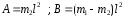 Производные от кинетической энергии 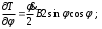 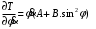 Использовано правило дифференцирования произведения 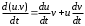 При чём :  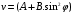 получим : получим : 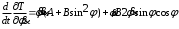 Обобщенная сила 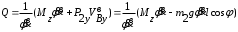 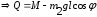 (Мощность силы тяжести 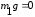 , т.к эта сила и возможная скорость точки , т.к эта сила и возможная скорость точки 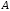 ортогональны ) ортогональны )Дифференциальное уравнение : 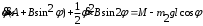 Пример 2. Однородный диск массой 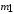 и радиусом и радиусом 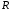 (см. рис. 3.4),к которому приложена пара сил с моментом (см. рис. 3.4),к которому приложена пара сил с моментом 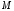 , катится без роскальзывания по неподвижной горизонтальной плоскости. К диску прикреплена материальная точка , катится без роскальзывания по неподвижной горизонтальной плоскости. К диску прикреплена материальная точка 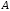 массой массой 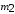 . Принимая за обобщенную координату угол поворота диска . Принимая за обобщенную координату угол поворота диска 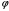 , составить дифференциальное уравнение движения. Момент инерции диска , составить дифференциальное уравнение движения. Момент инерции диска 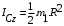 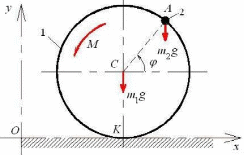 Рис 3.4 Решение. Составим графы 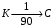 и и 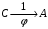 , запишем соотношение между скоростями точек: , запишем соотношение между скоростями точек: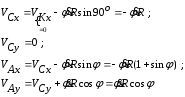 Отсюда находим : 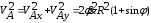 Кинетическая энергия 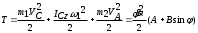 где 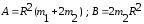 Производные от кинетической энергии 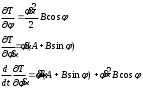 (См . замечание в решении примера 1) Обобщенная сила (учтено , что 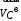 и и 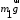 ортогональны) ортогональны) Дифференциальное уравнение 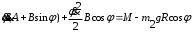 Пример 3. В изображенном на рис. 3.3 кривошипно-кулисном механизме вращательное движение кривошипа 1 преобразуется в возвратно-поступательное кулисы 2. Массы тел – 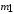 и и 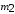 . Кривошип – однородный стержень длиной . Кривошип – однородный стержень длиной 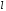 . К кривошипу приложена пара сил с моментом . К кривошипу приложена пара сил с моментом 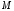 , к кулисе сила , к кулисе сила 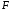 . Составит дифференциальное уравнение движения, приняв за обобщенную координату угол . Составит дифференциальное уравнение движения, приняв за обобщенную координату угол 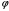 . . Рис. 3.3 Решение. Составим графы 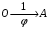 , запишем соотношение между скоростями точек , запишем соотношение между скоростями точек 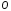 и и 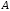 : :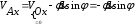 Так как кулиса 2 движется поступательно , то : 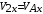 Кинетическая энергия 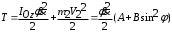 Где 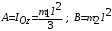 Производные от кинетической энергии 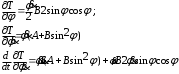 Обобщенная сила 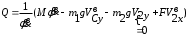 Из графа 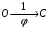 получим получим 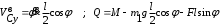 Дифференциальное уравнение 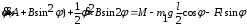 Если осталось время решаем 1 из задач файла D-TST-00.doc 2-3 Пара решаем задачи на линейную координату 4-5 разбираем типовой расчет D-5 кулиса + 2 задачи ИДЗ. D-5 кулиса состоит: Из рукописной части вывод уравнения лагранжа. Решение предлагается в виде решения дифференциального уравнения стандартными методами математических пакетов (оператор D-solve) нахождение реакций предлагается не спрашивать. Или пусть используют кафедеральные программы или программы Ольги Михайловны. |
