Факультативный курс Параметры в геометрии. Дипломная работа Факультативный курс Параметры в геометрии для учащихся восьмых классов общеобразовательной школы

• Название: Дипломная работа Факультативный курс Параметры в геометрии для учащихся восьмых классов общеобразовательной школы
• Дата: 13.12.2021
• Размер: 0.61 Mb.
• Имя файла: Факультативный курс Параметры в геометрии.doc
• Тип: Диплом; #302314
• страница: 3 из 5

Содержание курса

1 занятие (вводная лекция)

Сам термин «параметр» в переводе с греческого означает «отмеривающий». Он обычно применяется в сочетании с другими математическими терминами, например, параметр уравнения, параметр неравенства, параметр функции и т.д. Под задачами с параметрами понимаются задачи, в которых технический и логический ход решения и форма результата зависят от входящих в условие величин, значения которых не заданы конкретно, но должны считаться известными.

Параметр- переменная величина, значение которой позволяет отличить один элемент некоторого множества от других элементов этого множества.

Под геометрическим параметром мы будем понимать любой элемент или элементы геометрической фигуры от величины, расположения или взаимного расположения которых зависит решение задачи, его существование или количество.

Примером одной из первых задач с параметром является знаменитая задача Дидоны. В IX в. до н.э. финикийская царевна Дидона, спасаясь от преследований своего брата, отпра­вилась на запад вдоль берегов Средиземного моря искать себе прибежище, ей приглянулось одно ме­сто на побережье Тунисского залива. Дидона пове­ла переговоры с местным предводителем Ярбом о продаже земли. Запросила она участок совсем не­большой — «столько, сколько можно окружить бычьей шкурой». Дидоне удалось уговорить Ярба, и сделка состоялась. Тогда Дидона изрезала шкуру быка на мелкие тесемки, связала их воедино и ок­ружила большую территорию, на которой основала крепость и город Карфаген. Эта легенда содержит­ся в поэме «Энеида» римского поэта Публия Вергилия Марона, а также в трактате «Об изопериметрических фигурах» древнегреческого ученого Зенодора, жившего между III в. до н.э. и началом н.э.

Задачу по отысканию среди всех замкнутых кри­вых с данным периметром той, которая охватывает максимальную площадь, называют задачей Дидо­ны.

Что же в этой задаче является параметром? Сфор­мулируем задачу Дидоны в таком виде: «у какой фигуры Р, при заданном периметре, площадь бу­дет наибольшей?». В данном случае параметром выступают не числовые данные, а фигура; при раз­личных значениях этого параметра, то есть при различных фигурах задача будет иметь различные решения.

Математика оперирует строго определенными понятиями, а в окружающем нас мире на каждом шагу встречаются сплошные неопределенности, условности. «Если будет дождь, то праздник «День знаний» проходит по программе А, а если дождя не будет, то — по программе Б». Можно ли рассматри­вать условие «будет - не будет идти дождь» как параметр? Или математике нужны только число­вые параметры? Для алгебры — это естественно. Но геометрия включает в себя не только числовые со­отношения между фигурами или элементами фигу­ры, но и геометрические. Следовательно, для гео­метрии параметрами могут быть и классические «алгебраические» параметры, и сугубо специфиче­ские «геометрические» параметры.

В нашем курсе мы будем рассматривать задачи с геометрическими параметрами, а с некоторыми из них вы уже встречались в прошлом году:

1. Точки А, В и С лежат на одной прямой. Известно что АВ = 12см ВС = 13.5см. Какой может быть длина отрезка АС?

Из трех точек прямой одна и только одна лежит между двумя другими. Поскольку речь идет о трех точках, то каждая из них может лежать между двумя другими, и потому мы имеем три раз­личных случая.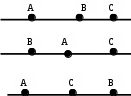




AC=AB+BC=12+13,5=22,5(см)
AC=BC-AB=13,5-12=1,5(см)

AC=AB-BC=12-13,5=-1,5(см)

Отрицательное число не является

решением, так как длина-

положительное число.

Ответ: 22,5см или 1,5см.

2. Известно, что 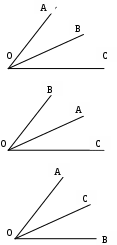АОВ = 35^о, ВОС = 50^о. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира.

AOC= AOB+ BOC=35^о+50^о=85^o
AOC= BOC- AOB=50^о+35^о=15^o


AOC= AOB- BOC=35^о-50^о=-15^o

Отрицательное число не является

решением, так как градусная мера угла - положительное число.
Ответ: 15^o или 85^o.

Домашнее задание

1) Точки А, В и С лежат на одной прямой. Известно что АВ = 10см ВС = 25см. Какой может быть длина отрезка АС? (ответ: 35см или 15см).

2)Известно, что АОВ = 45^о, ВОС = 25^о. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира. (Ответ 70⁰ или 20^о).
3) На прямой расположены точки A,B,C и D. Найдите длину отрезка с концами в серединах AB и CD, если AC = 5, BD = 7.

A D=AC+CB+BD=12+CB

AM=MB B CN=ND

AD=AM+MN+ND=2NM+BC

12+CB=2NM+BC

MN=6

2 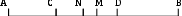) AD=AC+CD=5+CD

AM=MB B CN=ND

AD=AM+ND-NM=MB+CN-NM=MD+7+CN-NM=

=7+CD-2NM

5+CD=7+CD-2NM

MN=1

Ответ: 6 или 1.

2 занятие.(задачи в теме треугольники)

(обобщение задач домашнего задания)
1. На прямой, содержащей отрезок АВ, взята точка С так, что АС=с, АВ=а. Найдите длину отрезка ВС.
Решение.

1) Пусть точка А лежит между точками С и В. Тогда по аксиоме измерения отрезков ВС = АВ + АС, откуда ВС = а + с.

2) Пусть точка В лежит между точками А и С. Тогда АС = АВ + ВС и ВС = с - а.

3) Если же точка С лежит между точками А и В, то АВ = АС + ВС и ВС= а - с.

Очевидно, что случаи 2) и 3) несовместимы, по­скольку значения длины отрезка ВС будут проти­воположны, а длина отрезка - число положитель­ное. Таким образом, один из этих случаев не дает ответа.

Ответ: ВС = а + с или ВС = \а – с\.

2. Луч с выходит из вершины 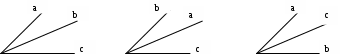(аЬ). Найти (ас), если (аb) = а, (Ьс) = .

р ешение:

(ас)=а- (ас)=а+ (ас)= -а

ответ: /а- / или а+


основная часть

1. Найдите углы равнобедренного треугольника, если один из его углов равен 80^о.




решение:

1) пусть В=80⁰, тогда С=80⁰,

так как треугольник АВС - равнобедренный.

Так как сумма углов треугольника 180⁰, то

А+ В+ С=180⁰

А+160⁰=180⁰

А=20⁰

2) пусть А=80⁰, тогда

А+ В+ С=180⁰

В+ С=100⁰

так как В= С, поскольку АВС – равнобедренный,

то В= С=50⁰

ответ: 20⁰ , 80⁰, и 80⁰ или 50⁰, 50⁰, и 80⁰.

3. 
   Найдите стороны равнобедренного треугольника, если одна из его сторон равна 10, а периметр 26.
   

1 ) пусть АВ=10, тогда АС=10,

так как треугольник АВС - равнобедренный.

Тогда

АВ+АС+ВС=26

ВС=26-10-10=6.
2)пусть ВС=10,

тогда

АВ+АС+ВС=26

АВ+АС=16

так как АВ=АС, поскольку АВС – равнобедренный,

то АВ=АС=8.

Ответ: 10, 10 и 6 или 8, 8, и 10.


3.Через вершины А и С треугольника АВС проведены прямые, перпендикулярные биссектрисе угла АВС, пересекающие прямые СВ и ВА в точках К и М. Найдите АВ, если ВМ = 8, КС = 1.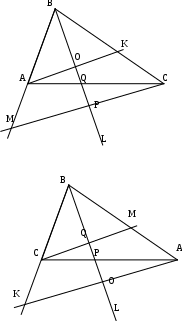



Дано:

АВС, ABL= LBC,AK BL,CM BL,BM=8,KC=1.

Найти АВ.

Решение:

Рассмотрим треугольник АВК:

Равнобедренный, так как ВО - высота

И биссектриса одновременно, следовательно,

АВ=ВК.

Рассмотрим треугольник ВМС:

Равнобедренный, так как ВQ - высота

И биссектриса одновременно, следовательно,

ВМ=ВС.

1. 
   допустим, что АВ

BK=BC=KC=8-1=7

AB=BK=7

2) допустим, что АВ>BC, тогда

BK=BC=KC=8+1=9

AB=BK=9

Ответ: 7 или 9.

4. Биссектриса угла при ос­новании равнобедренного треугольника пересекает боковую сторону под ост­рым углом а. Найдите углы треугольника. При каких значениях парамет­ра а задача имеет два ре­шения?

Решение. Обозначим угол ВАС че­рез 2х.

В зависимости от того, который из углов –

В 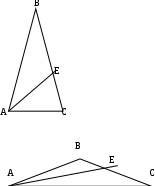ЕС или АЕС - принять равным а,

получатся различные решения.

1) Если АЕС = а, то х + 2х + а = 180°, откуда

х=60°- и В= 120°— . Но поскольку В<90°,

то а>45°. При этом С= -60°.


2) Если АЕС = а, то этот угол как внешний для треугольника АЕС равен сумме двух внутренних

углов, не смежных с ним. То есть а = Зх, а х = .

Тогда В= , С=180°- . Но поскольку

В< 90°, то а < 135°, что уже оговорено в усло­вии задачи (угол а - острый).

Ответ: при а > 45° задача имеет два ре­шения:

А= В=120°- , С= -60°,

или А= В= , С=180°- .
Домашняя работа:

1. 
   Найдите углы равнобедренного треугольника, если один из его внешних углов равен 100^о.
   

р ешение:

1. 
   пусть внешний угол при вершине А=100⁰,
   

тогда С+ В=100⁰,

по теореме о внешнем угле треугольника.

так как треугольник АВС – равнобедренный,

то В= С=50⁰

В=180⁰-100⁰=80⁰

2) пусть внешний угол при вершине В=100⁰, тогда

В=80⁰, следовательно, С=80⁰,

так как треугольник АВС - равнобедренный.

Так как сумма углов треугольника 180⁰, то

А+ В+ С=180⁰

А+160⁰=180⁰

А=20⁰

ответ: 20⁰ , 80⁰, и 80⁰ или 50⁰, 50⁰, и 80⁰.

2. 
   Найдите углы равнобедренного треугольника, если один из них равен а.
   

если угол В равен а, то А= С= ,

Если же А= С=а, то В=180⁰-2а.

ответ: , и а или 180⁰-2а, 180⁰-2а и а.
3. Периметр равнобедренного треугольника ра­вен Р, одна из его сторон равна а. Найдите вторую сторону треугольника.




решение:

1) пусть АВ=а, тогда АС=а,

так как треугольник АВС - равнобедренный.

Тогда АВ+АС+ВС=р, ВС=р-а-а=р-2а.

2)пусть ВС=а, тогда АВ+АС+ВС=р, АВ+АС=р-а

так как АВ=АС, поскольку АВС – равнобедренный,

то АВ-АС= .

Ответ: р-2а, р-2а и а или , , и а.

3 занятие. (задачи в теме окружность)
1. Даны две окружности с общим центром и радиусами 3 и 7. Найдите радиус окружности, касающейся каждой из этих окружностей.
р 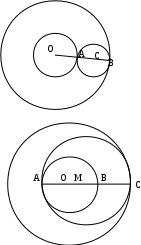ешение:

1. АВ=ОВ-ОА=7-3=4

CВ= АВ=2.


АС=АО+ОС==3+7=10,

МС= АС=5.


Ответ: 2 или 5.

2. На плоскости имеются две окружности. Чему равен радиус окружности, касающейся данных окружностей и имеющей центр на прямой, проходящей через их центры, если радиусы данных окружностей и расстояния между их центрами соответственно равны: а) 1,3,5; б) 5,2,1; в) 3,4,5? Сколько решений имеет задача?
Решение:

В каждом пункте может быть 4 возможных расположения третьей окружности относительно двух данных, так как центры данных окружностей не совпадают.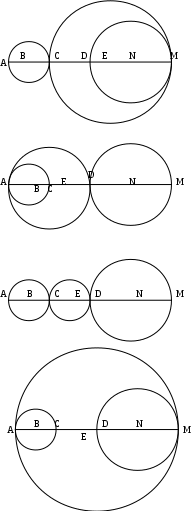

пусть В-центр окружности с радиусом 1,

N-центр окружности с радиусом 3,

Е-радиус искомой окружности.

Тогда

AB=BC=1,ND=MN=3,BN=5.

1) BN=BC+CN,

CN=5-1=4,

CM=CN+NM=4+3=7

EM= CM=3,5.
2) BN=BC+CD+DN,

CD=BN-BC-DN=5-1-3=1,

AD=AC+CD=2+1=3,

ED= AD=1,5.

3) BM=BC+CD+DN,

CD=BM-BC-DN=5-1-3=1

ED= CD=0,5

4) AM=AB+BN+NM=1+5+3=9

EM= AM=4,5.

Б )

Пусть A-центр окружности

с радиусом 2,

B-центр окружности

с радиусом 5,

C-искомой окружности.

тогда

AN=AM=2,BD=BK=5,AB=1.

1) CK=?

DN=DB-BA-AN=5-1-2=2,

KM=KD-DN-NM=10-2-4=4,

CK= KM=2.

2) CD=?

DN=DB-BA-AN=5-1-2=2,

CD= DN=1.

3) CK=?

DN=DB-BA-AN=5-1-2=2,

KN=DK-DN=10-2=8,

CK= KN=4.
4) CM=?

DM=DN+NM=2+4=6,

CM= 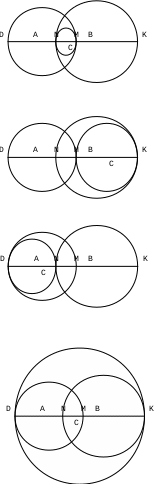DM=3.



Пусть A-центр окружности

с радиусом 3,

B-центр окружности

с радиусом 4,

C-искомой окружности.

Тогда

AD=AM=3,BN=BK=4,AB=5.

1) CN=?

BM=AB-AM=5-3=2,

AN=AB-BN=5-4=1,

MN=AB-BM-AN=5-2-1=2,

CN= MN=1.

2) CK=?

KM=KN-NM=8-2=6,

CK= KM=3.

3) CD=?

CD=DM-NM=6-2=4,

CD= DM=2.

4) CK=?

DK=DM+NK-NM=6+8-2=12

CD= DK=6.
Ответ: а) 3,5 или 0,5 или 1,5 или 4,5;

Б) 1 или 2 или 3 или 4;

В) 1 или 2 или 3 или 6.

3. В вершинах треугольника расположены центры трёх попарно касающихся окружностей. Найдите радиусы этих окружностей, если стороны треугольника равны 5,6,7. Сколько решений имеет задача?

РЕШЕНИЕ:

Точки касания располагаются на прямых,

соединяющих центры, то есть на АВ, ВС и АС.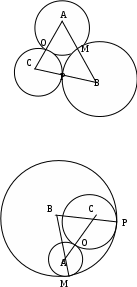

1. 
   пусть АС=5, ВС=6, АВ=7
   

АО=х, тогда

ОС=СР=5-х, ВМ=РВ=7-х, но

СР+РВ=6, 5-х+7-х=6

АО=х=3,СР=5-х=2,РВ=7-х=4.

2. 
   пусть АС=5, ВС=7, АВ=6
   

ВМ=х, тогда

АМ=АО=х-6, СО=СР=х-7, но

СО+АО=5, х-7+х-6=5

ВМ=х=9,АО=х-6=3,РВ=Х-7=2.

3. 
   пусть АС=7, ВС=6, АВ=5
   

ВМ=х, тогда

АМ=АО=х-5, СО=СР=х-6, но

СО+АО=7,х-7+х-6=7

ВМ=х=9,АО=х-5=4, РВ=Х-6=3.

4. 
   пусть АС=6, ВС=5, АВ=7
   

ВМ=х, тогда

АМ=АО=х-7, СО=СР=х-5, но

СО+АО=6,х-7+х-5=6

ВМ=х=9,АО=х-7=2, РВ=Х-5=4.
ОТВЕТ: 2,3,4 или 2,3,9 или 3,4,9 или 2,4,9.

домашнее задание.
1. Даны две окружности с общим центром и радиусами к и К. (к ). Найдите радиус окружности, касающейся каждой из этих окружностей. (Решение аналогично решению задачи в классе.)

Ответ: или .

2 . На прямой расположены точки А,В,С и D, при чём АВ = 2,

CD = 3. Отрезки АС и BD являются диаметрами двух окружностей. Найдите расстояние между центрами этих окружностей

Решение:

AD=AB+CB+CD=5+CB

A 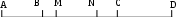M=MC B BN=ND

AD=AM+MN+ND=2NM+BC

5+CB=2NM+BC

MN=2,5

2 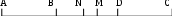) AD=AB+BD=2+BD

AM=MC B BN=ND

AD=AM+ND-NM=MC+BN-NM=MD+3+BN-NM=

=3+BD-2NM

2+BD =3+BD-2NM

MN= .

Ответ: 2,5 или .


4 занятие(четырехугольники)
1. Даны три точки А, В, С, не лежащие на од­ной прямой. Построить точку М такую, чтобы точки А, В, С, М были вершинами паралле­лограмма.

параметром в данной задаче является неопределенность, какой из трех отрезков: АВ, АС или ВС принять за диагональ параллелограмма.

Построение: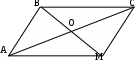

3. 
   АС
   
4. 
   О –середина АС
   
5. 
   ВО
   
6. 
   М: М ВО, ВО=ВМ
   
7. 
   АВ, АМ, ВС, СМ.
   

Четырехугольник АВСМ параллелограмм по определению. Построение в двух других случаях аналогично первому.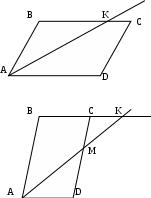
2. Биссектриса угла А параллелограмма АВСD пересекает сторону BC в точке К. Найдите периметр этого параллелограмма, если ВК = 15см КС = 9см.
решение:

треугольник АВК равнобедренный из равенства

углов при основании. Следовательно, АВ=ВК=15см.

1. 
   пусть точка К находится между точками В и С,
   

тогда ВС=ВК+КС=15+9=24(см)

Р=2(АВ+ВС)=2(15+24)=78(см)

2. 
   пусть точка К находится вне отрезка ВС,
   

тогда ВС=ВК-КС=15-9=6(см)

Р=2(АВ+ВС)=2(15+6)=42(см)

Ответ: 78см или 42см.
3. О параллелограмме ABCD известно что угол ABD равен 40^о и что центры окружностей, описанных около треугольников ABC и CDA, лежат на диагонали BD. Найдите угол DBC.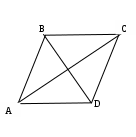




решение:

так как центры окружностей,

описанных около треугольников ABC и CDA,

лежат на диагонали BD, то точки

пересечения серединных перпендикуляров

лежат на BD, получаем, что BD АС,

следовательно, ABCD - ромб или центры окружностей лежат в точке пересечения диагоналей, и тогда ABCD - прямоугольник.

Если ромб, то угол DBC=40⁰, так как диагонали ромба являются биссектрисами его углов.

Если прямоугольник, то угол DBC=50⁰, так как угол АВС=90⁰.

Ответ: 40⁰ или 50⁰.
Домашняя работа.
1. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7см и 14см.

(ответ: 70см или 42см).

2. От параллелограмма с помощью прямой, пересекающей две его противоположные стороны, отрезали ромб. От оставшегося параллелограмма таким же образом вновь отрезали ромб. И от вновь оставшегося параллелограмма опять отрезали ромб. В результате остался параллелограмм со сторонами 1 и 2. Найдите стороны исходного параллелограмма.

1.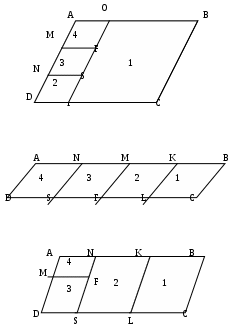 
   п усть AO=1, AM=2.
   

MF=MN=DN=DP=AO=1

AD=AM+MN+DN=2+1+1=4=OP=OB

AB=AO+OB=1+4=5

2) пусть AO=2, AM=1.

MF=MN=DN=DP=AO=2

AD=AM+MN+DN=1+2+2=5=OP=OB

AB=AO+OB=2+5=7
3) пусть AN=2, AD=1.

MN=MK=KB=CB=AD=1

AB=AN+MN+MK+KB=2+1+1+1=5

4) пусть AN=1, AD=2.

MN=MK=KB=CB=AD=2

AB=AN+MN+MK+KB=1+2+2+2=7

5. 
   пусть AN=1, AM=2.
   

MF=MD=DS=AN=1

AD=AM+MD=2+1=3=NS=NK=KB

AB=AN+NK+KB=1+3+3=7

5. 
   пусть AN=2, AM=1.
   

MF=MD=DS=AN=2

AD=AM+MD=1+2=3=NS=NK=KB

AB=AN+NK+KB=2+3+3=8

Ответ: 4 и 5, или 5 и 7, или 1 и 5, или 2 и 7, или 3 и 7, или3 и 8.

5 занятие(четырехугольники)
1. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см.?

решение:

треугольники АКМ и РОВ- равнобедренные,

из равенства углов при основании.

С 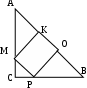ледовательно АК=КМ и ОР=ОВ.

1. 
   пусть , тогда
   

МК=5х, а КО=2х.

АВ=АК+КО+ОВ=МК+КО+ОВ=5х+2х+5х

45=12х

х=3,75

МК=5х=18,75 а КО=2х=7.5

2. 
   пусть , тогда
   

МК=2х, а КО=5х.

АВ=АК+КО+ОВ=МК+КО+ОВ=2х+5х+2х

45=9х

х=5

МК=5х=25 а КО=2х=10

Ответ: 18,75 и 7.5, или 25 и 10.
2. Диагональ трапеции делит её на два равнобедренных треугольника. Угол при основании одного из этих треугольников равен 40^о. найти углы трапеции.

Решение:

Очевидно, что в треугольнике ВСК ВК-основание,

Так как угол С-тупой, в треугольнике АВК

все углы острые, следовательно

можно рассмотреть 3 случая: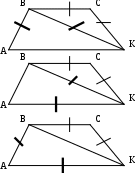

1. 
   А В=ВК
   

тогда КВС= СКВ=40^о, С=100⁰,

ВКА= КВС как внутренние накрест лежащие,

ВКА= ВАК=40⁰, АВК=100⁰.

А=40⁰, В=140⁰, С=100⁰, К=80⁰.

2) ВК=АК, тогда КВС= СКВ=40^о, С=100⁰,

ВКА= КВС как внутренние накрест лежащие,

АВК= ВАК=70⁰.

А=70⁰, В=110⁰, С=100⁰, К=80⁰.

2. 
   АВ=АК, КВС= СКВ=40^о, С=100⁰,
   

ВКА= КВС как внутренние накрест лежащие,

тогда АВК= ВКА=40⁰, ВАК=100⁰.

А=100⁰, В=80⁰, С=100⁰, К=80⁰.

Получился параллелограмм, а по условию дана

трапеция, значит такого случая быть не может.
Ещё одно решение получается, если рассмотреть трапецию, у которой при большем основании один угол острый, а другой – тупой.




ВС=ВК, АВ=ВК. А=40⁰, тогда ВКА=40⁰

ВКА= КВС как внутренние накрест лежащие,

ВКС= С=70⁰.

А=40⁰, В=140⁰, С=70⁰, К=110⁰.
Ответ: 40⁰, 140⁰, 100⁰, 80⁰ или 70⁰, 110⁰, 100⁰, 80⁰ или 40⁰, 140⁰, 70⁰, 110⁰.

3. Биссектрисы углов А и D параллелограмма АВСD пересекают прямую ВС в точках Е и F соответственно. Найдите стороны парал­лелограмма, если его периметр равен p и известно, что .

Решение: 1.рассмотрим сначала случай, когда точка пересечения биссектрис лежит внутри параллелограмма.



AB=BE=CF=CD, так как треугольники ABE и FDC равнобедренные,

AD=CD как стороны

параллелограмма, BAD= BEA

Как внутренние

Накрест лежащие при

BC||AB и AC биссектриса.

Пусть EF=х

=AB+BE+FC-EF

=3BE-x=

Отсюда x= * ^.