AB=BE= BC=BE+CF-x= . .
2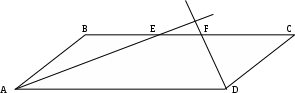 . теперь рассмотрим случай, когда точка пересечения биссектрис лежит вне параллелограмма. . теперь рассмотрим случай, когда точка пересечения биссектрис лежит вне параллелограмма.
Здесь решение аналогично предыдущему: AB=BE=CF=CD аналогично.
Пусть EF=x
 =AB+BE+FC+EF =AB+BE+FC+EF
 =3BE+x= =3BE+x= 
Отсюда х=
AB=BE=
BC=BE+CF+x= . .
Ответ: если точка пересечения биссектрис лежит вне параллелограмма, то AB= , BC= , BC= ; ;
если точка пересечения биссектрис - внутри параллелограмма, то AB= , BC= , BC=
Домашняя работа:
1. отношение углов А и В, прилежащих к боковой стороне трапеции АВСК, равно 2:3. диагональ АС делит трапецию на два равнобедренных треугольника. Найти углы трапеции.
Р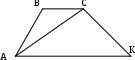 ЕШЕНИЕ: ЕШЕНИЕ:
 , тогда , тогда  А=2х, А=2х,  В=3х. В=3х.
так как сумма внутренних односторонних углов
равна 1800, то 2х+3х=1800, х=360, тогда
 А=720, а А=720, а  В=1080. В=1080.
 ВАС= ВАС= ВСА=360, и ВСА=360, и  САК=360. САК=360.
АС=СК  СКА= СКА= САК=360, САК=360,  АСК=1080 АСК=1080
 А=720, А=720,  В=1080, В=1080,  С=1440, С=1440,  К=360. К=360.
АС=АК  АСК= АСК= АКС=720, АКС=720,
 А=720, А=720,  В=1080, В=1080,  С=1080, С=1080,  К=720. К=720.
в случае, когда СК=АК получается параллелограмм.
Ответ: 720, 1080, 1440, 360 или 720, 1080, 1080, 720.
2. Боковые стороны трапеции равны 17см и 10см, найти основания трапеции, если известно, что её высота равна 8см, а средняя линия 30см.
Решение:
р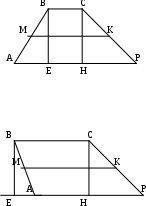 ассмотрим ассмотрим  АВЕ и АВЕ и СРН. СРН.
Прямоугольные. По теореме Пифагора в  АВЕ: АВЕ:
АЕ2=100-64=36,
АЕ=6.
По теореме Пифагора в  СРН: СРН:
РН2=289-64=225,
АЕ=15.
ВС=ЕН, так как ВСНЕ- параллелограмм
(противолежащие стороны параллельны).
1) МК= (ВС+АР)= (ВС+АР)=  (ВС+АЕ+ЕН+НР)= (ВС+АЕ+ЕН+НР)=
= (ВС+АЕ+ВС+НР)= (ВС+АЕ+ВС+НР)= (2ВС+6+15)=30 (2ВС+6+15)=30
ВС=19,5СМ
АР=40,5СМ
2) МК= (ВС+АР)= (ВС+АР)=  (ВС+ЕН+НР-АЕ)= (ВС+ЕН+НР-АЕ)=
= (ВС+ВС+НР-АЕ)= (ВС+ВС+НР-АЕ)= (2ВС-6+15)=30 (2ВС-6+15)=30
ВС=25,5СМ
АР=34,5СМ
Ответ: 25,5СМ и 34,5СМ или 19,5СМ и 40,5СМ.
6 занятие( окружность и т Пифагора)
1. Две стороны прямоугольного треугольника равны 3м. и 4м. Найти третью сторону.
1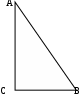 ) пусть АС=4м, ВС=3м. ) пусть АС=4м, ВС=3м.
по теореме Пифагора в треугольнике АВС:
АВ2=16+9=25
АВ=5
2) пусть АВ=4м, ВС=3м.
по теореме Пифагора в треугольнике АВС:
АС2=16-9=7
АС=
Ответ:5 или 
2. Расстояние между центрами двух окружностей равно 10к. Одна из окружностей имеет радиус 5к, вторая — 6к. Прямая пересекает меньшую окружность в точках А и В и касается большей в точке С. Найдите длину хорды АВ, если известно, что АВ = 2 • ВС.
р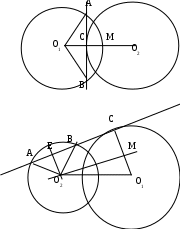 ешение: ешение:
О1О=10к,О1М=5к, О2С=6к
Следовательно, СМ=1к,
а О1С=4к
по теореме Пифагора
в треугольнике О1АС:
АС2=25к-16к=9к,
АС=3к,
АВ=6к.
2.пусть АВ=2х
по теореме Пифагора
в треугольнике О2ЕВ
О2Е2=25к2-х2
О2Е=
по теореме Пифагора
в треугольнике О1МО2
О1М2=100к2-4х2
О1М=2
О1М=2О2Е
СО1=6к=СМ+МО1=ЕО2+МО1
6к= ЕО2+МО1=3О2Е
О2Е=2к

х= к к
АВ=2 к. к.
Ответ: 2 к или 6к. к или 6к.
3. Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки длины 8 и 18. Найдите основания трапеции.
решение:
NC=CE=8, из равенства по гипотенузе и
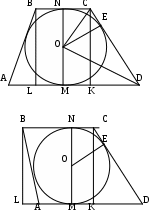 катету треугольников NOC и EOC. катету треугольников NOC и EOC.
ED=MD=18, из равенства по гипотенузе и
катету треугольников DOE и DOM.
KD=MD-МК=18-8=10,
По теореме Пифагора для треугольника СКD:
СК= r=12 r=12
AB=BN+AМ (также как СD=NC+MD)
BN+AМ+AB=60(так как 112-8-8-18-18=60),
Тогда AB=30.
По теореме Пифагора для треугольника АВL:
AL=
1.P=AB+BN+NC+CD+DM+ML+AL=
=30+BN+8+26+18+ML+18=112
ML=BN=6, BC=8+6=14, AD=18+6+18=42.
P=AB+BN+NC+CD+DM+ML-AL=30+BN+8+26+18+ML-18=112
ML=BN=24, BC=24+8=32, AD=24-18+18=24.
Ответ: 14 и 42 или 24 и 32.
Домашняя работа:
1. Две стороны треугольника равны 25см и 30см. Найти третью сторону, если высота, проведённая к ней равна 24см.
Р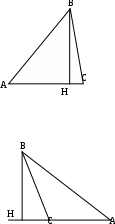 ЕШЕНИЕ: ЕШЕНИЕ:
АВ=30см, ВС=25см, ВН=24см.
Треугольники АВН и ВСН – прямоугольные.
По теореме Пифагора в  АВН: АВН:
АН2=900-576=324
АН=18(см)
По теореме Пифагора в  ВСН: ВСН:
СН2=625-576=49
СН=7(см).
Поскольку не сказано, остроугольный или тупоугольный треугольник, то можно рассмотреть 2 случая:
остроугольный:
АС=АН+СН=18+7=25(см).
тупоугольный:
АС=АН-СН=18-7=11(см).
Ответ: 25см или 11см.
7 занятие( окружность и т Пифагора)
1. Длины соседних сторон вписанного в окружность четырехугольника отличаются на 1. Длина наименьшей из них так же равна I. Найдите радиус окружности.
р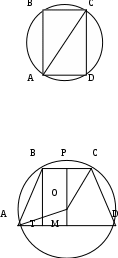 ешение: ешение:
1) ВС=1, тогда АВ=ВС=2, АD=1
АС=
ОС=
2) ВС=1, тогда АВ=ВС=2, АD=3
к-радиус
ВТ= , пусть ОМ=а , пусть ОМ=а
По теореме Пифагора из тр-ка АОМ
К=
Из тр-ка ОРС:
К=
2.25=0.25+3-2 а а
а= , к= , к=
ответ: 
2. Дан отрезок длины 20. Три окружности с радиусами 4 имеют центры в концах отрезка или в его середине. Найдите радиус четвертой окружности, касающейся трех данных.
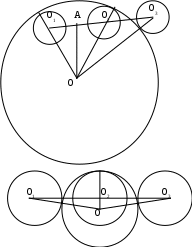
1. решение:
к-искомый радиус.
 ОО1О2-равнобедренный, ОО1О2-равнобедренный,
с боковыми сторонами, равными (к-4),
тогда высота ОА является
также и медианой.
По теореме Пифагора:
Из  АОО2 АОО2
ОА2=(К-4)2-25
Из  АОО3 АОО3
ОА2=(К+4)2-225
-8К-25=8К-225, 16К=200, К=12.5
2. пусть к- искомый радиус, ОО2=а, тогда
к=4+а,
по теореме Пифагора для треугольника ОО2О3
а2=((а+4)+4)2-100
16а=36,
а=2.25,
к=6.25.
Ответ: 6,25 или 12,5.
Домашняя работа:
1. Найти высоту равнобедренного треугольника с основанием а и радиусом описанной окружности R.
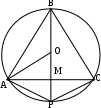
Решение.
Поскольку вершина, противолежащая основанию,
может лежать на одной из двух дуг описанной
окружности (т.е. в разных полуплоскостях
относительно прямой, содержащей основание
треугольника), то задача будет иметь
два различных решения:
1) Если угол, противолежащий основанию, острый ( В), то расстояние от центра окружности до основания ОМ=Н—R, где Н — высота ВМ, проведенная к основанию. Тогда по теореме Пифагора для треугольника АОМ: АО2=R2=( В), то расстояние от центра окружности до основания ОМ=Н—R, где Н — высота ВМ, проведенная к основанию. Тогда по теореме Пифагора для треугольника АОМ: АО2=R2=( )2+(H-R)2, откуда получаем квадратное уравнение относительно H: H2-2HR+ )2+(H-R)2, откуда получаем квадратное уравнение относительно H: H2-2HR+ =0. Корни этого уравнения числа Н1,2=R± =0. Корни этого уравнения числа Н1,2=R±  . .
Если же угол, противолежащий основанию, тупой( Р), то расстояние от центра окружности до основания Р), то расстояние от центра окружности до основания
равно ОМ=R-Н, а следовательно, R2 = ( )2+(R-H)2 )2+(R-H)2
что приведет к тому же самому квадратному уравнению. Таким образом, квадратное уравнение само предусмотрело два различных решения этой задачи.
Ответ: R±  . .
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.