Деревянные конструкции. Дисциплина Конструкции из дерева и пластмасс Модуль Деревянные конструкции
 Скачать 218.28 Kb. Скачать 218.28 Kb.
|
|
Дисциплина: «Конструкции из дерева и пластмасс» Модуль 2. Деревянные конструкции Практическое задание № 2. Расчёт деревянной балки перекрытия Задание Результаты выполнения задания представляются в расчётно-пояснительной записке объёмом 5-10 листов. Выполнить расчёт деревянной балки чердачного перекрытия над вторым этажом для перекрытия помещения спальни площадью 19,47м2 индивидуального жилого дома. 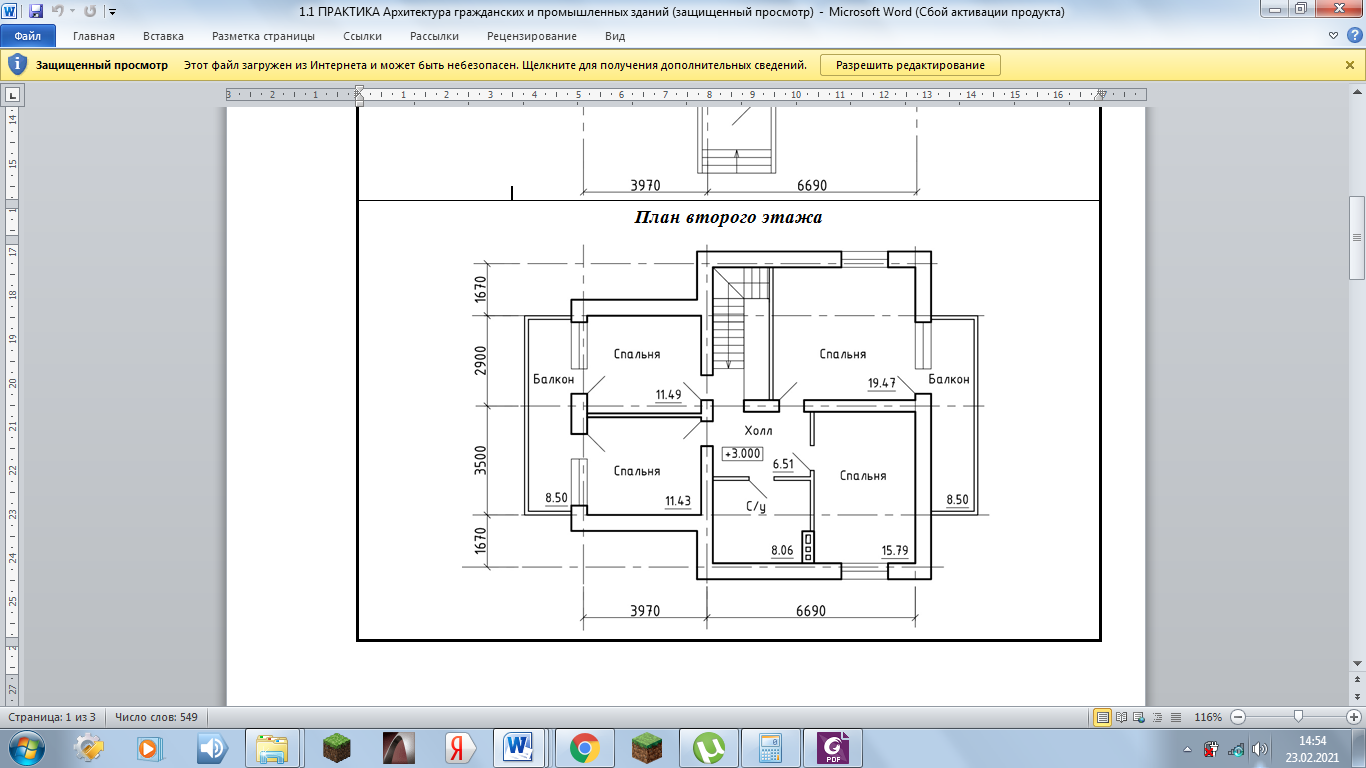 Таблица 1 Исходные данные для расчёта
Расчёт выполнен в соответствии с СП 64.13330.2017. Деревянные конструкции [2]. Исходные данные. Требуется рассчитать балку чердачного перекрытия над вторым этажом в индивидуальном доме для перекрытия помещения спальни площадью 19,47м2. Материал – лиственница 2 сорта. Срок службы конструкций – 50 лет. Балки цельного сечения (не клееные). Шаг балок s – 700 мм; Длина пролёта (2900+1670) = 4,57 м (4570 мм); Пропитка антипиренами под давлением - не предусмотрена. Расчётная нагрузка на 1 м2 перекрытия Р– 150 кг/м2 = 1,5 кН/м2; 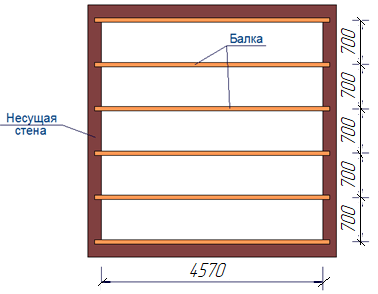 Расчёт по 1 группе предельных состояний. Расчёт по прочности. 1) Расчётная схема Так как балка опирается на две стены, т.е. она шарнирно опёрта и нагружена равномерно-распределённой нагрузкой, то расчётная схема будет выглядеть следующим образом: 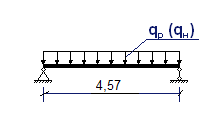 Погонная нагрузка на балку – qр = Р·s=1,5·0,7 = 1,05 кН/м. Нормативная нагрузка на перекрытие – 1,5/1,1 = 1,36 кН/м2; на балку - qн = 1,36·0,7 = 0,952 кН/м. 2) Расчёт по прочности Определяем максимальный изгибающий момент для данной расчётной схемы: Мmax= qp·l2/8 = 1,05·4,572/8 = 0,60 кН·м=600000 Н·мм, где qp - расчетная нагрузка на балку; l - длина пролёта. Расчётное сопротивление древесины определяется по формуле: Rр = Rи·mдл·mп·mв·mт·mсc = 19,5·0,53·1,2·1·1·0,9 = 11,16 МПа = 11,16 Н/мм2 Rи –расчётное сопротивление для сосны, ели и лиственницы при влажности 12% согласно п. 1, а таблицы 3 СП 64 [2]. mдл = 0,53 – коэффициент длительной прочности, принимаемый в соответствии с п.6.1 [2], вводится в случае, когда постоянные и временный длительные нагрузки превышают 80% суммарного напряжения от всех нагрузок. mп = 1,2 – коэффициент перехода для других пород древесины, в данном случае принятый для лиственницы (таблица 5 [2]). mв = 1 – коэффициент условий работы (таблица 9 [2]), режим эксплуатации сухой. mт = 1 – температурный коэффициент, принят 1 при условии, что температура не превышает +35 °С. mсс = 0,9 - коэффициент срока службы древесины, подбирается в зависимости от того, сколько времени вы собираетесь эксплуатировать конструкции (таблица 13 [2]). Определение требуемого момента сопротивления деревянной балки: Wтреб = Mmax/Rр = 600000/11,16 = 53763,44 мм3, Определение сечения балки. Назначаем ширину сечения балки 50 мм с учетом имеющейся номенклатуры пиломатериалов, тогда минимальная высота балки определяется по следующей формуле: h = √(6Wтреб/b) = √(6·53763,44/50) = 80,32 мм. Формула подобрана из условия W = b·h2/6. Необходимо подобрать высоту балки, так, чтобы она была не менее 80,32 мм, и имелась в номенклатуре пиломатериалов. В номенклатуре пиломатериалов назначаем балку высотой 100 мм. Получившийся результат является удовлетворительным, так как отсутствует перерасход материала. Принимаем для сечения балки брус bxh = 50x100 мм. 3) Расчёт по второй группе предельных состояний. Определяем прогиб принятой балки по формуле соответствующей принятой расчётной схеме: f = (5·qн·l4)/(384·E·J) = (5·0,952·45704)/(384·10000·4166666,67) = 129,76 мм; где qн = 0,952 кН/м =0,952 Н/мм – нормативная нагрузка на балку; l = 4570 мм – длина элемента; Е = 10000 МПа – модуль упругости. Принимается равным в соответствии с СП 64.13330.2017 Деревянные конструкции вдоль волокон 10000 МПа и 400 МПа поперёк волокон. J = b·h3/12 = 50·1003/12 = 4166666,67 мм4 – момент инерции для балки прямоугольного сечения. Определяем предельно допустимый прогиб балки: fmax = l·/200 = 4570/200 = 22,85 мм. Предельный прогиб определяется по приложению Д.2 СП 20.13330.2016 Нагрузки и воздействия [4], как для междуэтажных перекрытий. Для того чтобы балка удовлетворяла требованиям расчёта по II группе предельных состояний, т.е. требованиям достаточной жёсткости, должно соблюдаться условие: f < fmax Сравниваем прогиб балки с предельно допустимым: f = 129,76 см fmax = 22,85 мм. Условие f < fmax не выполняется, поэтому увеличиваем высоту сечения, принимаем сечение 50х150 мм. Производим расчёт ещё раз. J = b·h3/12 = 50·1503/12 = 14062500 мм4 – момент инерции для балки прямоугольного сечения. f = (5·qн·l4)/(384·E·J) = (5·0,952·45704)/(384·10000·14062500) = 38,44 мм; f = 38,44 см fmax = 22,85 мм, условие не выполняется, поэтому увеличиваем высоту сечения, принимаем сечение 50х200 мм. Производим расчёт ещё раз. J = b·h3/12 = 50·2003/12 = 33333333,33 мм4 – момент инерции для балки прямоугольного сечения. f = (5·qн·l4)/(384·E·J) = (5·0,952·45704)/(384·10000·33333333,33) = 16,22 мм; f = 16,22 см fmax = 22,85 мм, условие выполняется. Вывод: балка сечением bxh = 50x200 мм удовлетворяет условиям по прочности и жёсткости (прогибу). Перечень рекомендуемой литературы Волосухин, В.А. Строительные конструкции: учебник для студентов вузов / В.А. Волосухин, С.И. Евтушенко, Т.Н. Меркулова. – 4-е изд., перераб. и доп. – Ростов-на-Дону : Феникс, 2013. – 555 с. : ил., схем., табл. – (Высшее образование). – Режим доступа: по подписке. – URL: https://biblioclub.ru/index.php?page=book&id=271492 2. СП 64.13330.2017 Деревянные конструкции. Актуализированная редакция СНиП II-25-80 (с Изменениями N 1, 2). – М.: Стандартинформ, 2019. 3. ГОСТ 8486-86 Пиломатериалы хвойных пород. Технические условия 4. СП 20.13330.2016 Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07-85** [Текст]/ Минстрой России. 2016.- 88с. 5. ГОСТ 24454-80* Пиломатериалы хвойных пород. Размеры. |
