контрольная. Дисконтированием
 Скачать 46.11 Kb.
|
|
ВАРИАНТ № 2 Вопрос: Дисконтирование по простым процентным ставкам. Наращение по учетной ставке? В практике часто приходится решать задачу обратную наращению процентов, когда по заданной сумме S, соответствующей концу финансовой операции, требуется найти исходную сумму P. Расчет P по S называется дисконтированием суммы S. Величину P, найденную дисконтированием, называют современной величиной (текущей стоимостью) суммы S. Проценты в виде разности 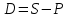 называют дисконтом или скидкой. Процесс начисления и удержания процентов вперёд (в виде дисконта) называют учетом. Дисконт как скидка с конечной суммы долга может определяться через процентную ставку или в виде абсолютной величины.Таким образом, в практике используются два принципа расчета процентов: 1. путем наращения суммы ссуды и 2. Устанавливая скидку с конечной суммы долга. В большинстве случаев фактор времени учитывается в финансовых контрактах именно с помощью дисконтирования. Величина P эквивалентна сумме S в том смысле, что через определенный период времени и при заданной ставке процентов она в результате наращения станет равной S. Поэтому операцию дисконтирования называют также приведением. Но понятие приведения шире, чем дисконтирование. Приведение – это определение любой стоимостной величины на некоторый момент времени. Если некоторая сумма приводится к более ранней дате, чем текущая, то применяется дисконтирование, если же речь идет о более поздней дате, то – наращение. Известны два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. Математическое дисконтирование. Этот вид дисконтирования представляет собой решение задачи, обратной наращению первоначальной ссуды. Если в прямой задаче: 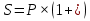 (1)то в обратной: 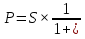 (2)Дробь в правой части равенства при величине S называется дисконтным множителем. Этот множитель показывает какую долю составляет первоначальная сумма ссуды в окончательной величине долга. Дисконт суммы S равен: 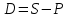(3)Банковский или коммерческий учет. Операция учета (учета векселей) заключается в том, что банк до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца (являющегося кредиторов) по цене ниже той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает (учитывает) его с дисконтом. Для расчета процентов при учете векселей применяется учетная ставка, которую обозначим символом d. По определению, простая годовая учетная ставка находится как 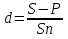 (4)Размер дисконта или учета, удерживаемого банком, равен 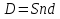 (5)откуда 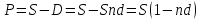 (6) Множитель (1-nd) называется дисконтным множителем. Срок n измеряет период времени от момента учета векселя до даты его погашения в годах. Дисконтирование по учетной ставке производится чаще всего при условии, что год равен 360 дням. Наращение по учетной ставке. Учетная ставка может использоваться для наращения, т.е. для расчета S по P. В этом случае из формулы (6) следует, что 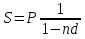 (7)Задача № 1: В конце третьего года величина вклада стала равной 280 денежных единиц (д.е.). Оцените величину годовой процентной ставки, по которой начислялись проценты в сумме 30 д.е. за каждый год. Дано : n = 3, S = 280, I1 = I2 = I3, I = 90 (3 * 30) Найти : i Решение: Одинаковая сумма процентов каждый год (при неизменной ставке процентов) говорит о применении простой процентной ставки (т.е. о начислении процентов только на сумму вклада). Определим первоначальную величину вклада. Формула наращенной суммы с использованием процентов записывается в следующем виде : S = P + I где S – наращенная сумма P – первоначальная сумма I – сумма процентов Отсюда : P = S - I P = 280 – 90 = 190 д.е. Определение уровня простой процентной ставки по остальным параметрам сделки производится по следующей формуле : i = 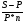 где i – процентная ставка, выраженная десятичной дробью, S – наращенная сумма, P – вкладываемая сумма, n – срок ссуды в годах. i = 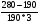 = 0,1579 или 15,79%Ответ : величина годовой процентной ставки равна 15,79%. Задача № 2: В конце второго года величина вклада стала равной 250 денежных единиц (д.е.). Оцените величину годовой процентной ставки, по которой начислялись проценты в сумме 30 д.е. за каждый год. Дано : n = 2, S = 250, I1 = I2 = I3, I = 90 (3 * 30) Найти : i Решение: Одинаковая сумма процентов каждый год (при неизменной ставке процентов) говорит о применении простой процентной ставки (т.е. о начислении процентов только на сумму вклада). Определим первоначальную величину вклада. Формула наращенной суммы с использованием процентов записывается в следующем виде : S = P + I где S – наращенная сумма P – первоначальная сумма I – сумма процентов Отсюда : P = S - I P = 250 – 90 = 160 д.е. Определение уровня простой процентной ставки по остальным параметрам сделки производится по следующей формуле : i = 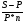где i – процентная ставка, выраженная десятичной дробью, S – наращенная сумма, P – вкладываемая сумма, n – срок ссуды в годах. i = 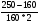 = 0,2813 или 28,13%Ответ : величина годовой процентной ставки равна 28,13%. Задача № 3: Рассчитать сумму выплаты по депозиту в размере 20 000 руб., помещенному на 1 год 14% годовых с ежеквартальным начислением процентов. Решение: 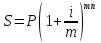 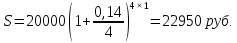 Ответ: Сумма выплаты составит 22 950 рублей. Задача № 4: Вклад в размере 5000 руб. положен в банк на депозит 11 марта под 14% годовых по схеме сложных процентов. Какую сумму вкладчик получит 20 августа? (точные проценты с приближенным числом дней) Решение: 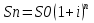 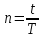 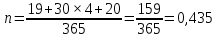 (считается, что в месяце 30 дней, в году – 365) 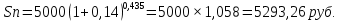 Ответ: Вкладчик получит 20 августа 5293,26 рубля. Задача № 5 Инвестиционное предложение состоит в фиксированной норме прибыли из расчета 8% годовых в течение 5 лет. Давайте рассмотрим, какую сумму необходимо положить сейчас, чтобы по истечении указанного срока накопить 2 000 ф.ст. Решение: Имеем Sr=2 000, i=8 и n=5. Следовательно, текущую стоимость можно вычислить следующим образом: 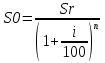 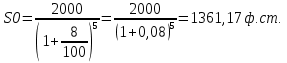 Ответ: Итак, сейчас необходимо вложить 1361,17 ф.ст. чтобы через 5 лет эта сумма превратилась в 2000 ф.ст. Задача № 6: Определить сумму вложения, необходимую сейчас, с тем, чтобы накопить сумму в 1 000 ф.ст. по окончании заданных периодов:
Решение: а)  b) 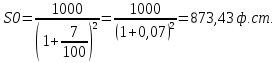 c)  Ответ: а) Сумма вложения равна 821,92 ф.ст. b) Сумма вложения равна 873,43 ф.ст. c) Сумма вложения равна 564,47 ф.ст. Задача № 7: Сумма 50 000 руб. выдается в ссуду на полгода по годовой учетной ставке 30%. На какую сумму следует выдать вексель? Дано : P = 50000, n = 0,5, d = 0,30 Найти : S Решение: Используем формулу наращенной суммы при антисипативном методе начисления процентов : 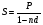 где S – наращенная сумма, P – сумма капитала, предоставляемого в ссуду, d - простая учетная ставка n – срок ссуды в годах 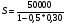 = 58823,52 руб. Ответ : следует выдать вексель на сумму 58823,52 руб. Задача № 8: Определить номинальную ставку процентов для финансовой операции. Банк выдает кредит под 30% годовых с уплатой процентов за год вперед, а сумма кредита возвращается через год. Годовой уровень инфляции составил 30%. Дано : i = 0,30, n = 1, h = 0,30 Найти : iномин Решение: Размер суммы процента можно определить по формуле : I = P * n * i Где P – сумма капитала, предоставляемого в кредит, I – величина начисленных процентов, n – срок ссуды в годах, i – процентная ставка, выраженная десятичной дробью I = P * 1 * 0,3 = 0,3Р Полученная в начале срока сумма равна : Р – 0,3Р = 0,7Р В конце срока получаем сумму, равную Р. Определение уровня простой процентной ставки по остальным параметрам сделки производится по следующей формуле : i = 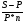где i – процентная ставка, выраженная десятичной дробью, S – наращенная сумма, P – первоначальная сумма, n – срок ссуды в годах. iномин = 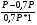 = 0,4286 или 42,86%СПРАВОЧНО найдем реальную ставку процентов для финансовой операции. Из формулы Фишера при инфляции реальная доходность определяется по формуле : 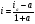 где i - безинфляционная ставка, отражающая реальную доходность операции ia – номинальная процентная ставка a – уровень инфляции. 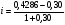 = 0,0989 или 9,89%Ответ : номинальная ставка процентов для финансовой операции равна 42,86%. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
|