Пример 3. Пусть V = {(a, b), (b, c, d), (c, a, d)}.
Чему равна проекция пр1 V?
Пример4. ПустьХ= {0,1}, Y= {a, b}. НайтиХ * Y, Y*X, X2, X*Y*X.
X*Y={(0,a),(0,b),(1,a),(1,b)}.
Y*X= {(a,0),(a,1),(b,0),(b,1)}.
Таким образом, X*Y ≠ Y*X.
Х2 = {(0,0), (0,1), (1,0), (1,1)}.
X*Y*X={(0, а, 0), (0, а, 1), (0, b, 0), (0, b, 1), (1, а, 0), (1,a,1),(1,b,0),(1,b,1)}.
Пример 5. Проиллюстрировать на конкретном примере утверждение: если
A 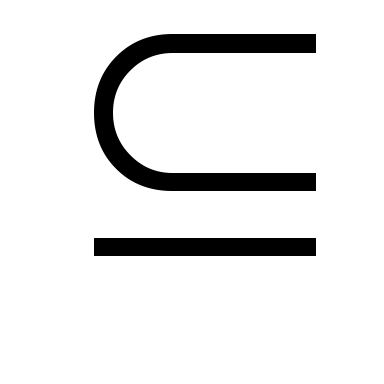 X B X B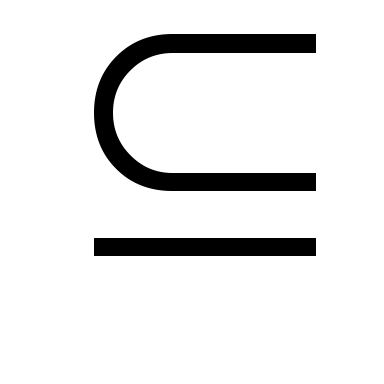 Y, то A*B Y, то A*B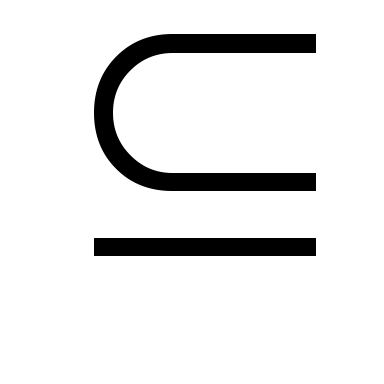 X*Y X*Y
Пусть А = {а}, Х= {а, b}, т.е. A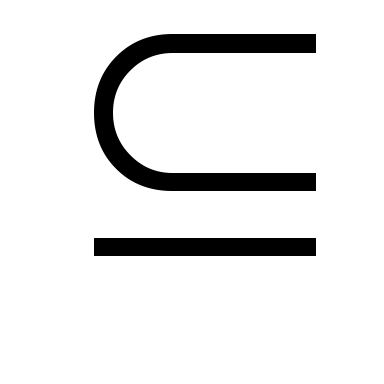 X и В = {1,2,}, Y= {1,2,3}, т.е. B X и В = {1,2,}, Y= {1,2,3}, т.е. B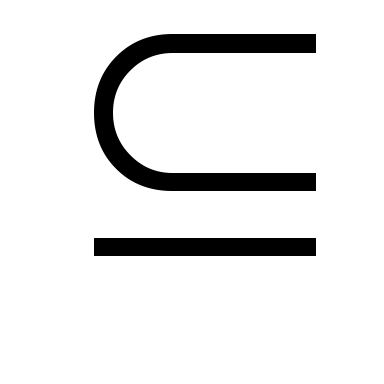 Y. Тогда: Y. Тогда:
А*В= {(a,1), (a,2)};
Х*Y= {(а, 1), (а, 2), (а, 3), (b,1), (b, 2), (b, 3)} = {(а, 1), (a, 2)}  {(а, 3), (b, 1), (b,2), (6, 3)} = [А * В] {(а, 3), (b, 1), (b,2), (6, 3)} = [А * В]  {(а, 3), (b, 1), (b, 2), (b, 3)} =X*Y. Таким образом, A*B {(а, 3), (b, 1), (b, 2), (b, 3)} =X*Y. Таким образом, A*B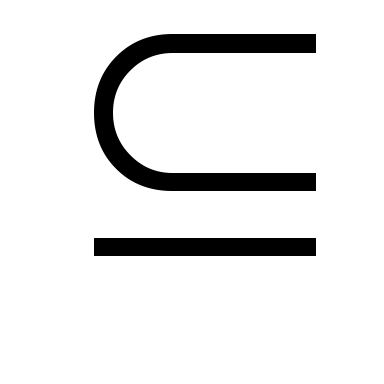 X*Y. X*Y.
Пример 6. Пусть А - алфавит, т.е. конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания, знаки операций и т.д.). Словом длины п в алфавите А (обозначается последовательностью из п символов без скобок и запятых) называют любой элемент множества An. В этом определении слово представлено как вектор. Множество всех слов в алфавите А - это множество А*:
A*=A1 A2 A2 A3 A3 ... ...
Пусть теперь алфавит A состоит из трех символов, например: А = {а, b, с}. Определить множество всех слов длины 1, 2, 3,4 в алфавите А.
• Множество всех слов длины 1 в алфавите , A = {а, b, с} -это множество всех слов из одной буквы алфавита А:
Al = {a,b,c}, \А1\ =3.
• Множество всех слов длины 2 в алфавите А - множество всех возможных двухбуквенных слов в алфавите А:
А2 =А*А = {аа, ab, ас, ba, bb, bс, ca, cb, ее}, \ А2\ = 9 = 32.
• Множество всех слов длины 3:
А3=А*А*А = {ааа, aab, aac, aba, ...,.ссс), \А3\ = 27 = 33.
• Множество всех слов длины 4:
А4=А*А*А*А = {аааа, aaab, aaac, aaba,...,сссс}, \А4\ =
= 81=34.
Очевидно, что мощность множества всех слов длины п в алфавите А равна мощности алфавита в степени п, т.е. | Ап \ = \ А\n
Пример 7. Пусть при сравнении пяти вариантов решений а, b, с, d, г по четырем характеристикам-критериям X, Y, Z, Uполучены следующие векторные оценки каждого варианта:
V = {(2, 3, 1, 2), (3, 3, 1, 2), (2, 2, 2, 2), (3, 2, 1, 2), (2,3,2,2)}.
Используя правило 1 сравнения векторов по предпочтению (см. с. 29), определить наилучшие векторные оценки и соответствующие им варианты решений.
В соответствии с правилом 1 выполним попарное сравнение векторных оценок из V. При сравнении первой векторной оценки со второй последняя оказывается не менее предпочтительной, а именно;
(2,3,1,2) ≤(3,3,1,2).
Поэтому дальнейшее сравнение первой векторной оценки со всеми другими можно не выполнять и далее ее не рассматривать. Оставшиеся векторные оценки:
V= {(3, 3, 1, 2), (2, 2, 2,2), (3,2, 1, 2), (2, 3, 2, 2)}.
В полученном списке V' векторных оценок первая сравнима по правилу 1 только с третьей этого списка: (3,3,1,2)≥(3,2,1,2).
Это позволяет отбросить третью векторную оценку в V' как менее предпочтительную. Новый список векторных оценок:
V" = {(3,3,1,2), (2, 2, 2,2), (2, 3,2, 2)}.
В новом списке V " сравнимыми по правилу 1 оказываются только последние две оценки:
(2,2,2,2)≤(2,3,2,2).
Оставшиеся две векторные оценки
V" = {(3,3, 1,2), (2, 3,2,2)}
несравнимы по правилу 1, т.е. никакой из них нельзя отдать предпочтение по данному правилу. Поэтому их следует признать лучшими среди векторных оценок исходного списка V.
Таким образом, наилучшими по правилу 1 сравнения векторов по предпочтению оказались вторая и последняя векторные оценки исходного списка V, и соответствующие им варианты решений {b, е) следует также признать наилучшими с учетом оценок, полученных ими по критериями, Y, Z,U.
Заметим, что полученное с использованием правила 1 множество Мп = {b, е) наилучших и несравнимых вариантов решений называют в теории принятия решений областью компромиссов, ют множеством парето-оптималъныхрешений.
Упражнения
1. Определить проекции v : пр , v, пр 3 v, пр j 3 v, если:
a) v = (2, 3,1,1); б) v = (2, 2, 3, 1).
2. Определить проекции множества векторов V: пр1V, пр3 V, пр1.3 V, если:
а) {(2, X 1,1), (2, 2, 3,1), (1,2, 3,1)};
б) {(1,3, 5), (2,4, 6), (3,5, 7)}.
З.ПустьХ= {а, с}, Y= {а, d,f/}. Найти X*Y, Y2, Y*X*Y.
4. Проиллюстрировать на конкретном примере справедливость соотношения
А* (В 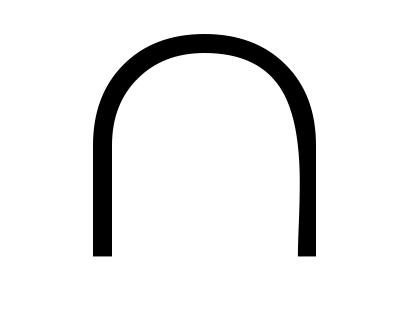 С) С)
(А * В) 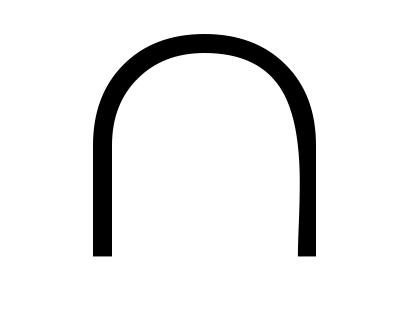 (А * С). (А * С).
5.Пусть А1=А2 = {а, b, с}, А3 = А4= {d, e} и V=A1 * A2*A3*A4. Найти: пр1 V, пр1.3 V.
6. Сравнить векторные оценки множества V= {(3,1,2,3), (2, 2, 1, 3), (1, 2, 3, 2), (3, 1, 2, 2), (1, 2, 2, 3), (3, 2, 3, 2), (2, 2, 2, 2), (2, 3, 1,3)} с использованием правила 1 сравнения векторов по предпочтению и определить подмножество V' наилучших - парето-оптимальных - векторных оценок, V’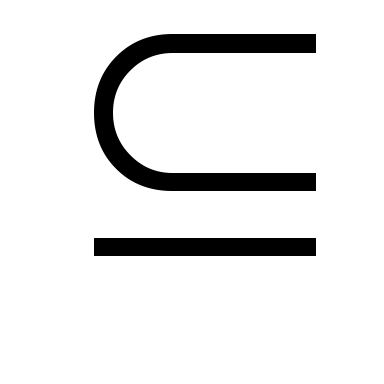 V. V. |
 Скачать 0.61 Mb.
Скачать 0.61 Mb.