статистика. про тьюкиMU_4_5(DA). Дисперсионный анализ
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
3. Апостериорные множественные сравнения среднихРезультат дисперсионного анализа, указывающий, что средние значения отклика для разных уровней фактора, различаются, не является окончательным результатом анализа изучаемого явления. Это скорее промежуточный результат, который подразумевает дальнейшее раскрытие того, для каких уровней фактора средние больше, для каких меньше, а для каких одинаковы. Основная процедура дисперсионного анализа не дает возможности ответить на эти вопросы. Самый очевидный и простой вариант решения данной задачи - провести серию по парных сравнений при помощи t-критерия, используя в качестве оценки дисперсии величину 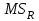 - оценку внутригрупповой дисперсии, полученную в ходе дисперсионного анализа. Такой подход реализуется в так называемом методе наименьшей значимой разности (LSD). Статистика критерия LSD для проверки гипотезы равенства средних - оценку внутригрупповой дисперсии, полученную в ходе дисперсионного анализа. Такой подход реализуется в так называемом методе наименьшей значимой разности (LSD). Статистика критерия LSD для проверки гипотезы равенства средних 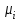 и и 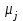 имеет вид: имеет вид: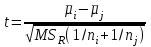 . .Если наблюдаемое значение статистики 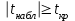 , где , где 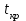 - критическая точка распределения Стьюдента уровня - критическая точка распределения Стьюдента уровня 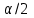 (или квантиль уровня (или квантиль уровня 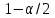 ) с числом степеней свободы ) с числом степеней свободы 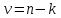 , то нулевая гипотеза отклоняется и принимается гипотеза , то нулевая гипотеза отклоняется и принимается гипотеза 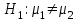 . .Однако, такой подход является не совсем корректным. Если задать, скажем, 5% уровень значимости, то при каждом сравнении вероятность отклонить нулевую гипотезу будет равна 5%, а при серии по парных сравнений вероятность отклонить хотя бы одну нулевую гипотезу в таком случае существенно превысит 5%. Например, при по парном сравнении средних 4 групп, эта вероятность составит 26,5 %. Существуют разные подходы к решению данной проблемы. Один из них – уменьшить уровень значимости при по парном сравнении так, чтобы вероятность хотя бы одного отклонения нулевой гипотезы равнялось заданному уровню значимости. Такой подход реализуется в методе Бонферрони (правильнее говорить о принципе Бонферрони) множественных сравнений, в котором при каждом по парном сравнении задается уровень значимости 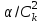 , где , где 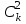 - число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из - число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из 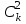 сравнений не превзойдет сравнений не превзойдет 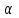 . Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия. . Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия.LSD – критерий и критерий Бонферрони занимают как бы самые крайние позиции в ряду критериев множественных сравнений. Среди остальных критериев множественного сравнения средних можно выделить критерии множественных сравнений Шеффе, Ньюмена-Келса, Тьюки и другие. В методе множественных сравнений Шеффе для проверки гипотезы равенства средних 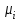 и и 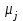 используется статистика: используется статистика: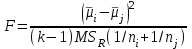 , ,где 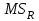 – оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики – оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики 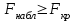 , где , где 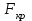 - критическая точка распределения Фишера уровня - критическая точка распределения Фишера уровня 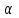 (или квантиль уровня (или квантиль уровня 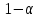 ) с числом степеней свободы ) с числом степеней свободы 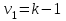 и и 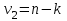 , то нулевая гипотеза отклоняется и принимается гипотеза , то нулевая гипотеза отклоняется и принимается гипотеза 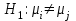 . . Заметим, что в отличии от LSD критерия, где статистика 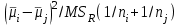 имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет 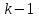 степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана. степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана.В методе множественных сравнений Тьюки (или достоверно значимой разности – HSD) для проверки гипотезы 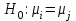 против альтернативы против альтернативы 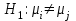 используется статистика: используется статистика: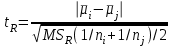 , ,значения которой сравниваются с критическими точками уровня 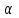 распределения стьюдентизированного размаха с распределения стьюдентизированного размаха с 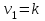 и и 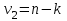 степенями свободы. Если наблюдаемое значение статистики степенями свободы. Если наблюдаемое значение статистики 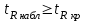 , где , где 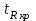 - критическая точка распределения стьюдентизированного размаха уровня - критическая точка распределения стьюдентизированного размаха уровня 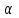 (или квантиль уровня (или квантиль уровня 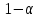 ) с числом степеней свободы ) с числом степеней свободы 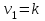 и и 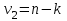 , то нулевая гипотеза отклоняется и принимается гипотеза , то нулевая гипотеза отклоняется и принимается гипотеза 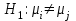 . . Если объемы выборок различаются сильно, то рекомендуется использовать HSD критерий Тьюки для неравных выборок (критерий Spjovoll-Stoline). Статистика критерия в этом случае имеет вид: 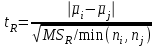 . .Критические точки определяются также, как и для критерия HSD Тьюки. В критерии Ньюмана-Келса используется та же статистика, что и в критерии Тьюки, однако по другому определяются критические точки. В качестве критических точек критерия Ньюмана-Келса используются критические точки распределения стьюдентизированного размаха с 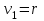 и и 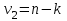 степенями свободы, где степенями свободы, где 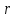 - число средних расположенных между - число средних расположенных между 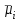 и и 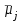 в вариационном ряду выборочных средних, включая в вариационном ряду выборочных средних, включая 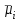 и и 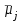 . Например, если сравниваются значения . Например, если сравниваются значения 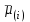 и и 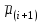 вариационного (упорядоченного) ряда средних, то вариационного (упорядоченного) ряда средних, то 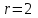 , если сравниваются значения , если сравниваются значения 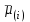 и и 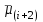 , то , то 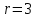 и так далее. и так далее.В пакете STATISTICA используется модифицированный вариант критерия Ньюмана-Келса, в котором в качестве статистики критерия используется величина 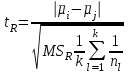 . .Аналогичная статистика используется и в критерии Дункана, но в качестве критических точек берутся точки D-распределения Дункана c 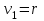 и и 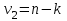 степенями свободы, где степенями свободы, где 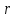 - число средних расположенных между - число средних расположенных между 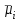 и и 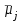 в вариационном ряду выборочных средних, включая в вариационном ряду выборочных средних, включая 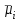 и и 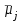 . .Методы множественного сравнения средних можно использовать не только для проверки гипотез о попарном различии средних, а также для проверки гипотез о различии средних для любых выбранных наборов групп. В силу этого, основная гипотеза в данных методах в общем случае имеет вид: 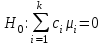 , ,где 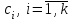 некоторые заданные константы, удовлетворяющие условию некоторые заданные константы, удовлетворяющие условию 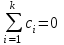 . .Например, при 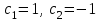 , , 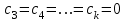 , ,мы будем проверять гипотезу 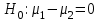 или или 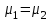 . .При 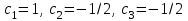 , , 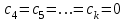 , ,будем проверять гипотезу 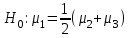 , то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д. , то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д.Линейные комбинации вида: 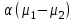 , , 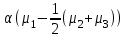 , то есть величины, пропорциональные разности между средними от средних, называются контрастами. , то есть величины, пропорциональные разности между средними от средних, называются контрастами.Критерии LSD, Шеффе, HSD Тьюки легко модифицировать под проверку гипотезы 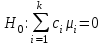 . Например, статистика LSD критерия для проверки гипотезы . Например, статистика LSD критерия для проверки гипотезы 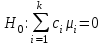 будет иметь вид: будет иметь вид: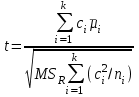 . .Критическими точками статистики, по прежнему, будут являться квантили распределения Стьюдента уровня 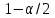 с числом степеней свободы с числом степеней свободы 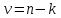 . . |
