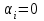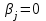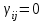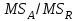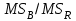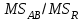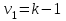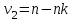статистика. про тьюкиMU_4_5(DA). Дисперсионный анализ
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
2. Многофакторный дисперсионный анализЕсли анализируется одновременное влияние двух и более различных факторов на результаты наблюдений, то используется многофакторный дисперсионный анализ. Например, двухфакторная модель нам потребуется, если мы будем строить модель объяснения различий в средних доходов респондентов не только с учетом места проживания респондента, но и с учетом пола респондента. Пусть мы исследуем влияние на величину 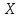 двух факторов A и B, имеющих, соответственно двух факторов A и B, имеющих, соответственно 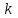 и и 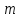 уровней. В двухфакторной модели дисперсионного анализа обычно исходят из следующей модели порождения данных: уровней. В двухфакторной модели дисперсионного анализа обычно исходят из следующей модели порождения данных: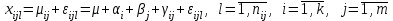 , ,где: 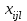 - l-ое наблюдаемое значение отклика для i-го уровня фактора A и j-го уровня фактора B; - l-ое наблюдаемое значение отклика для i-го уровня фактора A и j-го уровня фактора B;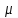 - среднее значение отклика по всей совокупности (генеральное среднее); - среднее значение отклика по всей совокупности (генеральное среднее);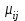 - среднее значение отклика для i-го уровня фактора A и j-го уровня фактора B; - среднее значение отклика для i-го уровня фактора A и j-го уровня фактора B;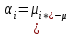 - главный эффект i-го уровня фактора A ( - главный эффект i-го уровня фактора A (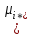 - среднее значение отклика для i-го уровня фактора A); - среднее значение отклика для i-го уровня фактора A);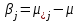 - главный эффект j-го уровня фактора B ( - главный эффект j-го уровня фактора B (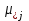 - среднее значение отклика для j-го уровня фактора B); - среднее значение отклика для j-го уровня фактора B);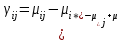 - эффект взаимодействия i-го уровня фактора A и j-го уровня фактора B; - эффект взаимодействия i-го уровня фактора A и j-го уровня фактора B;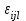 - независимые случайные величины с математическим ожиданием равным нулю и одинаковой дисперсией - независимые случайные величины с математическим ожиданием равным нулю и одинаковой дисперсией 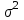 . .Заметим, что эффекты 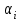 , , 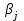 , , 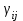 удовлетворяют условиям: удовлетворяют условиям: 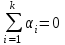 , , 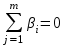 , , 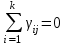 , , 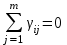 . . Выражение 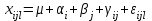 можно представить в виде: можно представить в виде: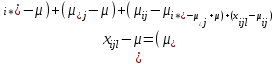 . .Данное соотношение говорит о том, что отклонение наблюдаемого значения отклика складывается из суммы четырех слагаемых: отклонения отклика от среднего значения для i, j-го набора уровней факторов A и B 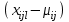 , главных эффектов i-го уровня фактора A и j-го уровня фактора B и эффекта взаимодействия. Что, означает, с учетом указанных выше условий на эффекты, что дисперсия отклика может быть представлена в виде суммы четырех дисперсий, одна из которых характеризует внутригрупповую изменчивость для i, j-го набора уровней факторов A и B, а остальные соответствующие эффекты. , главных эффектов i-го уровня фактора A и j-го уровня фактора B и эффекта взаимодействия. Что, означает, с учетом указанных выше условий на эффекты, что дисперсия отклика может быть представлена в виде суммы четырех дисперсий, одна из которых характеризует внутригрупповую изменчивость для i, j-го набора уровней факторов A и B, а остальные соответствующие эффекты.Разложение общей дисперсии на составляющие для выборочных данных обычно записывается в виде равенства сумм квадратов соответствующих отклонений (которое, вообще говоря, справедливо только в случае выполнения условия пропорциональности 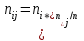 ): ):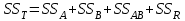 , ,где: 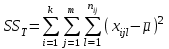 – общая, или полная, сумма квадратов отклонений; – общая, или полная, сумма квадратов отклонений;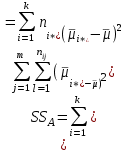 – сумма квадратов отклонений средних по уровням фактора A от общей средней, или сумма квадратов главных эффектов A; – сумма квадратов отклонений средних по уровням фактора A от общей средней, или сумма квадратов главных эффектов A;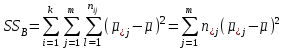 – сумма квадратов отклонений средних по уровням фактора B от общей средней, или сумма квадратов главных эффектов B; – сумма квадратов отклонений средних по уровням фактора B от общей средней, или сумма квадратов главных эффектов B;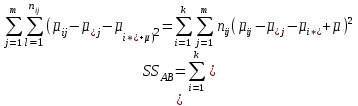 – сумма квадратов взаимодействия эффектов A и B; – сумма квадратов взаимодействия эффектов A и B;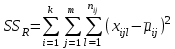 – остаточная сумма квадратов отклонений. – остаточная сумма квадратов отклонений.Число степеней свободы сумм квадратов 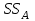 и и 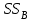 равно соответственно равно соответственно 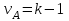 и и 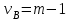 . .Число степеней свободы сумм квадратов взаимодействия эффектов 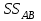 равно равно 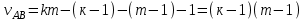 . .Число степеней свободы сумм квадратов остатков 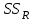 равно равно 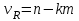 . .Соответственно средние суммы квадратов будут равны: 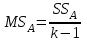 , , 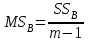 , , 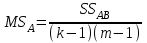 , , 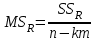 . .Поскольку двухфакторная модель учитывает различные эффекты влияния факторов, то и статистический анализ для двухфакторной модели предполагает проверку гипотез о значимости различных эффектов. В качестве статистик критериев проверки гипотез о значимости соответствующих эффектов используются отношения средней суммы квадратов эффектов к средней сумме квадратов остатков. При условии истинности 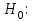 «эффект незначим» и нормальном распределении остатков данные статистики имеют распределение Фишера с параметрами степеней свободы, определяемыми числами степеней свободы соответствующих сумм, участвующих в отношении. В табл. 1 приведены основные рассматриваемые гипотезы, статистики критериев для проверки данных гипотез и соответствующие числа степеней свободы данных статистик. «эффект незначим» и нормальном распределении остатков данные статистики имеют распределение Фишера с параметрами степеней свободы, определяемыми числами степеней свободы соответствующих сумм, участвующих в отношении. В табл. 1 приведены основные рассматриваемые гипотезы, статистики критериев для проверки данных гипотез и соответствующие числа степеней свободы данных статистик. Табл. 1. Статистики для проверки гипотез двухфакторного дисперсионного анализа
Если наблюдаемое значение статистики 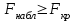 , где , где 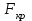 - критическая точка распределения Фишера уровня - критическая точка распределения Фишера уровня 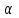 (или квантиль уровня (или квантиль уровня 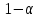 ) с числом степеней свободы ) с числом степеней свободы 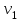 и и 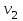 , то нулевая гипотеза отклоняется и считается, что средние для различных уровней фактора значимо различаются. , то нулевая гипотеза отклоняется и считается, что средние для различных уровней фактора значимо различаются. |