статистика. про тьюкиMU_4_5(DA). Дисперсионный анализ

• Название: Дисперсионный анализ
• Анкор: статистика
• Дата: 20.01.2023
• Размер: 1.5 Mb.
• Имя файла: про тьюкиMU_4_5(DA).docx
• Тип: Документы; #896353
• страница: 5 из 5

Пример 2. Результаты ответов 400 респондентов на вопросы анкеты «Томск 400» «Как Вы оцениваете Ваше здоровье в сравнении со здоровьем Ваших сверстников» (варианты ответов: “Очень хорошее”, “Хорошее”, “Среднее”, “Плохое”, “Очень плохое”, “Затрудняюсь ответить”) представлены в виде числовой выборки кодов ответов со значениями, соответственно, {1,2,3,4,5,6}. Также имеется выборка числовых кодов, соответствующих месту проживания респондента (1 – «Томск», 2 - «Северск», 3 – «Томский район», 4 - «Асино», 5 – «Асиновский район», 6 - «Каргасокский район», 7 – «Каргасок», 8 - «Тегульдет»). Используя дисперсионный анализ, установить, одинаково ли оценивают свое здоровье респонденты в различных населенных пунктах.

Поскольку зависимая переменная (варианты ответов на вопрос «Как Вы оцениваете Ваше здоровье в сравнении со здоровьем Ваших сверстников») категориального типа, то для выявления различия в ответах на вопросы респондентов различных населенных пунктов используем непараметрический дисперсионный анализ Краскела-Уоллиса.

Выборочные данные представлены в нашей таблице данных под именами «В_13» и «НП». Чтобы исключить из рассмотрения респондентов, давших на вопрос «Как Вы оцениваете Ваше здоровье в сравнении со здоровьем Ваших сверстников» ответ «Затрудняюсь ответить», незабываем указать код категории, которые мы исключаем из анализа. Для этого в таблице данных кликаем дважды на имени переменной «В_13» и в раскрывшемся окне свойств переменной устанавливаем значение параметра «MD code» равным значению 6 (код ответа «Затрудняюсь ответить»).

Предварительно можно качественно оценить различие средних, построив диаграммы размаха в соответствующем разделе модуля «Descriptive statistics». Однако, это можно будет сделать и непосредственно в модуле непараметрического дисперсионного анализа.

Для проведения непараметрического дисперсионного анализа рангов Краскела-Уоллиса проделаем следующее. Запускаем в головном меню модуль «Statistics», в стартовой панели выбираем пункт «Nonparametrics». В меню модуля «Nonparametric Statistics» (рис. 27) выбираем раздел «Comparing multiple indep. Samples (groups)» («Сравнение нескольких независимых выборок)».



Рис. 27. Выбор метода непараметрического дисперсионного анализа в стартовом окне модуля «Nonparametric Statistics»

В появившемся окне модуля «Kruskal-Wallis ANOVA and Median Test» (рис. 28), выбираем переменные, нажав на кнопку «Variables». В качестве зависимой переменной выбираем переменную «В_13» а в качестве группирующей – переменную «НП».



Рис. 28. Окно модуля непараметрического дисперсионного анализа

Оценим предварительно качественно различие средних по уровням фактора. Для этого нажимаем на кнопку «Box & whisker», в качестве переменной выбираем «В_13», а в качестве параметров для диаграммы типа «ящики-усы» параметры «Median / Quart / Range» («Медиана / Квартильный размах / Полный размах». В результате получаем диаграмму, изображенную на рис. 29. Как видим, на основе данной диаграммы трудно что-либо сказать о различии средних. Количество уровней зависимой переменной невелико, поэтому медианы для всех категорий переменной «НП» совпадают, и, соответственно, все интервалы размаха перекрываются. Но совпадение самих значений медиан, еще не означает, что число значений больших (меньших) медианы для разных уровней фактора одинаково. Парадокс, но мы проверяем гипотезу о “различии” медиан, при условии их “равенства”! Дело в том, что со статистической точки зрения, медиана просто делит всю совокупность в определенном соотношении (причем не обязательно 50% на 50% - смотри внимательно определение медианы). И если эти соотношения для выборок различаются, это и означает различие медиан двух совокупностей.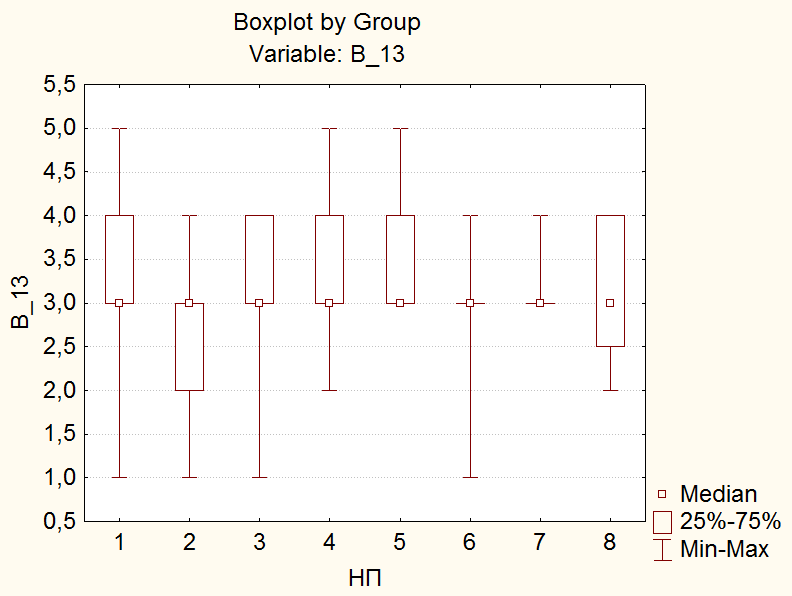



Рис. 29. Диаграммы размаха по категориям переменной «НП»

Вернемся в окно непараметрического дисперсионного анализа (рис. 5.30). Нажав на кнопку «Summary», в рабочей книге в разделе «Kruskal-Wallis ANOVA and median test dialog» на странице «Kruskal-Wallis ANOVA by Ranks» получим результаты дисперсионного анализа Краскела-Уоллиса, а на странице «Median Test» результаты медианного теста.

Согласно результатам дисперсионного анализа Краскела-Уоллиса (рис. 30), существует статистически значимое ( 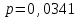) влияние уровней фактора «НП» на значения переменной «В_13». Другими словами, респонденты в различных населенных пунктах по разному оценивают свое здоровье.

Результаты медианного теста также показывают различие в ответах для различных населенных пунктов (рис. 31) на уровне . В медианном тесте выдается также информация о наблюдаемом числе («observed») значений, меньше либо равных медианы (и, соответственно, больше медианы), и о ожидаемом числе («expected») тех же значений, вычисленном при условии истинности нулевой гипотезы о равенстве медиан признака «В_13» при различных уровнях фактора «НП». Ориентируясь на эти значения, можно сделать выводы о том какие группы и как различаются.



Рис. 30. Результаты дисперсионного анализа Краскела-Уоллиса



Рис. 31. Результаты медианного теста

Так, для г. Томска (НП = 1) число наблюдаемых значений больших медианы (57) больше ожидаемого (49,6203). Это предположительно означает, что респонденты г. Томска хуже оценивают свое здоровье, чем, например, респонденты г. Северска (НП = 2), для которых число наблюдаемых значений больших медианы (3) меньше ожидаемого (12,65316).

Статистически определить между какими группами наблюдается значимое различие можно, используя множественное апостериорное сравнение средних рангов. Чтобы получить результаты множественного сравнения рангов в окне модуля «Kruskal-Wallis ANOVA and Median Test» нажимаем кнопку «Multiple сomparisons of mean ranks for all groups», в результате получаем таблицу, изображенную на рис. 32. Как видим, только для пары г. Томск – г. Северск можно считать, что существует слабо значимое различие ( ). Поскольку данный результат был получен после значимого результата дисперсионного анализа, следует признать, что эта пара и определила результат дисперсионного анализа.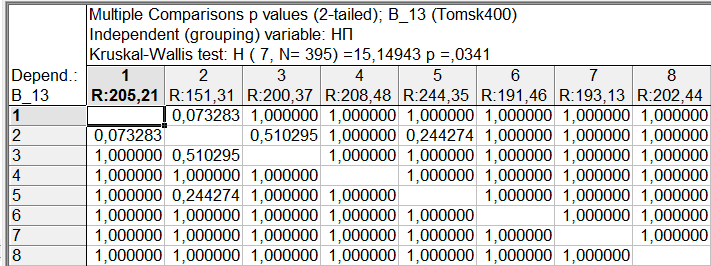



Рис. 32. Результаты множественного сравнения средних рангов

Таким образом, окончательный результат дисперсионного анализа: есть значимое различие в оценке своего здоровья респондентами г. Томска и г. Северска - респонденты г. Томска хуже оценивают свое здоровье, чем респонденты г. Северска. Различие в оценках своего здоровья респондентами других населенных пунктов, как между собой, так и в сравнении с г. Томск и г. Северск статистически незначимо.
Пример 3. Используя двухфакторный дисперсионный анализ, установить значимость совместного влияния таких факторов, как пол и место проживания респондента на уровень заявленных в ходе анкетирования хронических невралгических (в том числе слух, зрение) заболеваний.

В примере 1 был проведен однофакторный дисперсионный анализ, согласно которому была установлено различие заявленного уровня некоторых хронических заболеваний (в том числе невралгических) в различных населенных пунктах. Аналогичный однофакторный анализ можно было бы провести, чтобы выяснить различаются ли уровни заявленных хронических заболеваний в зависимости от пола респондентов.

Можно провести анализ влияния одновременно двух факторов (места проживания и пола) на уровень заболеваний без учета взаимодействия факторов. Такой факторный анализ является частным случаем многофакторного дисперсионного анализа и называется дисперсионным анализом главных эффектов (Main effects ANOVA).

Классический же многомерный анализ в отличии от анализа главных эффектов предполагает, кроме того, анализ эффектов взаимодействия факторов.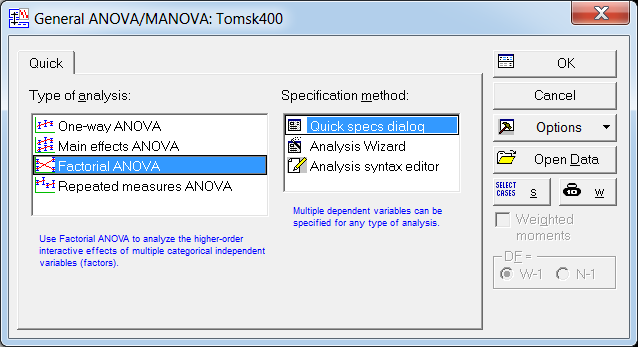



Рис. 33. Выбор метода дисперсионного анализа

Для проведения двухфакторного анализа запускаем в головном меню модуль «Statistics» и в стартовой панели выбираем пункт «ANOVA». В появившемся окне (рис. 33) выбираем тип анализа («Factorial ANOVA» - многофакторный дисперсионный анализ) и задаем метод («Quick specs dialog - диалог быстрых спецификаций»). После нажатия на «OK», попадаем в окно выбора переменных для анализа (рис. 34).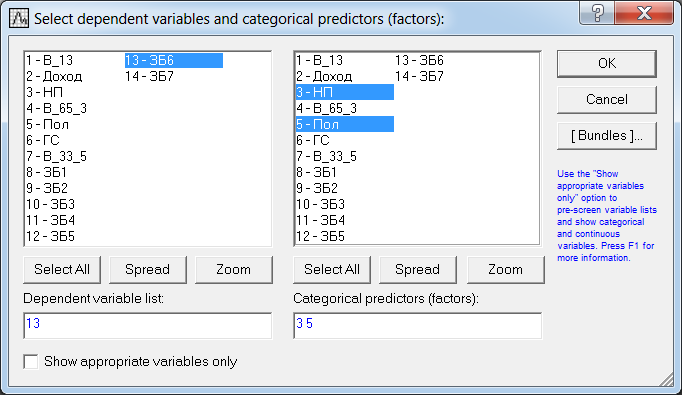



Рис. 34. Выбор переменных для дисперсионного анализа

Выбираем в качестве зависимой переменной переменную «ЗБ6» (которая содержит коды «1» и «0», соответствующие наличию или отсутствию заболевания), а в качестве группирующих переменных (факторов) - переменные «НП» и «Пол». Можно также выбрать уровни (коды) группирующих переменных, по которым будет проводиться анализ. Если коды не задавать, анализ будет проводиться по всем уровням группирующих переменных. После нажатия на клавишу «OK» переходим в окно результатов дисперсионного анализа – «ANOVA Results 1» и выбираем вкладку «Summary» (рис. 15).

Для просмотра описательной статистики на вкладке «Summary» следует выбрать «Cell statistics». Для просмотра результатов дисперсионного анализа выбираем «Univariate results», в результате получаем таблицу, изображенную на рис. 35.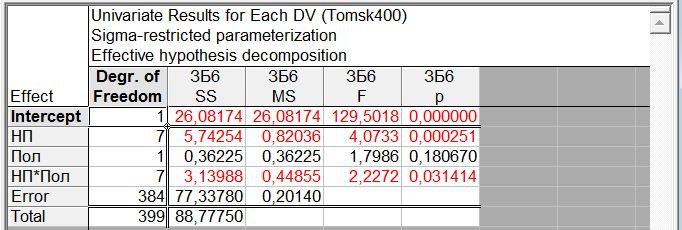



Рис. 35. Результаты многофакторного дисперсионного анализа

Первую строку таблицы (эффект «Intercept») можно проигнорировать. Во второй и третьих строках таблицы приводятся эффекты факторов «НП» и «Пол» - суммы квадратов отклонений (SS), средние суммы квадратов отклонений (MS) с указанием значения статистики Фишера 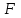и наблюдаемого уровня значимости. 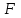В четвертой строке таблицы приводится эффект взаимодействия факторов «НП» и «Пол», также с указанием значения статистики Фишера и наблюдаемого уровня значимости. В пятой строке таблицы приводятся суммы квадратов отклонений (SS), средние суммы квадратов отклонений (MS) для остатков или внутригруппового разброса. В последней строке указана полная сумма квадратов отклонений.

Как видим из таблицы результатов дисперсионного анализа, значимыми эффектами является эффект фактора «НП» и эффект взаимодействия факторов «НП» и «Пол», при этом эффект фактора «Пол» не является значимым.

Для построения графиков средних разных эффектов на вкладке «Summary» нажимаем на кнопку «All effects/Graphs» и в появившемся окне выбираем эффект, для которого будут построены графики средних с доверительными интервалами. На рис. 36 приведен график средних для эффекта «НП», а на рис. 37 графики средних для эффекта взаимодействия факторов «НП» и «Пол».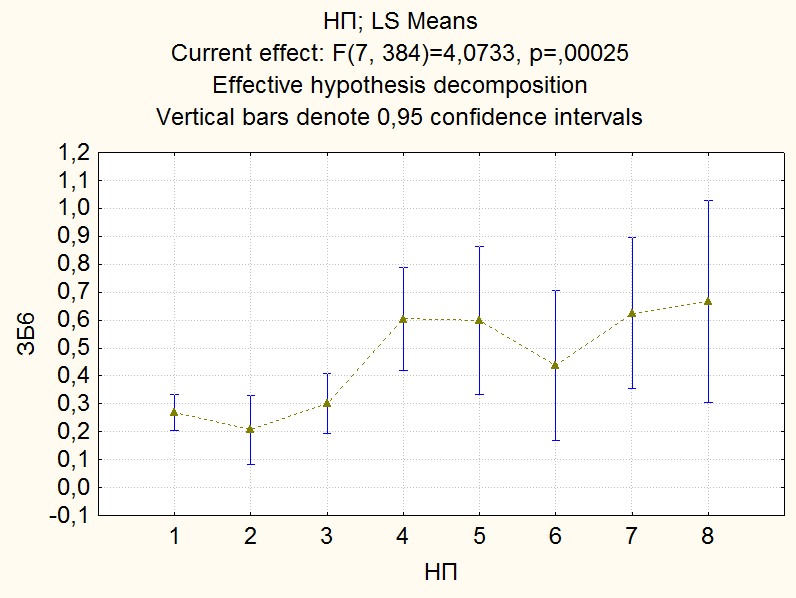



Рис. 36. График средних для эффекта «НП»

Сравнивая графики, можно сделать вывод, что наблюдаемое различие уровня заболеваний для населенных пунктов 1 и 4, 2 и 4, 3 и 4 обусловлено в первую очередь, различием уровня заболеваний для женщин данных населенных пунктов. Для мужчин же, судя по графикам, уровень заболеваний для данных населенных пунктов вряд ли значимо различается.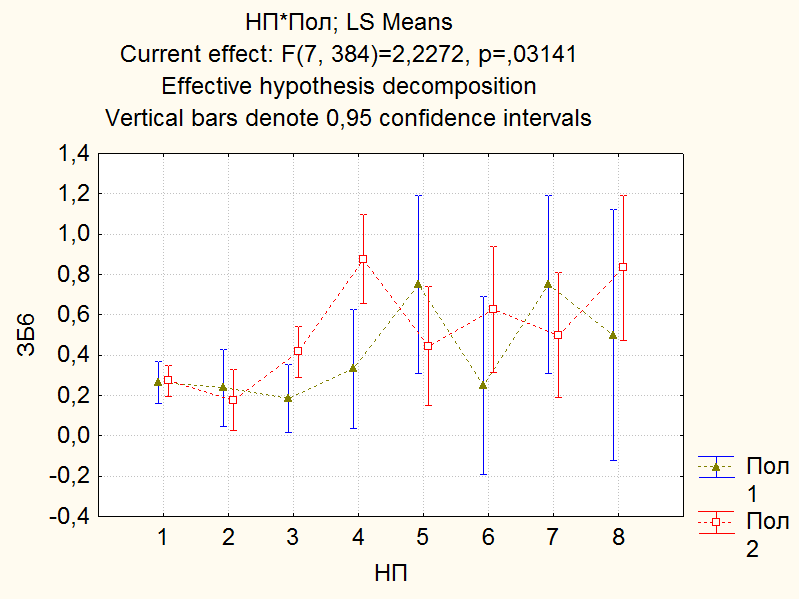



Рис. 37. Графики средних для эффектов «НП*Пол»

Для выявления значимо различающихся средних эффекта взаимодействия используем метод множественных сравнений.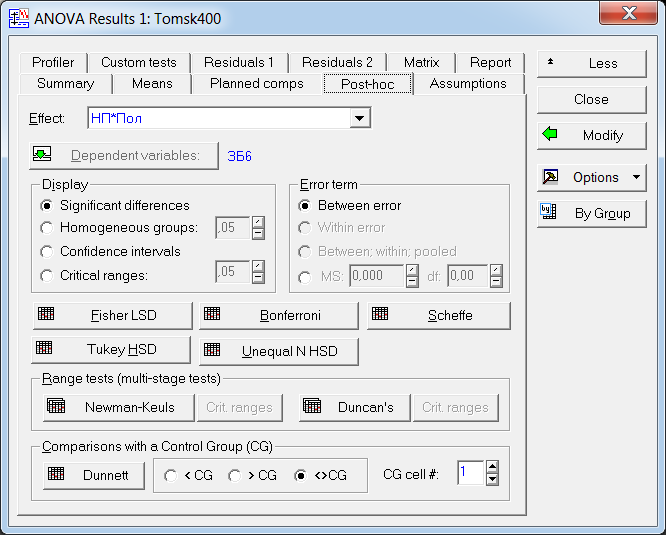



Рис. 38. Выбор метода множественных сравнений для эффекта взаимодействия «НП*Пол»

Для этого в модуле результатов дисперсионного анализа – «ANOVA Results 1», путем нажатия кнопки «More results», выбираем расширенный режим, переходим на вкладку апостериорных сравнений средних «Post-hoc», выбираем эффект «НП*Пол» и выбираем один из методов множественного сравнения, например, средний по консервативности метод HSD Тьюки (рис. 38). Для режима отображения (параметр «Display») устанавливаем «Significant differences» (значимые разности).В результате получим таблицу уровней значимости попарных различий средних для всех комбинаций уровней факторов «НП» и «Пол», часть которой приведена на рис. 39.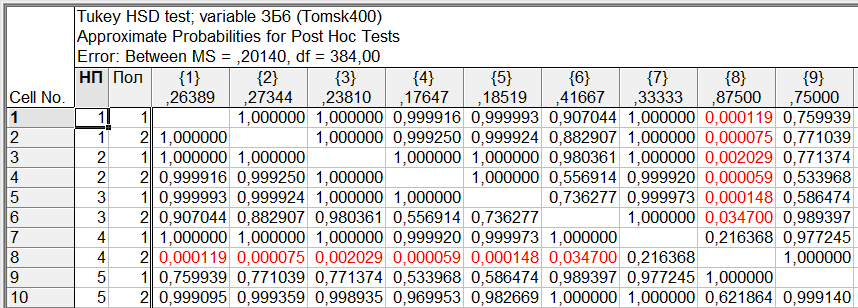



Рис. 39. Уровни значимости для попарных различий средних для всех комбинаций уровней факторов «НП» и «Пол»

Из таблицы видно, что значимое различие средних (заявленных частот заболеваний) существует между женщинами, проживающими в г. Асино и респондентами обеих полов, проживающих в г. Северске, в г. Томске и Томском районе.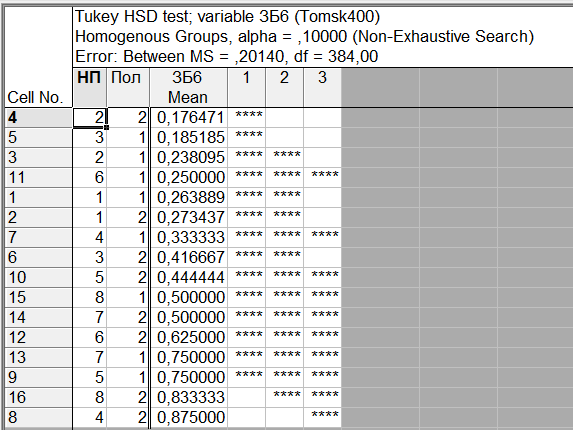



Рис. 40. Однородные кластеры групп в соответствии с выбранным критерием множественного сравнения (HSD Тьюки) и заданным уровнем значимости

Можно также, как это было сделано в примере 1, выделить однородные группы статистически не различающиеся по уровню заболеваний. На вкладке «Post-hoc» для режима отображения (параметр «Display») устанавливаем значение «Homogeneous groups» (однородные группы). Задаем уровень значимости, например, 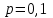(чем больше уровень, тем более близкие группы будут выделены) и выбираем вновь критерий множественного сравнения HSD Тьюки. В результате получаем однородные кластеры групп, расположенные в порядке возрастания средних значений (рис. 40).

Как видим для данного значения уровня значимости, на основе критерия Тьюки, можно выделить три однородные группы, содержащие сочетания факторов в соответствии с таблицей на рис. 39. Заметим, что для некоторых населенных пунктов мужчины и женщины могут быть отнесены к разным группам однородности.