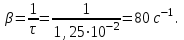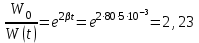Вариант 6
1. Шар массой 1 кг, движущийся горизонтально со скоростью v1, столкнулся с неподвижным шаром большей массы и потерял при этом 80% своей кинетической энергии. Какова масса второго шара? Удар прямой, абсолютно упругий, центральный. Ответ: 𝑚2=2.62 кг
m1 = 1 кг
∆Т1 = 60 %
|
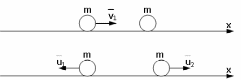
Для абсолютно упругого удара выполняются законы сохранения импульса:
p1 = p2; m1v1 = –m1u1 + m2u2
и энергии
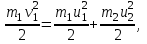
где v1 – скорость шара массой m1 до столкновения, u1 и u2 – cкорости шаров
после столкновения. Закон сохранения импульса записан в предположении, что после столкновения шар массой m1 покатился в обратном направлении.
По условию ∆Т1 = 36%, т.е.
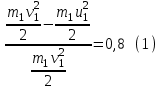
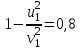
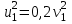
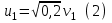
Из закона сохранения энергии получим:
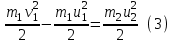
Из уравнения (1) получим:
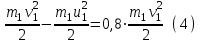
Поскольку левые части уравнений (3) и (4) равны , то можно приравнять и правые:
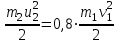
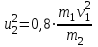
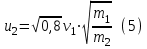
Подставим выражения для скоростей u1 и u2 из (2) и (5) в закон сохранения импульса :
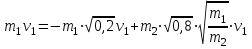
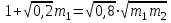
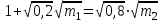
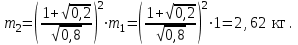
|
m2 ― ?
|
Ответ: m2 = 2,62 кг .
2. Спираль в чайнике состоит из двух одинаковых секций. Сопротивление каждой секции 25 Ом. Через сколько времени закипит 2,5 литра воды, если: 1) включена одна секция; 2) обе секции включены последовательно; 3) обе секции включены параллельно. Начальная температура воды 200 С, напряжение в сети 220 В, КПД нагревателя 80%. Изобразить электрическую схему подключения для данной задачи. Ответ: 𝑡1=541 с; 𝑡2=1082 с;𝑡3=271 с
R = 25 Ом
V = 2,5*10-3 м3
Т0 = 293 К
u = 220 В
η = 0,8
|
Решение.
1) включена одна секция
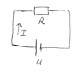
Покажем рисунок. Согласно закону Джоуля-Ленца на секции с сопротивлением R выделяется количество теплоты:
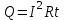 , где I – сила тока, R – сопротивление, t – время. , где I – сила тока, R – сопротивление, t – время.
Согласно закону Ома:
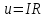 (u - напряжение) (u - напряжение)
Тогда исключая ток I имеем:
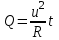
Количество теплоты, переданное воде, с учётом КПД есть:
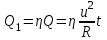
Далее, при нагреве воды до закипания Т2 = 373 К требуется количество теплоты
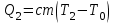 , где , где 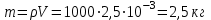 - масса воды, с – её теплоёмкость. - масса воды, с – её теплоёмкость.
В силу закона сохранения энергии
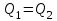
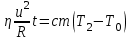
Откуда:
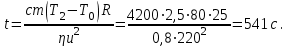
2) Обе секции включены последовательно
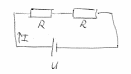
Покажем рисунок. Эквивалентное сопротивление при последовательном соединении
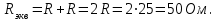
Тогда, как следует из пункта (1)
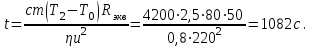
3) обе секции включены параллельно
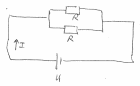
Покажем рисунок. Эквивалентное сопротивление при параллельном соединении:
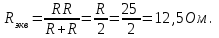
Тогда:
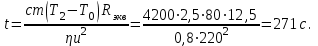
|
t ― ?
|
Ответ: 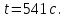 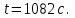 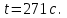
3. За время релаксации в колебательном контуре совершается 12,5 колебаний. Частота колебаний контура 1 кГц. Определить коэффициент затухания. Во сколько раз изменится энергия контура за время равное 5 мс. Изобразить график затухающих колебания для энергии, соответствующих уравнению 𝑊(𝑡) в пределах двух времён релаксации. Примечание: изобразите на рисунке электрический колебательный контур, в котором возникают свободные затухающие колебания. Ответ: 𝛽=80 с−1;𝑊0/𝑊𝑡=2.23;
N = 12,5
ν = 1000 Гц
t = 5*10-3 c
|
Решение.
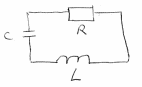
Покажем рисунок. На рисунке показан колебательный контур (R – сопротивление, L – индуктивность, С - ёмкость), в котором происходят затухающие колебания.
При затухающих колебаниях амплитуда колебаний тока меняется по закону:
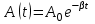 , а энергия колебаний, пропорциональная А2 меняется по закону: , а энергия колебаний, пропорциональная А2 меняется по закону:
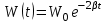 (A0 и W0 – начальная амплитуда и энергия колебаний), где β – коэффициент затухания. Причём: (A0 и W0 – начальная амплитуда и энергия колебаний), где β – коэффициент затухания. Причём:
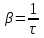 , где τ – время релаксации. , где τ – время релаксации.
По условию этой задачи время релаксации есть:
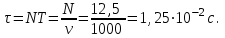 , где , где 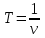 - период колебаний, ν – частота. - период колебаний, ν – частота.
Тогда:
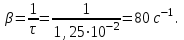
Тогда за время t = 5*10-3 c
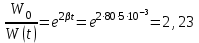
То есть, за это время энергия колебаний уменьшилась в 2,23 раз.
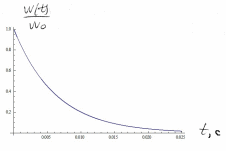
График зависимости энергии колебаний 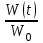 от времени t в пределах от 0 до 2τ показан на рисунке. от времени t в пределах от 0 до 2τ показан на рисунке.
|
β ― ?
W0/Wt ― ?
График ― ?
|
Ответ: 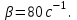 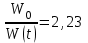 График зависимости энергии колебаний График зависимости энергии колебаний 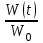 от времени t в пределах от 0 до 2τ показан на рисунке. от времени t в пределах от 0 до 2τ показан на рисунке.
 |
 Скачать 0.52 Mb.
Скачать 0.52 Mb.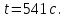
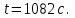
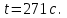
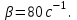
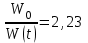 График зависимости энергии колебаний
График зависимости энергии колебаний 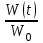 от времени t в пределах от 0 до 2τ показан на рисунке.
от времени t в пределах от 0 до 2τ показан на рисунке.

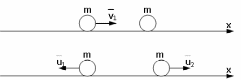
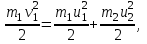
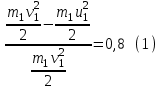
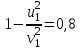
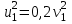
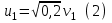
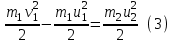
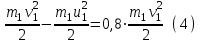
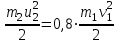
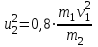
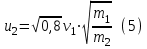
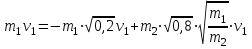
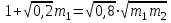
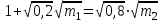
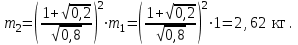

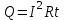 , где I – сила тока, R – сопротивление, t – время.
, где I – сила тока, R – сопротивление, t – время.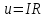 (u - напряжение)
(u - напряжение)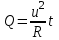
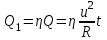
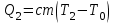 , где
, где 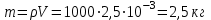 - масса воды, с – её теплоёмкость.
- масса воды, с – её теплоёмкость.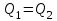
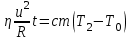
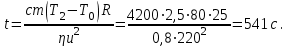

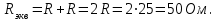
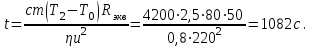

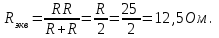
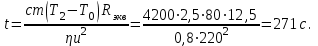

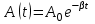 , а энергия колебаний, пропорциональная А2 меняется по закону:
, а энергия колебаний, пропорциональная А2 меняется по закону: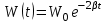 (A0 и W0 – начальная амплитуда и энергия колебаний), где β – коэффициент затухания. Причём:
(A0 и W0 – начальная амплитуда и энергия колебаний), где β – коэффициент затухания. Причём: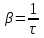 , где τ – время релаксации.
, где τ – время релаксации.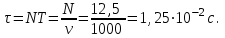 , где
, где 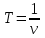 -
-