Математическая статистика. Вариант №8. ВЗФЭИ. 2019.. Для проверки качества поступившей на элеватор партии зерна по схеме собственно случайной бесповторной выборки произведено 10%ное обследование

• Название: Для проверки качества поступившей на элеватор партии зерна по схеме собственно случайной бесповторной выборки произведено 10%ное обследование
• Дата: 22.02.2023
• Размер: 0.58 Mb.
• Имя файла: Математическая статистика. Вариант №8. ВЗФЭИ. 2019..doc
• Тип: Задача; #950201
• страница: 2 из 2

Задача №2
Распределение 50 российских коммерческих банков по объему вложений в ценные бумаги ξ (млн. руб.) и полученной прибыли  (тыс. руб.) представлено в таблице:

\ξ	100-120	120-140	140-160	160-180	180-200	200-220	Итого
1000-1300	4	2	1				7
1300-1600	2	4	2	2			10
1600-1900		4	7	5	1		17
1900-2200			3	4	1	2	10
2200-2500				1	3	2	6
Итого	6	10	13	12	5	4	50

1) вычислить групповые средние и и построить эмпирические линии регрессии;

2) предполагая, что между переменными ξ и  существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

б) вычислить коэффициент корреляции; на уровне значимости  = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными ξ и ;

в) используя соответствующее уравнение регрессии, оценить среднюю прибыль, полученную коммерческим банком, вложившим в ценные бумаги 145 млн. руб.


Решение:
1) Вычислим групповые средние и .

Пусть х = ξ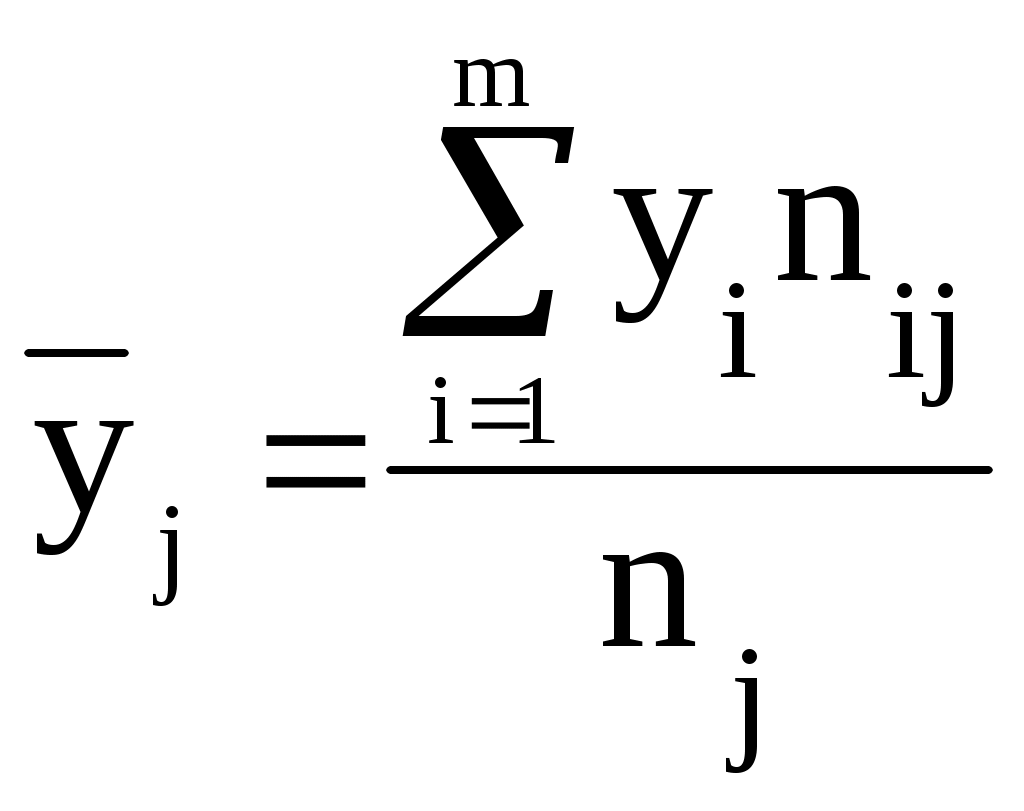, 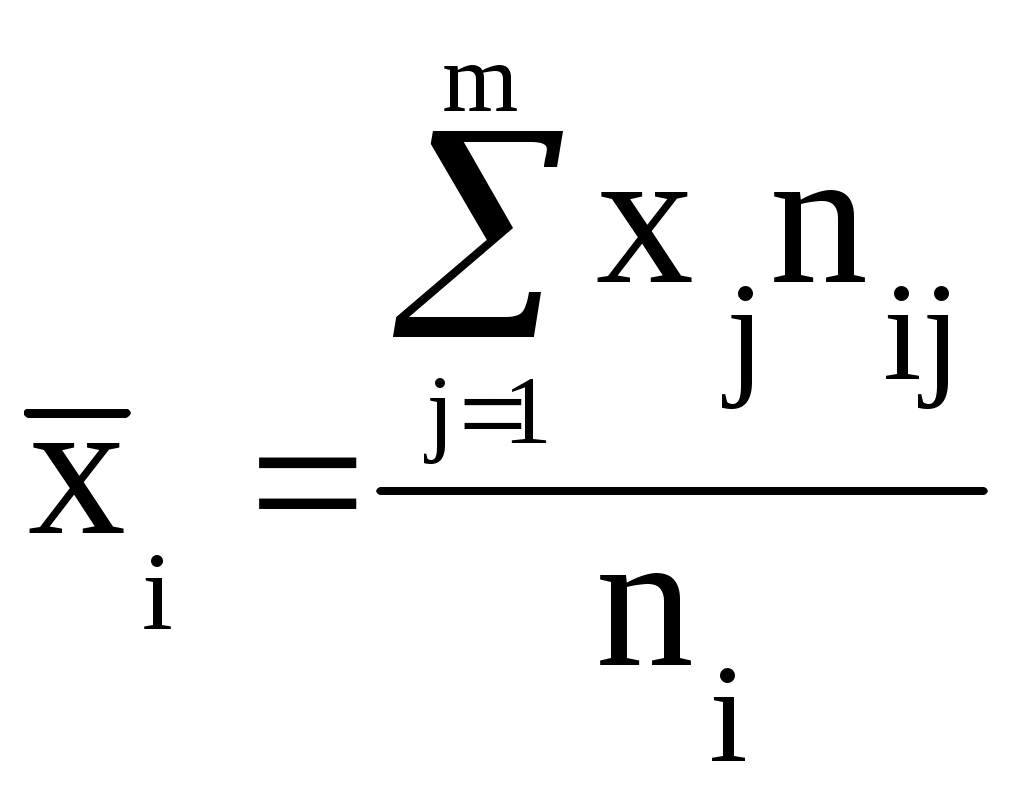у = .

,

1250 тыс. руб.

1510 тыс. руб.

1727 тыс. руб.

1850 тыс. руб.

2170 тыс. руб.

2200 тыс. руб.

х	110	130	150	170	190	210
	1250	1510	1727	1850	2170	2200

Между объемом вложений в ценные бумаги и размером полученной прибыли присутствует прямая связь, т.е. с ростом объема вложений в ценные бумаги по группам увеличивается и размер прибыли в среднем на один коммерческий банк.

121 млн. руб.

138 млн. руб.

154 млн. руб.

174 млн. руб.

193 млн. руб.

у	1150	1450	1750	2050	2350
	121	138	154	174	193

Между размером полученной прибыли и объемом вложений в ценные бумаги присутствует прямая связь, т.е. с ростом размера полученной прибыли по группам увеличивается и объем вложений в ценные бумаги в среднем на один коммерческий банк.

Построим эмпирические линии регрессии (рис. 2.1).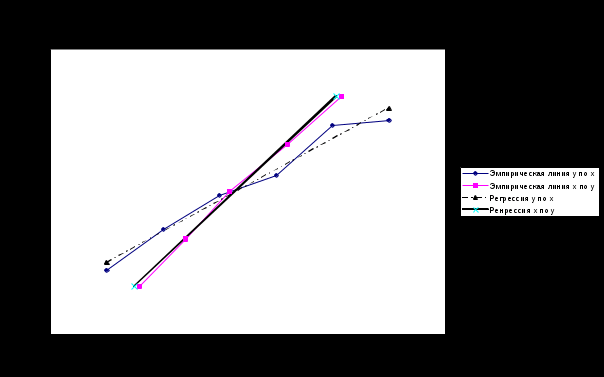



2) a) Определим уравнения прямых регрессии.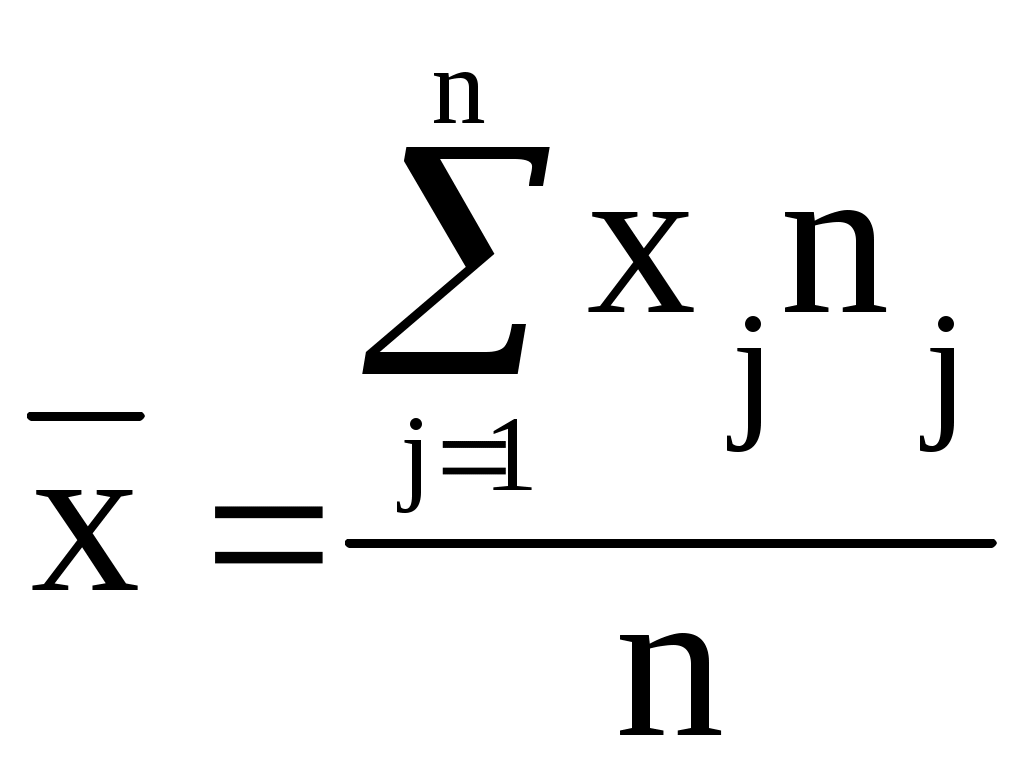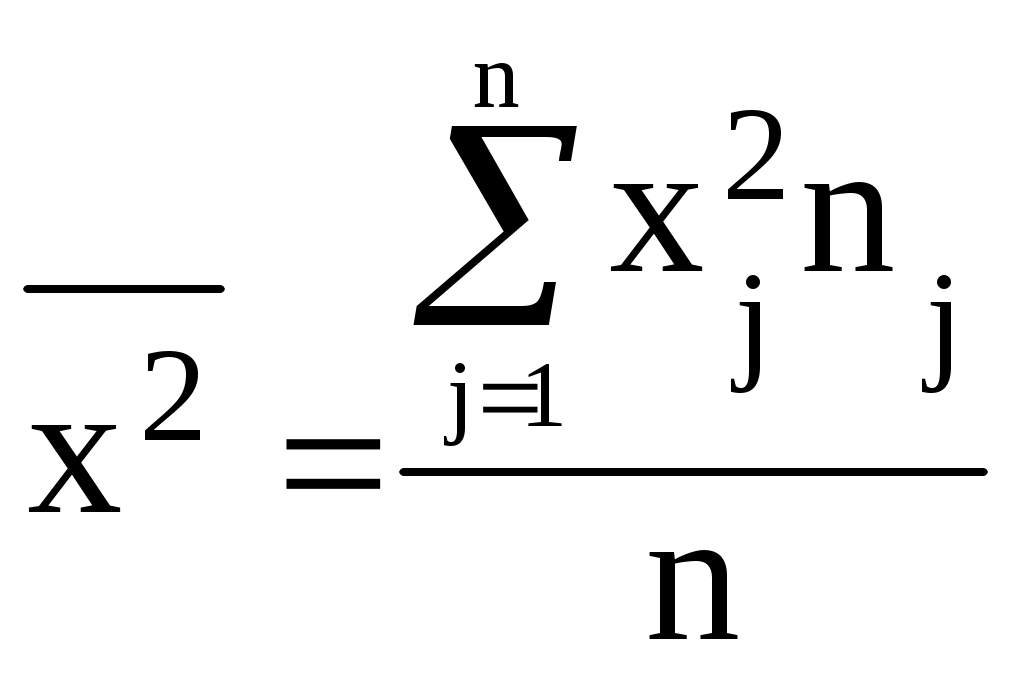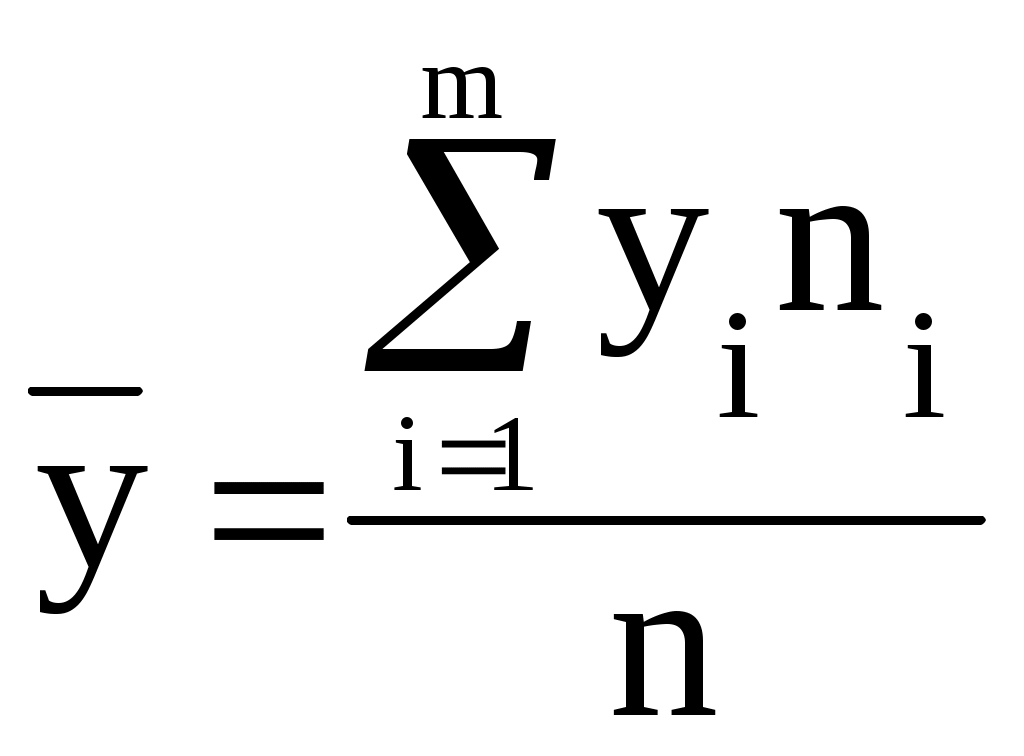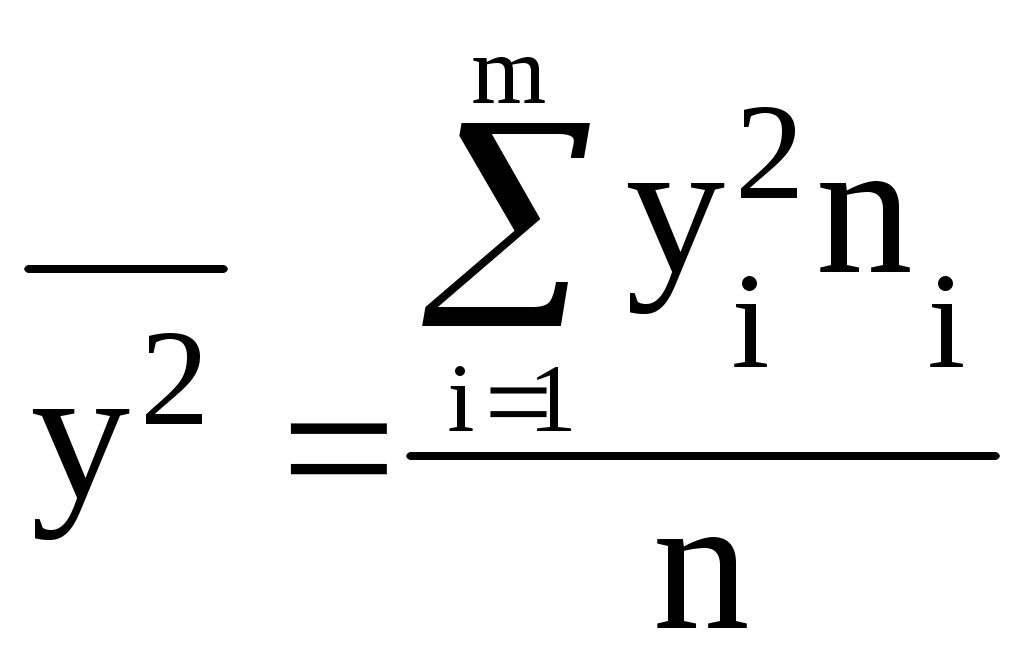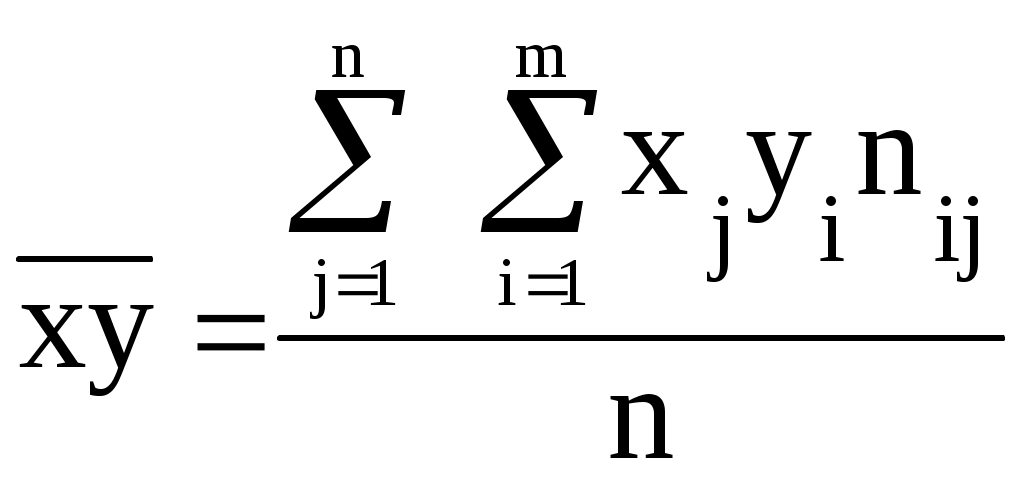









=









=







Уравнение регрессии у по х имеет вид:

у - = ∙(х – ),

где

9,758

у – 1738 = 9,758∙(х – 154,8)

Отсюда:

у = 9,758х + 227,482

х	110	210
у	1301	2277

С увеличением объема вложений в ценные бумаги на 1 млн. руб. размер полученной банком прибыли увеличится на 9,758 тыс. руб.

Уравнение регрессии х по у имеет вид:

х - = ∙(у – ),

где

0,060

х – 154,8 = 0,060∙(у – 1738)

Отсюда:

х = 0,060у + 50,920

у	1150	2350
х	120	191

С увеличением размера полученной прибыли на 1 тыс. руб. объем вложений банком в ценные бумаги увеличится на 0,060 млн. руб.

Построим графики прямых на одном графике с эмпирическими линиями регрессии (рис. 2.1).

б) Определим коэффициент корреляции.





Оценим его значимость с помощью t-критерия Стьюдента.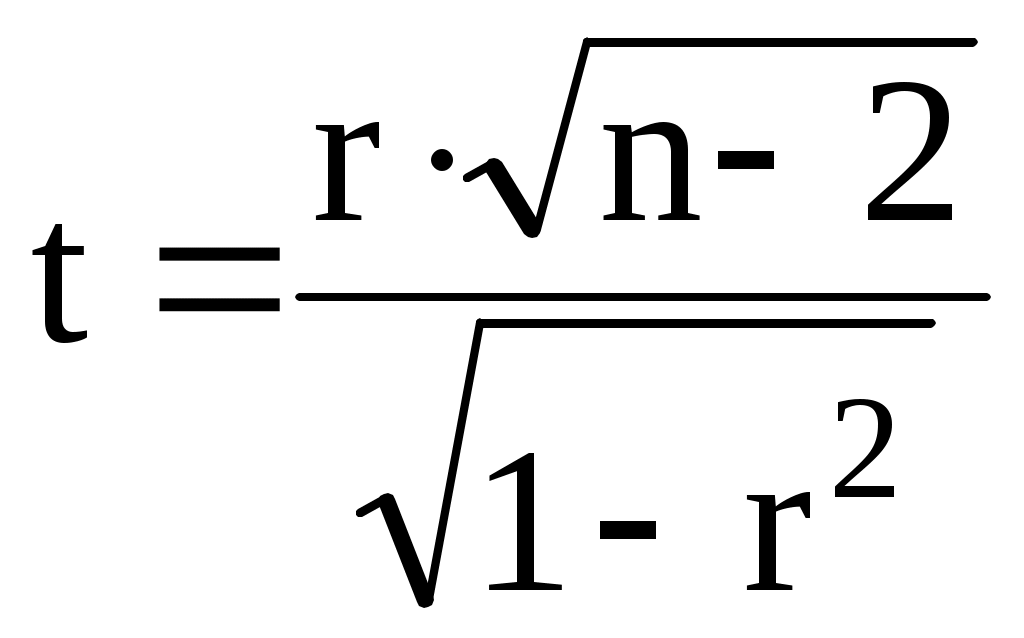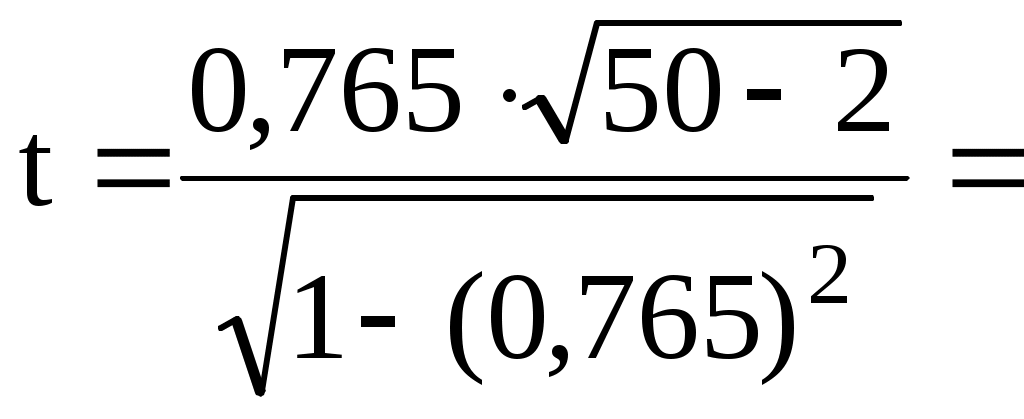



8,23

По таблице критических точек распределения Стьюдента при a = 0,05 и числе степеней свободы k = n – 2 = 50 – 2 = 48 имеем:

2,01

Так как t > , то коэффициент корреляции статистически значим. Связь между изучаемыми признаками прямая и высокая по тесноте связь (по шкале Чеддока).

в) х = 145 млн. руб.

у(145) = 9,758∙145+ 227,482 = 1642 тыс. руб.

Средняя прибыль, полученная коммерческим банком, вложившим в ценные бумаги 145 млн. руб., составит 1642 тыс. руб.

Список литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2006. – 573с.