Для структурной схемы сау, соответствующей выбранному варианту, выполнить следующие действия
 Скачать 452.51 Kb. Скачать 452.51 Kb.
|
|
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Схема: 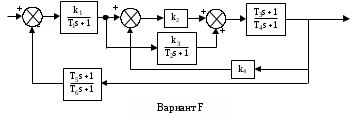 Для структурной схемы САУ, соответствующей выбранному варианту, выполнить следующие действия: Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы. Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики разомкнутой системы. Построить годограф АФЧХ разомкнутой системы. Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы. Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы. Определить устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик. Найти запасы устойчивости системы по фазе и по амплитуде. Найти передаточную функцию замкнутой системы и проверить выводы пункта 6 с помощью частотного критерия Михайлова. Определить величину поправочного коэффициента усиления, при котором статическая ошибка замкнутой системы будет не больше 0.1; перерегулирование в системе составит 12 %; время переходного процесса будет минимальным. Построить с переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование и время регулирования) в системе. ЗАДАНИЕ 1. Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы. 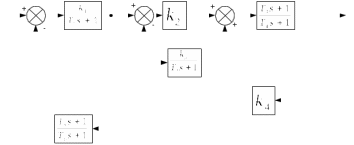 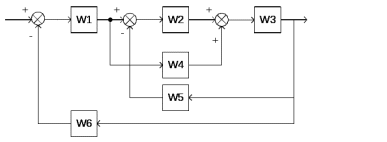 Рис.1. Заданная структурная схема Передаточные функции звеньев: W1 (p) 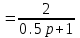 ; W3 (p) ; W3 (p) 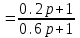 ; W5 (p) =19; ; W5 (p) =19; W2(p)=2; W4 (p) 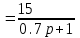 ; W6 (p) ; W6 (p) 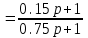 ; ; Избавимся от всех перекрестных параллельных и обратных связей, приведем структурную схему к стандартному виду. Определим передаточную функцию разомкнутой системы, запишем ее в стандартной форме. Определим степень астетизма системы. 1.Перенесем сумматор с выхода на вход звена. 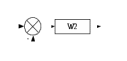  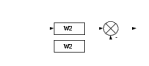 W1 W2 W3          + + +    + - W4  W2 W5   W6  2. Поменяем местами сумматоры. W1 W2 W3          + + +   + -   W4  W2 W5  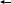 W6  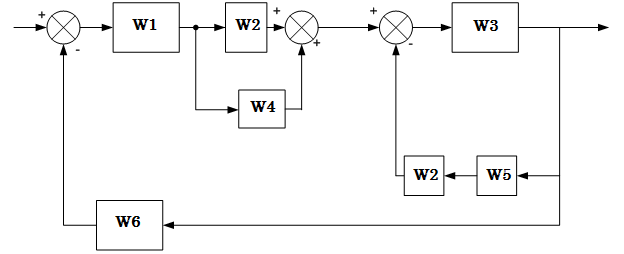 3. Преобразуем систему с сумматором и с единичной обратной связью. W7(р)= W2+W4 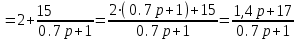 ; ;W8(р) 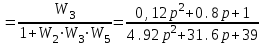 ; ;Заменим последовательно-параллельные соединения звеньев эквивалентным звеном.  Wэкв(р) 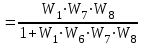 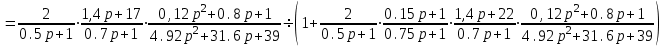 = =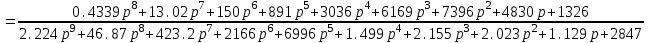 >> zpk(w) Zero/pole/gain: 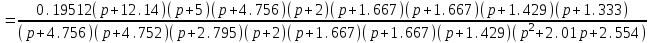 После сокращения получим: 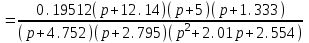 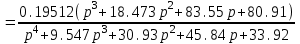 Степень астатизма: ν = 0. Коэффициент передачи: К=0.19512 ЗАДАНИЕ 2. Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики разомкнутой системы. W(iω)= 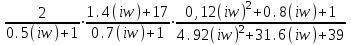 = = 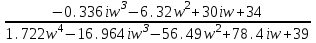 = =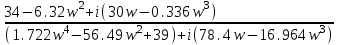 P( 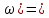 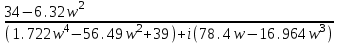 Q( 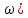 = = 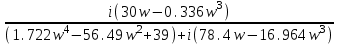 ЗАДАНИЕ 3. Построить годограф АФЧХ разомкнутой системы. >> nyquist(W) 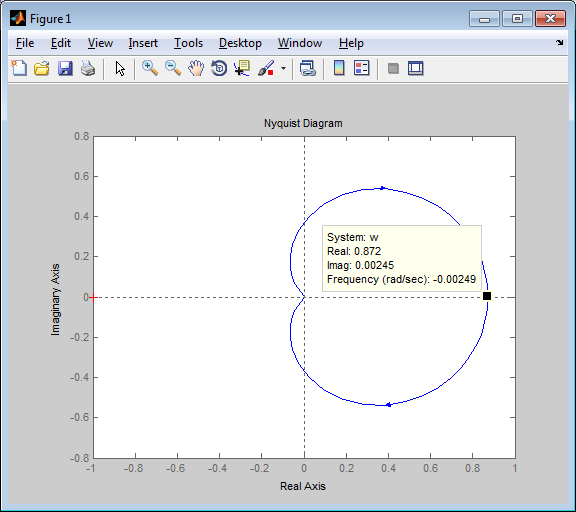 Годограф при ω=0 начинается на положительной вещественной полуоси. При ω→ ∞ через четвертый и третий квадранты стремится к нулю. Пересекает при ω=0 вещественную ось в точке (0.872;i0). ЗАДАНИЕ 4. Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы. Асимптотическая ЛАЧХ: L( 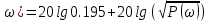 L( 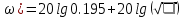 Асимптотическая ЛФЧХ: φ( 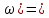 arctg(Q( arctg(Q(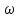 )) – arctg(P( )) – arctg(P(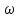 )) ))φ( 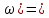 arctg( arctg(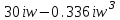 )-arctg( )-arctg(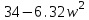 ) )ЗАДАНИЕ 5. Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы. >> bode(W) 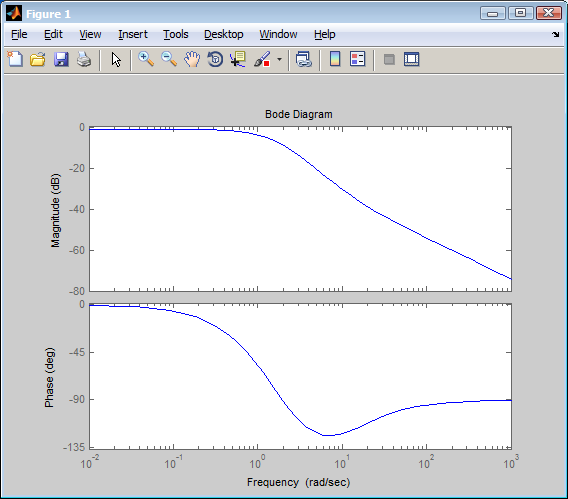 ЗАДАНИЕ 6. Определить устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик. » pole (W) ans = -4.7561 -4.7517 -2.7950 -1.0051 + 1.2423i -1.0051 - 1.2423i -2.0000 -1.6667 + 0.0000i -1.6667 - 0.0000i -1.4286 Так как степень астатизма системы ν=0 и характеристический полином разомкнутой системы имеет все корни в левой половине комплексной плоскости, то критерий Найквиста будет следующим: для того чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы не охватывал точку с координатами (-1; j0).  Как видно, годограф АФХ не охватывает эту точку. Следовательно, замкнутая система будет устойчивой. 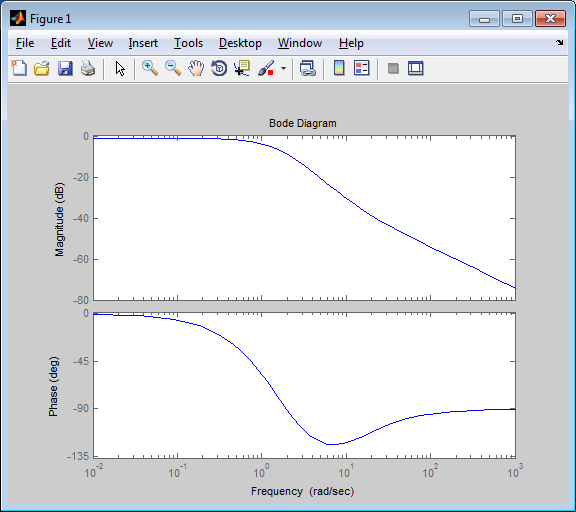 ЛАЧХ разомкнутой системы не пересекает линию 0 дБ и ЛФЧХ не пересекает линию -1800, значит замкнутая система будет устойчивой. ЗАДАНИЕ 7. Найти запасы устойчивости системы по фазе и по амплитуде.  » margin(W) 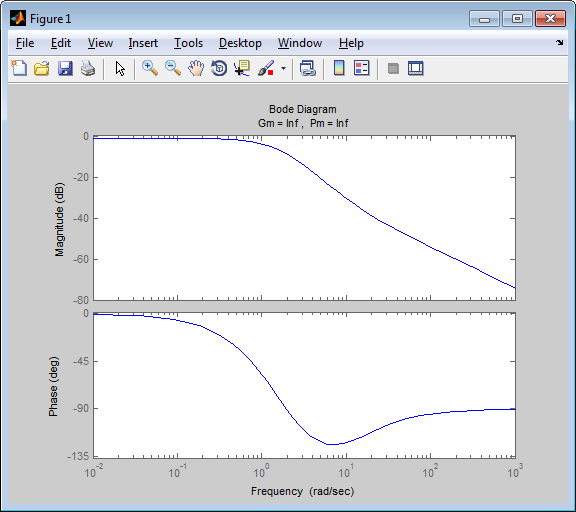 Как видно годограф не пересекает отрицательную вещественную полуось, следовательно, запас устойчивости по амплитуде такой системы равен 1. Значит А()=1. При наклоне характеристики равном 0 дБ/дек есть излишне большие запасы устойчивости по фазе. Так как, при любом , А()1, то замкнутая система не имеет угла, образуемого радиусом, проходящим через точку пересечения годографа Найквиста с окружностью единичного радиуса с центром в начале координат и отрицательной вещественной полуосью. ЗАДАНИЕ 8. Найти передаточную функцию замкнутой системы и проверить выводы пункта 6 с помощью частотного критерия Михайлова. >>feedback(W,1) Transfer function: 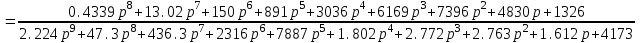 >> zpk(wz) Zero/pole/gain: 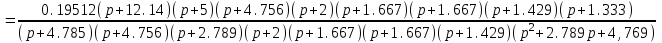 После сокращения получим: 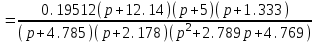 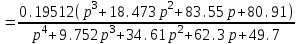 Характеристическое уравнение передаточной функции: D(p)= 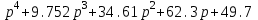  D(iw)= 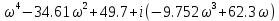 Вычислим корни вещественной и мнимой части: Вещественная часть: U(w)= 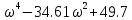 w1=5.754 w2=1.225 мнимая часть: V(w)= 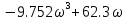 w1=0; w2= 2.53 Находим пересечения с осями: 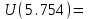 -0.01 -0.01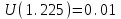 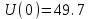 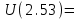 -130.86 -130.86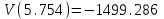 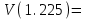 58.38 58.38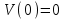 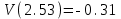
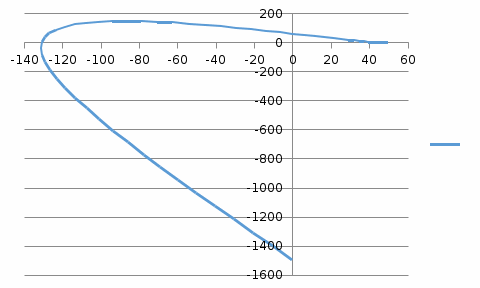 Из годографа видно, что система огибает начало координат против часовой стрелки последовательно n-квадрантов, следовательно, замкнутая система устойчива, что было подтверждено в пункте 6. ЗАДАНИЕ 9. Определить величину поправочного коэффициента усиления, при котором статическая ошибка замкнутой системы будет не больше 0.1; перерегулирование в системе составит 12 %; время переходного процесса будет минимальным. 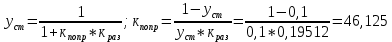 W 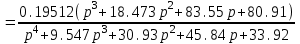 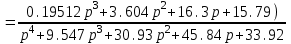 Wзс= feedback(W*46.125,1) Wзс=  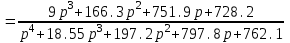 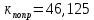 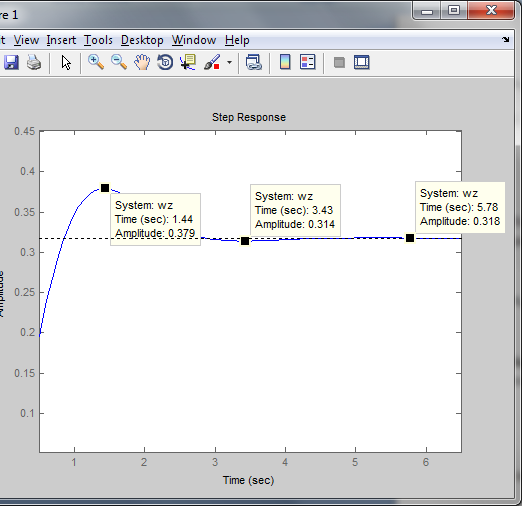 2) 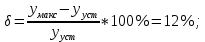 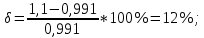 Чтобы перерегулирование в системе составило 12%, изменим коэффициент передачи в передаточной функции разомкнутой системы. W=  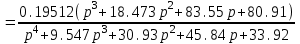 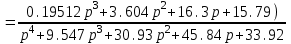 Wзс=feedback(W*180,1) Wзс= 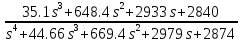 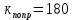 ; ;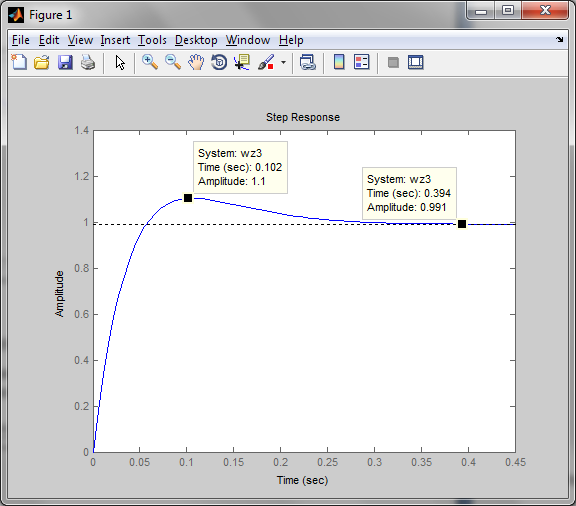 3) Wпц= 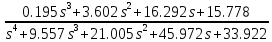 ; ;Wзс= 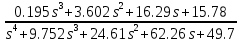 ; ;Поправочный коэффициент усиления, при минимальном времени переходного процесса (1,44) равен 46,154 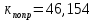 . .Задание 10. Построить с переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование и время регулирования) в системе. Wпц= 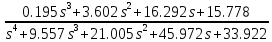 ; ;Wзс= 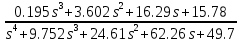 ; ; Основные показатели: Статистическая ошибка: 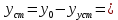 1-0,318=0,682 1-0,318=0,682Динамическая ошибка: 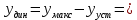 0,379-0,318=0,061 0,379-0,318=0,061Время регулирования: 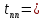 3.43 3.43Перерегулирование: 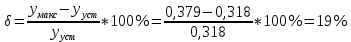 Литература Лекции по дисциплине: "Основы теории управления" / В.В.Гетман Анализ и синтез линейных систем автоматического управления: лабораторный практикум / В.В.Гетман, Н.В. Лежнева. - Казань: Изд-во Казан. Гос. Технол. Ун-та, 2007. - 64с. Методы синтеза линейных систем автоматического управления: методические указания к лабораторным работам / сост.: В.В.Гетман, Н.В. Лежнева. - Нижнекамск: Нижнекамский химико-технологический институт (филиал) КГТУ, 2010. -44 с. >> w=tf([2],[0.5,1]) Transfer function: 2 --------- 0.5 s + 1 >> w1=tf([2],[0.5,1]) Transfer function: 2 --------- 0.5 s + 1 >> w2=tf([2]) Transfer function: 2 >> w3=tf([0.2,1],[0.6,1]) Transfer function: 0.2 s + 1 --------- 0.6 s + 1 >> w4=tf([15],[0.7,1]) Transfer function: 15 --------- 0.7 s + 1 >> w=tf([19]) Transfer function: 19 >> w=tf([0.15,1],[0.75,1]) Transfer function: 0.15 s + 1 ---------- 0.75 s + 1 >> w5=tf([19]) Transfer function: 19 >> w6=tf([0.15,1],[0.75,1]) Transfer function: 0.15 s + 1 ---------- 0.75 s + 1 >> w7=w2+w4 Transfer function: 1.4 s + 17 ---------- 0.7 s + 1 >> w8=w3/(1+w2*w3*w5) Transfer function: 0.12 s^2 + 0.8 s + 1 ---------------------- 4.92 s^2 + 31.6 s + 39 >> wraz=(w1*w7*w8)/(1+w1*w6*w7*w8) Transfer function: 0.4339 s^8 + 13.02 s^7 + 150 s^6 + 891 s^5 + 3036 s^4 + 6169 s^3 + 7396 s^2 + 4830 s + 1326 ---------------------------------------------------------------------------------------------------------------------------- 2.224 s^9 + 46.87 s^8 + 423.2 s^7 + 2166 s^6 + 6996 s^5 + 1.499e004 s^4 + 2.155e004 s^3 + 2.023e004 s^2 + 1.129e004 s + 2847 >> zpk(wraz) Zero/pole/gain: 0.19512 (s+12.14) (s+5) (s+4.756) (s+2) (s+1.667)^2 (s+1.429) (s+1.333) ------------------------------------------------------------------------------- (s+4.756) (s+4.752) (s+2.795) (s+2) (s+1.667)^2 (s+1.429) (s^2 + 2.01s + 2.554) >> nyquist(wraz) >> bode(wraz) >> pole(wraz) ans = -4.7561 -4.7517 -2.7950 -1.0051 + 1.2423i -1.0051 - 1.2423i -2.0000 -1.6667 + 0.0000i -1.6667 - 0.0000i -1.4286 >> margin(wraz) >> feedback(wraz,1) Transfer function: 0.4339 s^8 + 13.02 s^7 + 150 s^6 + 891 s^5 + 3036 s^4 + 6169 s^3 + 7396 s^2 + 4830 s + 1326 --------------------------------------------------------------------------------------------------------------------------- 2.224 s^9 + 47.3 s^8 + 436.3 s^7 + 2316 s^6 + 7887 s^5 + 1.802e004 s^4 + 2.772e004 s^3 + 2.763e004 s^2 + 1.612e004 s + 4173 >> wz=feedback(wraz,1) Transfer function: 0.4339 s^8 + 13.02 s^7 + 150 s^6 + 891 s^5 + 3036 s^4 + 6169 s^3 + 7396 s^2 + 4830 s + 1326 --------------------------------------------------------------------------------------------------------------------------- 2.224 s^9 + 47.3 s^8 + 436.3 s^7 + 2316 s^6 + 7887 s^5 + 1.802e004 s^4 + 2.772e004 s^3 + 2.763e004 s^2 + 1.612e004 s + 4173 >> zpk(wz) Zero/pole/gain: 0.19512 (s+12.14) (s+5) (s+4.756) (s+2) (s+1.667)^2 (s+1.429) (s+1.333) -------------------------------------------------------------------------------- (s+4.785) (s+4.756) (s+2.178) (s+2) (s+1.667)^2 (s+1.429) (s^2 + 2.789s + 4.769) >> w1=tf([1,4.785]) Transfer function from input 1 to output: 1 Transfer function from input 2 to output: 4.785 >> w=wz*46.125 Transfer function: 20.02 s^8 + 600.4 s^7 + 6917 s^6 + 4.11e004 s^5 + 1.4e005 s^4 + 2.846e005 s^3 + 3.411e005 s^2 + 2.228e005 s + 6.116e004 --------------------------------------------------------------------------------------------------------------------------- 2.224 s^9 + 47.3 s^8 + 436.3 s^7 + 2316 s^6 + 7887 s^5 + 1.802e004 s^4 + 2.772e004 s^3 + 2.763e004 s^2 + 1.612e004 s + 4173 >> step(w) >> |
