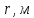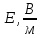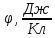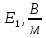РГЗ по Электростатике, Горный университет, 10 вариант. ргз физика левчук. Должность) (подпись) (Ф. И. О
 Скачать 262.58 Kb. Скачать 262.58 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра общей и технической физики РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ по разделу Электростатика Вариант 10 По дисциплине: Физика (наименование учебной дисциплины согласно учебному плану) Автор: студент гр. ВД-21 Левчук А.А. (шифр группы) (подпись) (Ф.И.О.) Дата: Проверил: Иванов А. С. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 Условия заданий 1.1 Рассчитать напряженность и потенциал электростатического поля, равномерно заряженной заряд 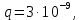 сферической радиусом сферической радиусом 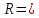 7 см, поверхности для точек внутри сферы, на ее поверхности и вне сферы на заданных расстояниях 7 см, поверхности для точек внутри сферы, на ее поверхности и вне сферы на заданных расстояниях 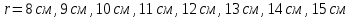 от ее центра. от ее центра.Построить графики зависимостей напряженности и потенциала от расстояния от центра сферы для обеих сред. 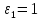 , , 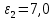 С помощью силовых линий вектора напряженности графически изобразить электростатическое поле равномерно заряженной сферы и доказать, что аналитическое представление электростатического поля совпадает с графическим. 1.2 Шар радиусом 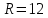 см равномерно заряжен с объемной плотностью см равномерно заряжен с объемной плотностью 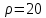 нКл/м3. нКл/м3.Используя теорему Остроградского - Гаусса, вывести формулу зависимости напряженности электрического поля E от расстояния r от центра шара для случая, когда r Построить график зависимости 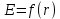 для случая, когда для случая, когда 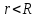 . .Определить разность потенциалов между двумя точками, лежащими внутри шара на расстояниях 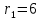 см и см и 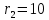 см от его центра. см от его центра.1.3 Две коаксиальные цилиндрические поверхности 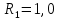 см и см и 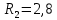 см (цилиндрический конденсатор) заряжены разноименно с одинаковой линейной плотностью см (цилиндрический конденсатор) заряжены разноименно с одинаковой линейной плотностью 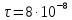 Кл/м. Кл/м. Рассчитать напряженность электрического поля E на расстояниях 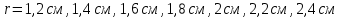 от оси цилиндров. от оси цилиндров.Построить графики зависимости напряженности электрического поля от расстояния от оси цилиндров, если пространство между цилиндрами заполнено: а) воздухом, 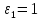 б) диэлектриком б) диэлектриком 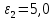 1.4 Электростатическое поле создано двумя бесконечными параллельными плоскостями (пластинами), равномерно заряженными с поверхностными плотностями заряда 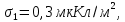 и и 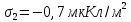 . Расстояние между плоскостями равно . Расстояние между плоскостями равно 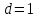 см. см.Найти разность потенциалов между пластинами. Определить напряженность электростатического поля между пластинами и вне пластин. Построить график изменения напряженности электростатического поля вдоль линии, перпендикулярной пластинам. 2. Решение задач расчётно-графической работы Задача 1.1 1. Вывод формул напряжённости поля: С одной стороны, по определению потока вектора напряженности через поверхность сферы: 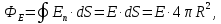 так как линии напряженности перпендикулярны поверхности сферы. так как линии напряженности перпендикулярны поверхности сферы. С другой стороны, по теореме Гаусса для равномерно заряженной сферы с общим зарядом Q: 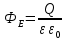 . .В результате получим формулу напряженности для точки лежащей на поверхности сферы 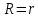 , где r – расстояние от центра сферы до рассматриваемой точки: , где r – расстояние от центра сферы до рассматриваемой точки: 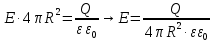 . .Для точки, лежащей внутри сферы ( 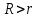 ), ), 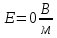 , так как по условию заряд распределен на поверхности сферы. , так как по условию заряд распределен на поверхности сферы.Для точки, которая лежит вне сферы ( 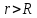 ): ):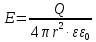 2. Вывод формул потенциала поля: По определению потенциала для равномерно заряженной сферы с общим зарядом Q вне сферы ( 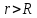 ): ): 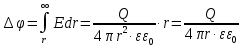 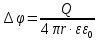 Внутри сферы при 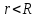 , как было написано выше, поле отсутствует, следовательно потенциал постоянен. Он равен тому значению, которое имел на ее поверхности: , как было написано выше, поле отсутствует, следовательно потенциал постоянен. Он равен тому значению, которое имел на ее поверхности: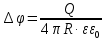 3. Подставим имеющиеся данные и рассчитаем напряженность и потенциал для двух сред: Пример расчета напряженности поля для для 1 = 1 при 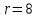 см: см: 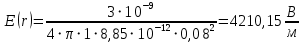 Пример расчета потенциала поля для для 1 = 1 при 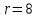 см: см: 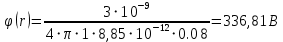 Аналогично проведены расчеты для остальных значений r, представленных в таблице 1. Таблица 1. Значения напряженности и потенциала поля равномерно заряженной сферы, помещенной в среду с 1 = 1, в зависимости от r
Пример расчета напряженности поля для для 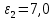 , при , при 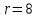 см: см: 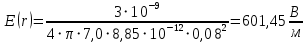 Пример расчета потенциала поля для для 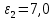 при при 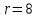 см: см: 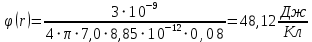 Аналогично проведены расчеты для остальных значений r, представленных в таблице 2. Таблица 2. Значения напряженности и потенциала поля равномерно заряженной сферы, помещенной в среду с 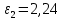 , в зависимости от r. , в зависимости от r.
4. Графическое изображение зависимостей напряженности и потенциала от расстояния от центра сферы для обеих сред. 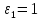 , , 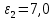 : : Рисунок 1. Зависимость 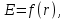 при при 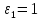 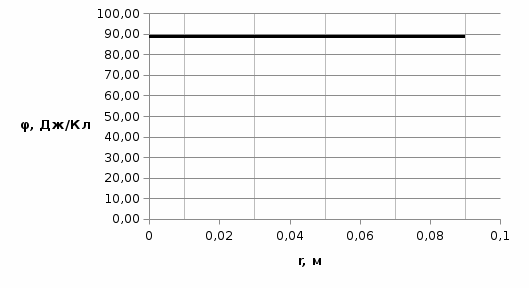 Рисунок 2. Зависимость 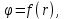 при при   Рисунок 3. Зависимость 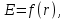 при при 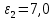 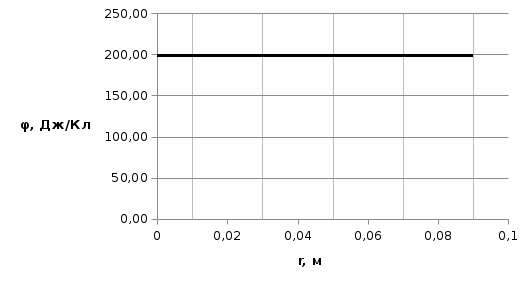 Рисунок 4. Зависимость φ = f(r), при 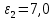 Зависимость E(r) и φ(r) от обратно пропорциональная, потому чем больше диэлектрическая проницаемость, тем меньше напряжённость электрического поля и его потенциал. 5 E, В/м . Графическое изображение электростатического поля равномерно заряженной сферы: 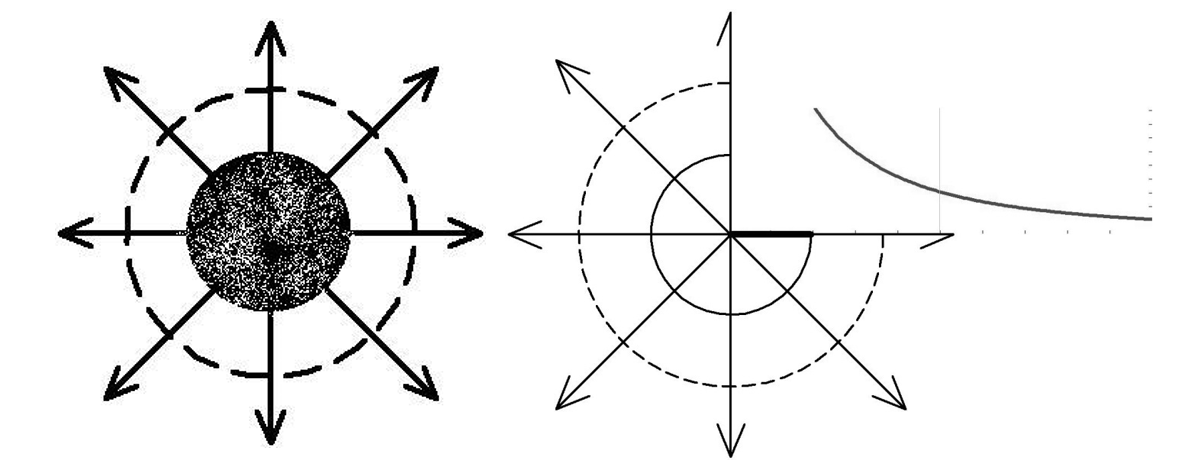 r, м Рисунок 5. Графическое изображение электростатического поля равномерно заряженной сфера Линии напряженности направлены по линии радиуса шара и соответственно, чем дальше от источника, тем меньше плотность силовых линий, а значит и меньше напряжённость. Аналитическое представление электростатического поля совпадает с графическим. Задача 1.2 1. Вывод формул напряжённости поля: С одной стороны, по определению потока вектора напряженности через равномерно заряженный шар объемной плотность 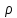 и r и r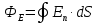 = = 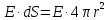 С другой стороны, по теореме Гаусса для равномерно заряженного шара объемной плотность 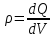 и и 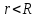 : в связи с тем, что сфера радиуса r>R охватывает заряд : в связи с тем, что сфера радиуса r>R охватывает заряд 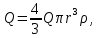 то поток вектора напряженности будет равен то поток вектора напряженности будет равен 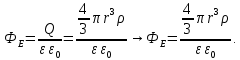 В результате получим формулу напряженности для точки, лежащей внутри шара, на расстоянии 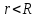 : :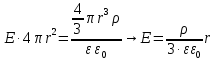 2. Вывод формул потенциала поля: Разность потенциалов между двумя точками, лежащими на расстоянии 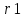 и и 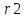 от центра объемно заряженного шара с общим зарядом Q ( от центра объемно заряженного шара с общим зарядом Q (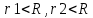 ): ): 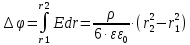 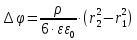 3. Подставим имеющиеся данные и рассчитаем напряженность и потенциал: Пример расчета напряженности поля для для = 1, при 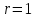 см: см: 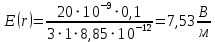 Аналогично проведены расчеты для остальных значений r, представленных в таблице 3. 4. Расчет потенциала между двумя точками, лежащими внутри шара на расстояниях 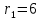 см и см и 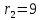 см от его центра: см от его центра: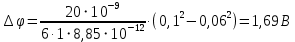 Таблица 3. Значения напряженности поля объемно заряженного шара с общим зарядом Q в зависимости от 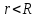
5. Графическое изображение зависимости напряженности от расстояния от центра шара, для случая 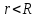 : :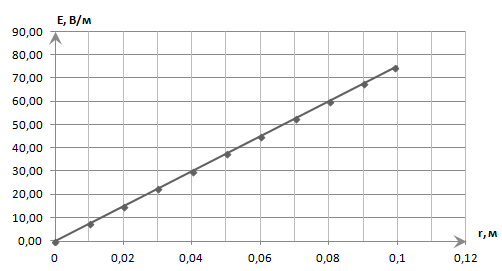 Рисунок 6. Зависимость 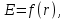 при при 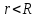 . .Таким образом, напряженность поля шара находится в прямой (линейной) зависимости от расстояния от его центра, когда 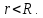 Задача 1.3 1. Вывод формул напряжённости поля: С одной стороны, по определению потока вектора напряженности через коаксиальный цилиндр с линейной плотность 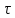 , высотой , высотой 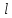 и и 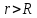 , поток вектора сквозь торцы коаксиального цилиндра равен нулю, т.к. торцы параллельны линиям напряженности, а сквозь боковую поверхность: , поток вектора сквозь торцы коаксиального цилиндра равен нулю, т.к. торцы параллельны линиям напряженности, а сквозь боковую поверхность: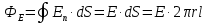 С другой стороны, по теореме Гаусса для коаксиального цилиндра с линейной плотность 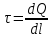 , высотой , высотой 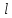 и и 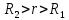 , с учетом того что, , с учетом того что, 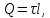 то поток вектора напряженности будет равен то поток вектора напряженности будет равен 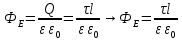 В результате получим формулу напряженности для коаксиального цилиндра, 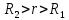 : :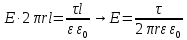 2. Подставим имеющиеся данные и рассчитаем напряженность для двух сред: Пример расчета напряженности поля для для 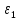 = 1, при = 1, при 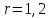 см: см: 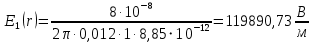 Пример расчета напряженности поля для для 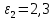 , при , при 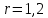 см: см: 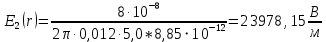 Аналогично проведены расчеты для остальных значений r, представленных в таблице 4. Таблица 4. Значения напряженности поля коаксиального цилиндра в зависимости от расстояния до центра в воздухе и диэлектрике, 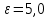 , ,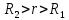
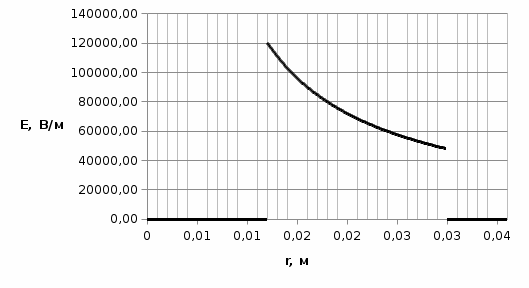 Рисунок 7. Зависимость 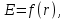 при при 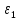 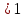 . .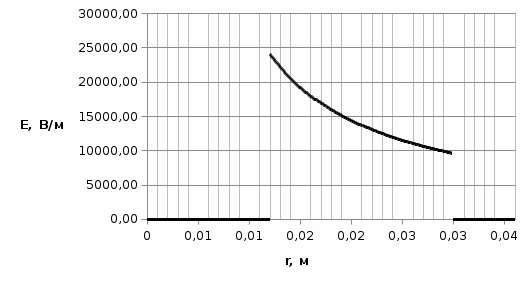 Рисунок 8. Зависимость 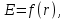 при при 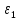 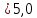 . .Таким образом, напряженность обратно пропорциональна расстоянию от оси коаксиальных цилиндров, при этом внутри внутреннего цилиндра напряженность будет равна нулю, как и за пределами внешнего из цилиндров. Задача 1.4 1. Вывод формул напряжённости поля: Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности 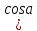 =0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания =0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания 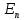 совпадает с Е): совпадает с Е):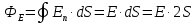 С другой стороны, по теореме Гаусса для бесконечно заряженной плоскости с поверхностной плотностью 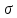 , с учетом того что, , с учетом того что, 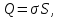 то поток вектора напряженности будет равен: то поток вектора напряженности будет равен: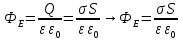 В результате получим формулу напряженности для бесконечно заряженной плоскости: 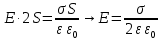 Рассмотрим две бесконечно параллельные одноименно заряженные плоскости. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Слева и справа от плоскостей поля складываются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля: 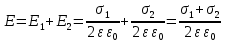 Причем, напряженности слева и справа будут различаться знаками. В области между плоскостями: 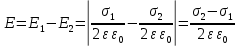 2. Вывод формул потенциала поля: Разность потенциалов между двумя плосокстями, расстояние между которыми равно 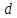 : :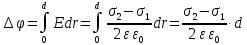 3. Подставим имеющиеся данные и рассчитаем напряженность и потенциал для двух плоскостей: Расчет напряженности поля слева и справа от плоскостей: 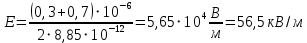 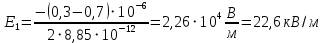 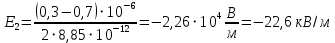 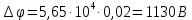 4. Графическое изображение изменения напряженности электростатического поля вдоль линии, перпендикулярной пластинам: 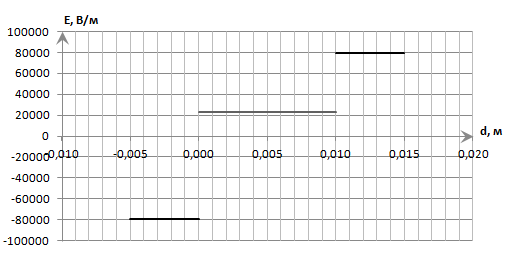 Рисунок 9. Изменение напряженности электростатического поля вдоль линии, перпендикулярной пластинам Вид графика подтверждает аналитические формулы. Напряженность поля на любых расстояниях одинакова по модулю, таким образом поле равномерно заряженной бесконечной плоскости однородно. |