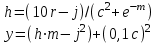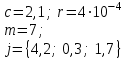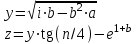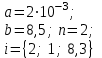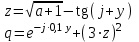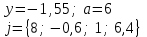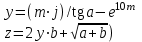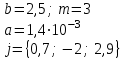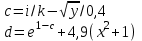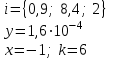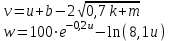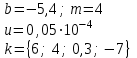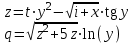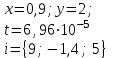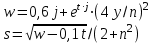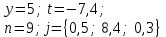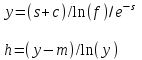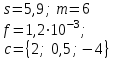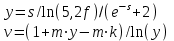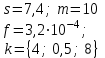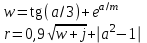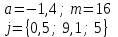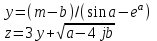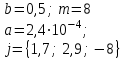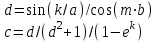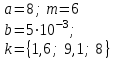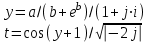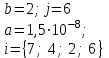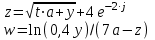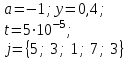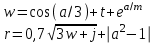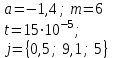ДОМАШНЕЕ ЗАДАНИЕ ПОСЛЕ ЛАБОРАТОРНОЙ РАБОТЫ 1
В соответствии со своим вариантом написать консольную программу по условиям, приведенным в таблице ниже.
№ варианта
|
Условие задачи
|
1
|
Ввести три числа m, n, p. Подсчитать количество отрицательных чисел.
|
2
|
Определить, имеется ли среди трёх чисел a, b и c хотя бы одна пара равных между собой чисел.
|
3
|
Даны три числа a, b и c. Найти среднее геометрическое этих чисел, если все они отличны от нуля, и среднее арифметическое в противном случае.
|
4
|
По номеру месяца напечатать пору года.
|
5
|
Определить, есть ли среди заданных целых чисел A, B, C, D хотя бы одно нечётное.
|
6
|
Дано натуральное трехзначное число n. Верно ли, что среди его цифр есть 0 или 9?
|
7
|
В переменную Y ввести номер года. Определить, является ли год високосным.
|
8
|
Дано натуральное четырехзначное число n. Верно ли, что все его цифры различны?
|
9
|
Проверить, является ли дробь A / B правильной.
|
10
|
Число делится на 3 тогда, когда сумма его цифр делится на 3. Проверить этот признак на примере заданного трехзначного числа.
|
11
|
Даны три числа a, b, c. Значение наибольшего из них присвоить переменной d.
|
12
|
Есть натуральное двузначное число n. Верно ли, что среди его цифр есть 1 или 9?
|
13
|
Для натурального числа К напечатать фразу «мы нашли К грибов в лесу», согласовав окончание слова «гриб» с числом К.
|
14
|
Для целого числа К от 1 до 9 напечатать фразу «мне К лет», учитывая при этом, что при некоторых значениях К слово «лет» надо заменить на слово «год» или «года».
|
15
|
Определить есть ли среди заданных целых чисел A, B, C, D хотя бы одно чётное.
|
16
|
По введенному числу (от 0 до 7) напечатать название цифры.
|
Задание 2
В таблице приведены формулы и три варианта исходных данных, по которым надо разработать три циклические программы с одними и теми же расчетными формулами.
При наличии ошибок из-за некорректных исходных данных выполнить вычисления с другими числами.
№
|
Формулы для вычислений
|
Исходные данные
(for)
|
Исходные данные
(while)
|
Исходные данные
(двойной цикл)
|
1
|
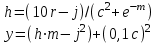
|
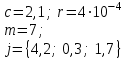
|
j = 0(0,1)1,7
|
j = {9; 1,8; 15; -3},
m = 1(0,5)2
|
2
|
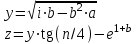
|
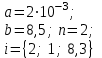
|
i = 1(0,5)3
|
b = 2(0,5)3,
n = {3; 6; 0,2; 2,8}
|
3
|
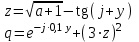
|
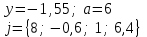
|
j = 1(0,2)1
|
a = 1(0,2)2,
y = {3,3; 4; 0,9}
|
4
|
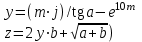
|
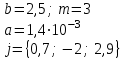
|
j = b(0,1)3
|
m = {7,3; 2; 0,8},
y = {0,3; 1; 0,7; 4}
|
5
|
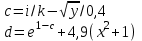
|
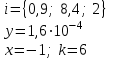
|
i = 0(0,5)3
|
x = 1(0,1)2,
y = {1,3; 8; 0,2}
|
6
|
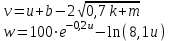
|
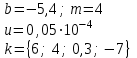
|
k = 3(0,2)4
|
b = 7(0,2)8,
m = {1,3; 2; 4,9}
|
7
|
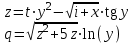
|
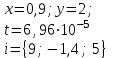
|
i = 1(0,2)2
|
t = 2(0,2)3,
x = {0,7; 1; 9}
|
8
|
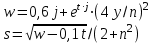
|
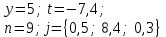
|
j = 0(0,1)2
|
y = {0,1; 3; 0,5},
j = 0,1(0,1)0,4
|
9
|
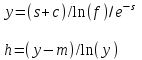
|
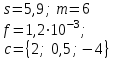
|
c = 0(0,1)0,9
|
s = { 3; 0,8; 4},
c = 0,2(0,1)0,5
|
10
|
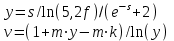
|
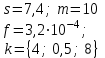
|
k = 0(0,5)4
|
k = {0,9; 11; 0,5},
m = 0,3(0,1)0,7
|
11
|
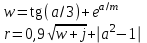
|
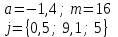
|
j = 1,8(0,2)3
|
a = {0,2; 4; 0,6},
j = 0,1(0,1)0,4
|
12
|
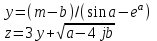
|
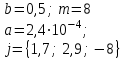
|
j = 2(0,5)3
|
b = 2(0,5)3,
m = {0,4; 1; 1,9}
|
13
|
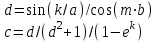
|
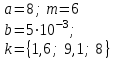
|
k = a(0,5)3
|
a = 2(0,2)2,8,
x = {1,7; 5; 2}
|
14
|
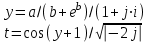
|
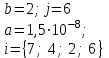
|
i = 3(0,1)2
|
b = 2,4(0,2)3,
a = {0,1; 1; 3}
|
15
|
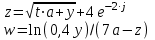
|
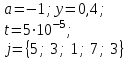
|
j = 1(0,2)2
|
t = 3(0,2)4,
a = {0,2; 1,6; 9,4}
|
16
|
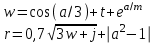
|
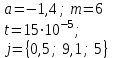
|
j = 1(0,1)2
|
m = 8(0,2)9,
x = {0,6; 0,1; 5}
|
Задание 3
1. Шестизначный автобусный билет считается удачным, если сумма его цифр делится на 7. Могут ли два билета подряд быть удачными?
2. Торговая фирма в первый день работы реализовала товаров на P тыс. руб., а затем ежедневно увеличивала выручку на 3%. Какой будет выручка фирмы в тот день, когда она впервые превысит заданное значение Q? Сколько дней придется торговать фирме для достижения этого результата?
3. О каждом учащемся класса известны его пол, год рождения, рост и вес. Определить, сколько в классе мальчиков и сколько девочек. Найти средний возраст мальчиков и девочек. Определить, верно ли, что самый высокий мальчик весит больше всех в классе, а самая маленькая девочка является самой юной среди девочек.
4. Фирма ежегодно на протяжении n лет закупала оборудование стоимостью соответственно s1, s2, ..., sn pублей в год (эти числа вводятся и обрабатываются последовательно). Ежегодно в результате износа и морального старения (амортизации) все имеющееся оборудование уценивается на р%. Какова общая стоимость накопленного оборудования за n лет?
5. Дана непустая последовательность ненулевых целых чисел, за которой следует 0. Определить, сколько раз в этой последовательности меняется знак.
6. Выполнить задание без хранения последовательностей. Дано натуральное k. Определить k-ю цифру последовательности: 1248163264 ..., в которой выписаны подряд степени 2.
7. Составить алгоритм решения ребуса КОТ + КОТ = ТОК (различные буквы означают различные цифры, старшая буква ‒ не 0).
8. Натуральное число, записанное в десятичной системе счисления, называется сверхпростым, если оно остается простым при любой перестановке своих цифр. Определить все сверхпростые числа до n.
Задание 4
Сформировать одномерный список целых чисел A, используя генератор случайных чисел (диапазон от 0 до 99). Размер списка n ввести с клавиатуры. В соответствии со своим вариантом написать программу по условию, представленному в таблице ниже.
№ варианта
|
Условие задачи
|
1
|
Удалить элемент с введенным номером a.
|
2
|
Все четные по значению элементы исходного списка A поместить в новый список B.
|
3
|
Удалить элементы, индексы которых кратны 7.
|
4
|
Найти значение минимального элемента списка.
|
5
|
Для каждого четного по номеру элемента списка A найти его сумму со следующим элементом и записать эти суммы в новый список B.
|
6
|
Удалить все элементы с заданным значением, если они имеются в списке.
|
7
|
Удалить из списка все элементы, совпадающие с его минимальным значением.
|
8
|
Найти значение максимального элемента списка.
|
9
|
Найти среднее арифметическое элементов списка.
|
10
|
Найти среднее арифметическое трех последних элементов списка.
|
11
|
Удалить пять первых нечетных по значению элементов списка.
|
12
|
Найти номер минимального элемента списка.
|
13
|
Найти для каждого элемента списка А сумму предыдущих элементов и записать эти суммы в новый список B.
|
14
|
Найти индексы первого и последнего нулевых элементов списка.
|
15
|
Удалить элементы, индексы которых кратны 3.
|
16
|
Найти номера минимального и максимального элементов первой половины списка.
| |
 Скачать 62.95 Kb.
Скачать 62.95 Kb.