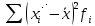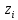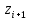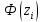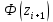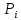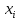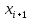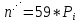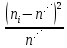Главная страница
Навигация по странице:

  • Итого 59

  • Итого 59 11030,1

  • 59,00 59,00 10,27

    		•

    статистика. Домашняя работа по Статистике исправл. Домашняя работа по Статистике


    Скачать 55.7 Kb.
    НазваниеДомашняя работа по Статистике
    Анкорстатистика
    Дата26.01.2022
    Размер55.7 Kb.
    Формат файлаdocx
    Имя файлаДомашняя работа по Статистике исправл.docx
    ТипРешение
    #342274
    страница2 из 2
    1   2

    По каждой группе определим число единиц – частоты, середину интервала и накопленные частоты

    Группы
    Середина интервала
    Частота

    Накопленные частоты

    98-126,6
    112,3
    9
    9

    126,6-155,2
    140,9
    4
    13

    155,2-183,8
    169,5
    11
    24

    183,8-212,4
    198,1
    21
    45

    212,4-241
    226,7
    8
    53

    241-269,6
    255,3
    3
    56

    269,6-298
    283,9
    3
    59

    Итого




    59



    3.Построить полигон частот, гистограмму

    Полигон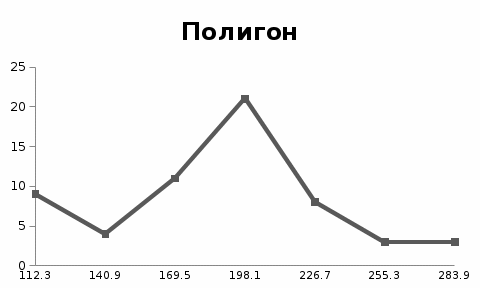



    Гистограмма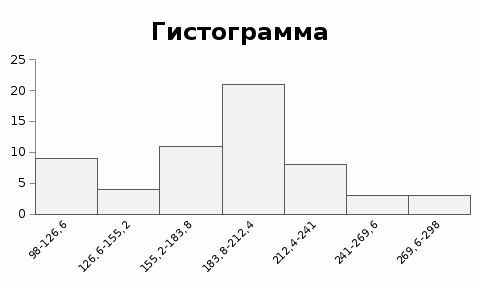


    4.Найти и построить функцию распределения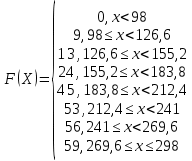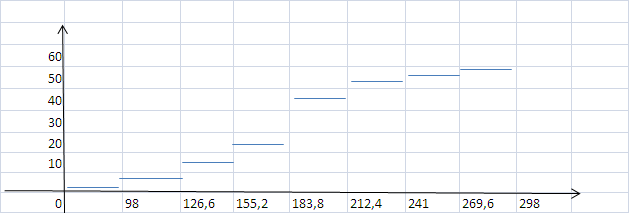



    5.Найти математическое ожидание, дисперсию, ско

    Математическое ожидание (среднее значение) определим по формуле средней арифметической взвешенной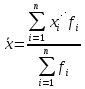



    где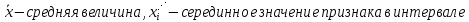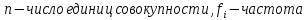



    Дисперсия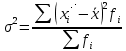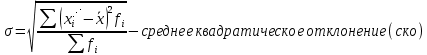



    Расчетная таблица

    Группы
    Середина интервала
    Частота

    xf
     

    98-126,6
    112,3
    9
    1010,7
    63958,4

    126,6-155,2
    140,9
    4
    563,6
    12410

    155,2-183,8
    169,5
    11
    1864,5
    8078,51

    183,8-212,4
    198,1
    21
    4160,1
    47,25

    212,4-241
    226,7
    8
    1813,6
    7248,08

    241-269,6
    255,3
    3
    765,9
    10337,1

    269,6-298
    283,9
    3
    851,7
    22863,9

    Итого

     
    59
    11030,1
    124943

    Получаем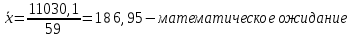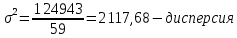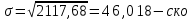






    6.Найдем внутригрупповую и межгрупповую дисперсии

    Определим вначале внутригрупповые дисперсии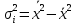



    Группы
    X
    X2

    98-126,6
    98
    9604

    98
    9604

    98
    9604

    103
    10609

    105
    11025

    107
    11449

    117
    13689

    125
    15625

    126
    15876

    итого по группе
    977
    107085

    ср.знач.
    108,56
    11898,33

    внутр.дисп.
    114,02



    126,6-155,2
    134
    17956

    137
    18769

    137
    18769

    149
    22201

    итого по группе
    557
    77695

    ср.знач.
    139,25
    19423,75

    внутр.дисп.
    33,1875



    155,2-183,8
    156
    24336

    156
    24336

    160
    25600

    165
    27225

    166
    27556

    166
    27556

    173
    29929

    176
    30976

    176
    30976

    181
    32761

    182
    33124

    итого по группе
    1857
    314375

    ср.знач.
    168,82
    28579,55

    внутр.дисп.
    79,97



    183,8-212,4
    184
    33856

    186
    34596

    186
    34596

    188
    35344

    192
    36864

    194
    37636

    196
    38416

    196
    38416

    196
    38416

    196
    38416

    199
    39601

    200
    40000

    201
    40401

    204
    41616

    205
    42025

    205
    42025

    205
    42025

    205
    42025

    205
    42025

    211
    44521

    212
    44944

    итого по группе
    4166
    827764

    ср.знач.
    198,38
    39417,33

    внутр.дисп.
    62,33



    212,4-241
    214
    45796

    215
    46225

    220
    48400

    222
    49284

    225
    50625

    228
    51984

    234
    54756

    235
    55225

    итого по группе
    1793
    402295

    ср.знач.
    224,125
    50286,875

    внутр.дисп.
    54,86



    241-269,6
    245
    60025

    245
    60025

    254
    64516

    итого по группе
    744
    184566

    ср.знач.
    248
    61522

    внутр.дисп.
    18



    269,6-298
    274
    75076

    284
    80656

    298
    88804

    итого по группе
    856
    244536

    ср.знач.
    285,33
    81512

    внутр.дисп.
    96,89




    Находим среднюю из групповых дисперсий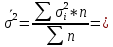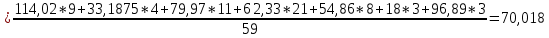





    Межгрупповая дисперсия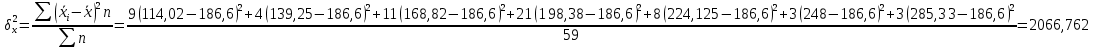



    Общая дисперсия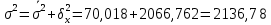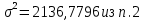





    Разница в вычислениях в результате округления результатов.

    7.Моду и медиану (для сгруппированных и для не сгруппированных данных)

    Для сгруппированных данных

    Мода для интервального ряда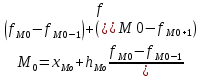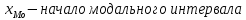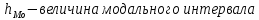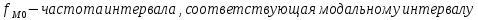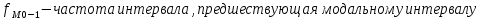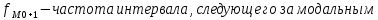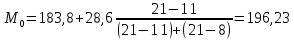















    Медианный размер определяем по формуле для интервального ряда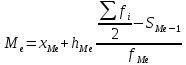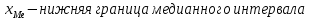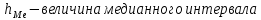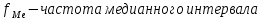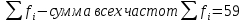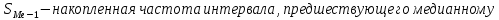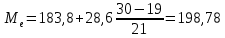















    Для несгруппированных данных

    Мода – варианта с наибольшей частотой из таблицы зад.1 наибольшая частота 5 соответствует значению 205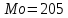



    Медиана середина ранжированного ряда.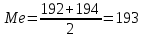



    8.Найдем интервальные оценки математического ожидания

    Определим ошибку выборки при вероятности 0,95 (t=1,96)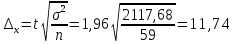



    Интервальные оценки математического ожидания при вероятности 0,997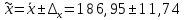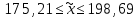





    9. Проверим гипотезу о том, что х распределено по нормальному закону, с помощью критерия Пирсона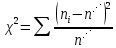



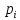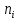    где – теоретическая вероятность попадания случайной величины в i-й интервал

    - частота (количество элементов совокупности, попавших в i-й интервал)

    Для вычисления вероятности, применим формулу: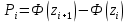



    где Ф – функция Лапласа

    z – нормированное значение случайной величины

    Для вычисления значения случайной величины левой и правой границы j-го интервала применим формулы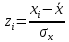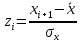





    Используя формулы и таблицу значений интегральной функции Лапласа построим таблицу

    Расчетная таблица

    № интервала
    Границы интервала, xj














    1
    98
    126,6
    -
    -1,31
    -0,5
    -0,4049
    0,0951

    2
    126,6
    155,2
    -1,31
    -0,69
    -0,4049
    -0,2549
    0,15

    3
    155,2
    183,8
    -0,69
    -0,07
    -0,2549
    -0,0279
    0,227

    4
    183,8
    212,4
    -0,07
    0,55
    -0,0279
    0,2088
    0,2367

    5
    212,4
    241
    0,55
    1,17
    0,2088
    0,379
    0,1702

    6
    241
    269,6
    1,17
    1,80
    0,379
    0,4641
    0,0851

    7
    269,6
    298
    1,80
    -
    0,4641
    0,5
    0,0359

    Сравним теоретические и эмпирические частоты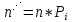




    5,61
    9
    2,047

    8,85
    4
    2,658

    13,39
    11
    0,428

    13,97
    21
    3,544

    10,04
    8
    0,415

    5,02
    3
    0,813

    2,12
    3
    0,367

    59,00
    59,00
    10,27

    В результате получаем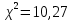

    Находим число степеней свободы, по формуле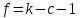



    где 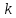- число интервалов выборки.

    Учитывая, что для закона нормального распределения с=2, находим числовое значение: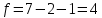



    Используя таблицу критических точек распределения Пирсона определяем, что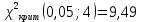



    Так как 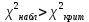, то гипотезу о нормальном распределении генеральной совокупности не принимаем. Эмпирические и теоретические частоты отличаются значимо.

    Вывод: данная выборка не имеет нормальное распределение.
    1   2

    написать администратору сайта