Курсовая. Курсова Саміленко В.О. кінцева (3). Дослідження методів інтерполяції
 Скачать 370.58 Kb. Скачать 370.58 Kb.
|
|
Вінницький національний технічний університет Кафедра автоматизації та інтелектуальних інформаційних технологій Факультет КСА КУРСОВА РОБОТА з дисципліни «Методи комп’ютерних обчислень» на тему: «Дослідження методів інтерполяції» Студента 2 курсу групи 2ІСТ-18б, напряму підготовки: 126 Інформаційні системи та технологоії Саміленко В.О.____________________ Керівник: к.т.н., доц. Богач І. В.__________________ Національна шкала ___________________ Кількість балів: _____ Оцінка: ECTS ____ Члени комісії: ___________________________ ___________________________ м. Вінниця – 2020 Міністерство освіти і науки України Вінницький національний технічний університет Факультет комп’ютерних систем і автоматики ЗАТВЕРДЖУЮ Зав. кафедри АІІТ, проф., д.т.н. ______________ Р.Н.Квєтний (підпис) „___” ______________ 2020 р. ІНДИВІДУАЛЬНЕ ЗАВДАННЯ на курсову роботу з дисципліни ”Методи комп'ютерних обчислень” студенту Саміленку В.О. групи 2ІСТ-18б ТЕМА Дослідження методів інтерполяції Постановка задачі: Дослідити чисельні методи розв’язання задачі інтерполяції Скласти алгоритми заданих методів Розробити програмне забезпечення для розв’язання інтерполяції напруги (кожен метод реалізувати окремою функцією) Протестувати програму Вирішити задану інтерполяцію, проаналізувати отримані результати, розрахувати похибки. Вхідні дані: початкові значення: методи для вирішення інтерполяції: методом Лагранжа та Ньютона (праві та ліві різниці); крок обчислення: тарировочна таблиця  Зміст пояснювальної записки до курсової роботи: Індивідуальне завдання Вступ 1. Короткі теоретичні відомості 2. Алгоритми методів 3. Розробка програмного забезпечення (вибір мови програмування; вхідні/ вихідні дані; структура програми; інструкція користувачеві) 4. Тестування програмного забезпечення 5. Аналіз отриманих результатів Висновки Перелік посилань Додатки (схема програми, лістинг програми та додаткові, за необхідністю) Дата видачі ”____” _________ 2020 р. Керівник _________________ (підпис) Завдання отримав _________ (підпис) АНОТАЦІЯ В даній курсовій роботі досліджено методи інтерполяції. Найбільшу увагу приділено обчисленню інтерполяції методами Лагранжа та Ньютона (праві та ліві різниці), розроблено та протестовано програмне забезпечення згідно з відповідними алгоритмами і обчисленно інтерполяцію та розраховується похибка. Ключові слова: інтерполяція, метод Лагранжа, метод Ньютона. ANNOTATION In this course work the methods of interpolation are investigated. Most attention is paidto the calculation of interpolation by Lagrange and Newton methods (right and left differences), software is developed and tested according to the appropriate algorithms and the interpolation is calculated and the error is calculated. Keywords: interpolation, Lagrange method, Newton`s method. ЗМІСТ ВСТУП 6 1 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ 7 1.1Інтерполяційний багаточлен Лагранжа 8 1.2Інтерполяційний поліном Ньютона 11 1.3Поняття похибки 13 2АЛГОРИТМИ МЕТОДІВ 16 3 РОЗРОБКА ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ 19 3.1 Вибір мови програмування 19 3.2 Вхідні та вихідні дані 19 3.3 Структура програмного забезпечення 20 Схема програми показана в додатку А 20 3.4 Інструкція користувача 20 4 ТЕСТУВАННЯ ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ 21 Дана таблиця експерементальних даних: 21 Виділяємо праву частину полінома, вибираємо команду меню Symbolics – Simplify, в результаті чого отримуємо : 21 Значення функції в заданій точці x=2.5 дорівнює: 21 Другий спосіб: 22 Визначаємо степінь полінома Лагранжа: 22 Будуємо поліном Лагранжа: 22 Визначаємо значення функції в точці 22 5 АНАЛІЗ ОТРИМАНИХ РЕЗУЛЬТАТІВ 24 Проведемо запуск створеної програми для визначення інтерполяції напруги методом Лагранжа та Ньютона (праві та ліві різниці) 24 Вводимо кількість значень x або y 24 Вводимо значення X[1],X[n] 24 Вводимо значення Y[1],Y[n] 24 Вводимо значення напруги 24 Обираємо один із трьох методів 24 Отримуємо значення в точці 24 Результати програми показані в додатку Б 24 ВИСНОВКИ 25 В даній курсовій роботі реалізована задача “Знаходження інтерполяційного многочлена Лагранжа”. Здійснено математичний опис задачі, постановку задачі та розробку програмного пакету згідно з постановкою. Розроблено алгоритм поставленої задачі. Складено і налагоджено програму на мові C#. 25 У процесі налагодження було одержано працездатний пакет програм. Роботу пакету перевірено на контрольному прикладі, одержано результати, що співпадають з теоретичними. 25 Результат розробки оформлений у вигляді програмного проекту, що приводиться у додатку до курсової роботи. 25 Подальший розвиток роботи можливий у бік поліпшення зовнішньогоінтерфейсу й адаптації програми до ширшого використання. 25 Додатки 27 Додаток А 28 Схема програми 28 Додаток Б 29 Результати роботи програми 29 Додаток В 32 Лістинг програми 32 ВСТУПСучасний час характерний різким розширенням розділів математики, багато в чому зв’язаним з створенням і розвитком засобів обчислювальної техніки. Проте можна сказати ще одне - числові машини можна використовувати ефективно лише за умови глибокого знання чисельних методів математики. Математичне моделювання-засіб дослідження реальних об’єктів та явищ використаних у геофізиці, хімії, геології, біології, медицині, психології, лінгвістиці та ін. науках. Математичне моделювання можна розглядати як засіб вивчення реальної системи шляхом заміни її більш зручною для експерементального дослідження системи (моделлю), яка зберігає суттєві риси оригіналу. Математичне моделювання включає такі етапи: дослідження об’єкта і створення його математичного опису; побудова алгоритму, який моделює поведінку об’єкта; перевірка адекватності моделі і об’єкта; використання моделі. Ефективність математичного моделювання в більшості визначається ефективністю використовуваних для розрахунків моделей обчислювальних методів і алгоритмів. У більшості випадків підбір підходящих рівнянь ускладнюється тим, що експериментальні дані отримані приблизно і вміщують похибку експерименту та обчислювань. 1 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІУ курсовій роботі проведено дослідження методів інтерполяції. Багатьом із тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експерементальним шляхом чи методом випадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних. [1]. Інтерполяція – це відтворення (наближення) виду деякої функції 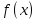 в точках в точках 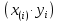 , , 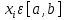 , , 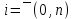 за допомогою функції наближення за допомогою функції наближення 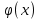 так, щоб виконувалася умова так, щоб виконувалася умова 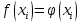 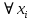 , , 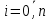 . (1.1) . (1.1)Найчастіше застосовується інтерполяція у вигляді полінома 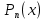 на проміжку [ на проміжку [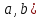 так, щоб значення цього полінома при заданих значеннях так, щоб значення цього полінома при заданих значеннях 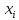 , які називаються вузлами інтерполяції, точно дорівнювало б заданим значенням функції , які називаються вузлами інтерполяції, точно дорівнювало б заданим значенням функції 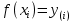 або цю умову можна записати так: або цю умову можна записати так: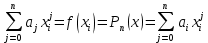 ; (1.2) ; (1.2)Інтерполяційний багаточлен однозначно визначається вузлами інтерполяції та значеннями функції в них. Так, якщо вони отримані шляхом експериментальних вимірювань, то вони мають похибку приладів, похибку методу експерименту, похибку випадкових впливів зовнішнього середовища. Оскільки багаточлен зберігає значення функції у вузлах інтерполяції, то йому притаманні і всі похибки значень точок інтерполяції, більш того, він може навіть посилювати так званий „шум” експерименту. Тому інтерполяція практично застосовується у тих випадках, де цими похибками можна знехтувати, наприклад, при роботі з таблицями та графіками (їхнє заміщення у розрахунках інтерполяційним поліномом). Інтерполяційний багаточлен ЛагранжаІнтерполяційний поліном Лагранжа 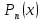 записують у вигляді: записують у вигляді: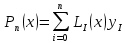 (1.3) (1.3)Де 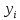 – значення функції у вузлах інтерполяції, а – значення функції у вузлах інтерполяції, а 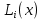 визначаються як: визначаються як: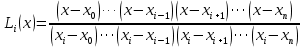 при при 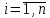 (1.4) (1.4)визначаються тільки вузлами інтерполяції і набувають в них значення: 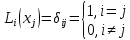 (1.5) (1.5)Формула Лагранжа дає простий вираз інтерполяційного багаточлена через задані значення функції i y і при фіксованих вузлах інтерполяції легко програмується. Для підбору степеня інтерполяційного полінома всі вузли можна зберігати у файлі та за необхідності вибирати потрібну їх кількість. Оскільки інтерполяційний багаточлен Лагранжа лінійно залежить від значень функції, то інтерполяційний багаточлен від суми 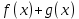 буде дорівнювати сумі інтерполяційних багаточленів буде дорівнювати сумі інтерполяційних багаточленів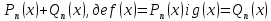 (1.6) (1.6)Для часткового випадку лінійної інтерполяції (наближення функції багаточленом 1-го степеня) за двома вузлами, формула Лагранжа буде мати вигляд: 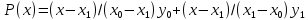 (1.7) (1.7) Похибку параболічної інтерполяції можна оцінити за допомогою залишкового члена ряду, який можна записати таким чином: 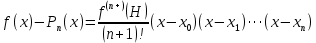 (1.8) (1.8)де точка ξ належить інтервалу, на якому розміщені вузли інтерполяції. Якщо на цьому інтервалі відоме найбільше значення 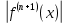 , яке будемо позначати , яке будемо позначати 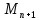 то оцінити похибку можна за такою формулою: 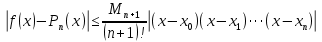 (1.9) (1.9)Похибку лінійної інтерполяції можна оцінити величиною: 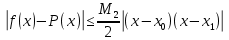 (1.10) (1.10)Де 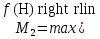 , , 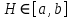 – інтервалу інтерполяції. – інтервалу інтерполяції.Для табличних функцій, аналітична форма яких невідома, застосувати такі оцінки досить важко і це обмежує практичне використання формули Лагранжа. Також до недоліків цієї формули можна віднести той факт, що результуючий степінь полінома буде відомим лише при розкритті всіх дужок і зведенні подібних, а, отже, формула не пристосована до нарощування вузлів інтерполяції (для збільшення степеня полінома необхідно виконати повний перерахунок усіх коефіцієнтів). Інтерполяційний поліном НьютонаНехай 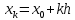 , де k – ціле число, , де k – ціле число, 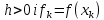 .Тоді величина: .Тоді величина: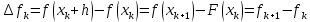 (1.11) (1.11)називається скінченною різницею першого порядку функції 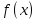 в точці в точці 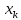 , вираз: , вираз: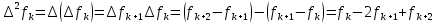 (1.12) (1.12)буде представляти скінченну різницю другого порядку. Скінченну різницю n-го порядку можна обчислювати за рекурентною формулою: 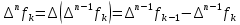 (1.13) (1.13)де n ≥ 1, 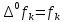 При обчисленні скінченних різниць, зручно записувати їх у таку таблицю: Таблиця 1.1 – Обчислення скінченних різниць
Якщо 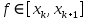 ,то існує така точка ξ ,то існує така точка ξ 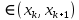 , що , що 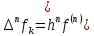 ξ) ξ)Скінченна різниця n-го порядку алгебраїчного багаточлена n-го степеня є постійною величиною (не залежить від k ), а скінченні різниці вищих порядків дорівнюють нулю. Часто у практичних задачах заздалегідь невідомий степінь полінома для отримання кращого наближення. Якщо в таких випадках застосовувати поліном Лагранжа, то це призведе до великої кількості обчислень. Краще застосувати такі поліноми, які дозволяють нарощувати степінь без виконання повного перерахунку. Таку властивість має інтерполяційний поліном Ньютона: 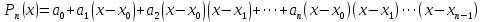 (1.14) (1.14) який отримується за допомогою рекурентного співвідношення: 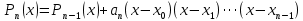 (1.15) (1.15)Інтерполяційний багаточлен Ньютона для будь-яких точок можна записати через розділені різниці: 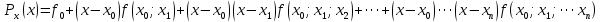 (1.16) (1.16)Поняття похибкиОсновними джерелами виникнення похибок обробки даних, отриманих різними шляхами (з експериментів чи у результаті розрахунків) є: наближеність початкових даних; похибка чисельних методів; похибка обчислень, комп‘ютерна похибка. Якщо чисельні методи застосовують для обробки даних, отриманих у результаті експериментів, то першим джерелом виникнення похибок будуть умови проведення іспитів, які певною мірою спотворюють дані. Так, похибки поділяють на систематичні та випадкові. Систематичні похибки можуть виникати за рахунок неправильно відкаліброваних приладів або систематичних перешкод при проведенні експерименту та знятті показників. Систематичні похибки будуть призводити до систематичних невірних результатів, а, отже, і невірних висновків на їхній основі. Тому необхідно дотримуватись умов проведення „чистих експериментів” і уникати виникнення систематичних похибок. Випадкові похибки обумовлені випадковими факторами, наприклад, впливом зовнішнього середовища, неточністю зняття показників приладів, неуважністю дослідника. Випадкові похибки можуть спотворювати точне значення як з надлишком, так і з недостачею, тому загалом вони будуть компенсуватись і прямувати до точного значення. Очевидно, що негативні наслідки від випадкових похибок значно менші, ніж від систематичних. У випадку, коли проводиться чисельний експеримент над математичною моделлю, отримані дані містять похибку, обумовлену наближеністю самої моделі до реального явища, яке вона описує. На основі отриманих даних формалізується задача, яку необхідно розв‘язати. Практичні задачі часто мають досить складний вираз і їх неможна розв‘язати аналітично. Тоді до задач застосовують чисельні методі. Більшість чисельних методів базується на спрощенні початкових складних функцій, що також призводить до виникнення похибки методу. Для спрощення реалізації методів, вони виражаються рекурентними формулами. На кожному кроці обчислень виконується операція округлення і в процесі багаторазового повторення рекурентної формули накопичується похибка обчислень. Необхідно пам‘ятати, що всі розрахунки за допомогою комп‘ютера виконуються над наближеними числами, які в процесі виконання дій округляються до порядку, що визначається точністю вибраного типу даних. Наприклад, у мові С/С++ тип float визначає дійсні числа, для представлення яких виділяється чотири байти, і точність представлення числа не перевищує шостого знака. Тип double – виділяє для запису дійсного числа вісім байтів і дає змогу зберігати більшу кількість значущих цифр дійсного числа (10-12 цифр). Щоб отримати результат із заданою точністю необхідно правильно вибирати тип даних (тип, який має точність на декілька порядків більшу, ніж задана) і враховувати, що чим більше число операцій над числами виконується, тим більшою буде накопичена похибка. Перед виконанням математичної обробки даних, їх необхідно підготувати. Перевіряти та переглядати дані зручніше, якщо вони впорядковані. Тому, першим кроком у підготовці даних є їхнє сортування. Якщо на основі експериментальних даних буде будуватись математична модель у вигляді деяких функцій вигляду 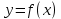 , або буде проводитись дослідження моделі, яка описується функцією, то дані мають бути відсортовані в порядку зростання значень аргументу цих функцій , або буде проводитись дослідження моделі, яка описується функцією, то дані мають бути відсортовані в порядку зростання значень аргументу цих функцій 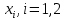 ,..., n, де n – кількість даних або це число ще називають об‘ємом вибірки. Наступним кроком у підготовці є перевірка їх на коректність. Для перевірки правильності даних існують спеціально розроблені методи, в основі яких лежить теорія математичної статистики. Але, навіть без застосування спеціальних теорій, дані можна перевірити на правильність просто їх візуальним переглядом. ,..., n, де n – кількість даних або це число ще називають об‘ємом вибірки. Наступним кроком у підготовці є перевірка їх на коректність. Для перевірки правильності даних існують спеціально розроблені методи, в основі яких лежить теорія математичної статистики. Але, навіть без застосування спеціальних теорій, дані можна перевірити на правильність просто їх візуальним переглядом. Точність наближеного обчислення залежить не від кількості значущих цифр, а від кількості вірних значущих цифр. Якщо число містить надлишкову кількість невірних значущих цифр, то його округлюють. При виконанні допоміжних обчислень кількість значущих цифр має братись на 1-2 розряди більше ніж задана точність. Якщо наближене число a > 0 має n вірних десяткових знаків, то відносна похибка обчислюється як 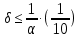 де α – перша значуща цифра числа a . де α – перша значуща цифра числа a . Абсолютна похибка алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних похибок цих чисел. Нехай 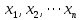 наближені числа, і наближені числа, і 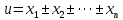 – їхня сума, то абсолютна похибка суми – їхня сума, то абсолютна похибка суми 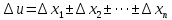 і сума абсолютних похибок і сума абсолютних похибок 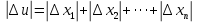 . В якості граничної абсолютної похибки суми можна взяти суму граничних похибок доданків. . В якості граничної абсолютної похибки суми можна взяти суму граничних похибок доданків.Абсолютну похибку неперервної функції 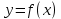 , що обумовлена достатньо малою похибкою аргументу , що обумовлена достатньо малою похибкою аргументу 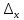 можна оцінити величиною: можна оцінити величиною: 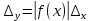 (1.17) (1.17)АЛГОРИТМИ МЕТОДІВАлгоритми методів Ньютона, та Лагранжа на рис. 2.1; 2.2 та 2.3 відповідно. 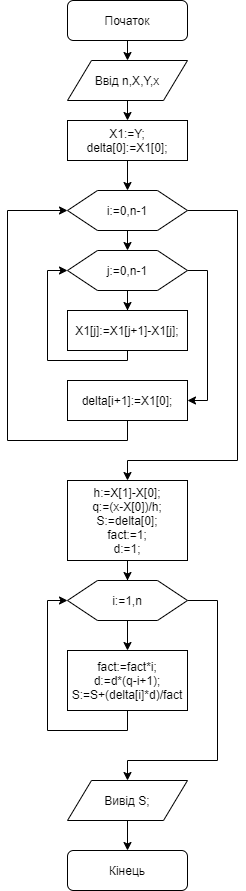 Рисунок 2.1 – Метод Ньютона (перша інтерполяційна формула) 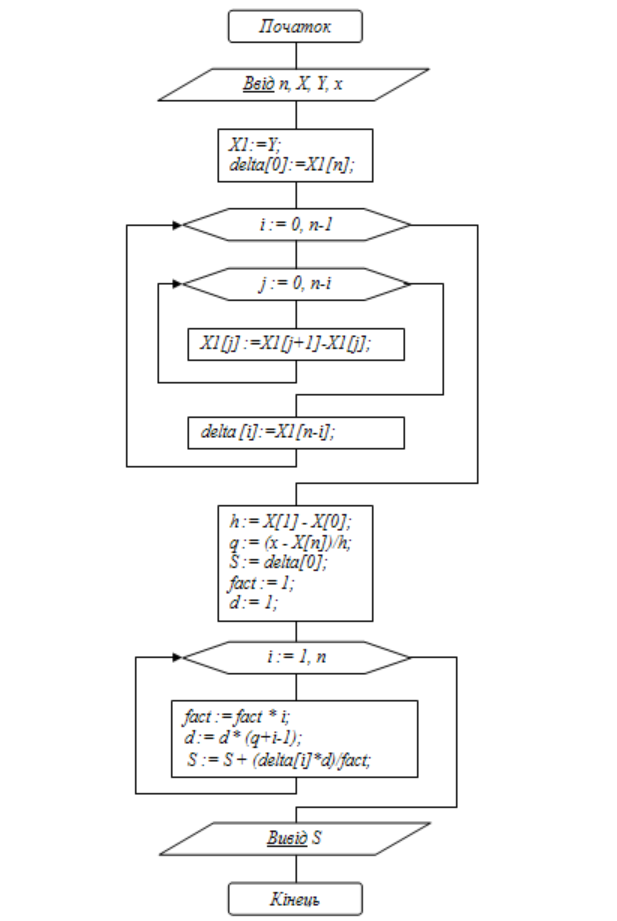 Рисунок 2.2 – Метод Ньютона (друга інтерполяційна формула) 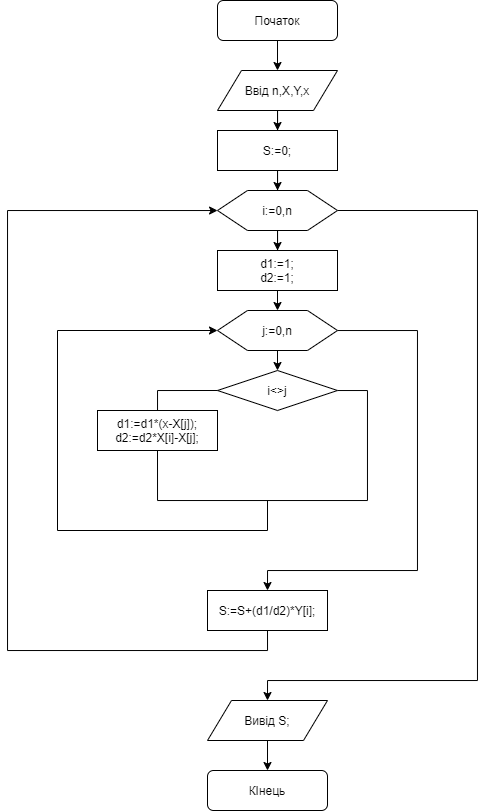 Рисунок 2.3 – Метод Лагранжа 3 РОЗРОБКА ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ3.1 Вибір мови програмуванняДля розробки заданого програмного забезпечення виберемо мову C# C# - об'єктно-орієнтована мова програмування з безпечною системою типізації для платформи .NET. Розроблена Андерсом Гейлсбергом, Скотом Вілтамутом та Пітером Гольде під егідою Microsoft Research (при фірмі Microsoft) Синтаксис C# близький до С++ і Java. Мова має строгу статичну типізацію, підтримує поліморфізм, перевантаження операторів, вказівники на функції-члени класів, атрибути, події, властивості, винятки, коментарі у форматі XML. Перейнявши багато що від своїх попередників мов С++, Delphi, Модула і Smalltalk С#, спираючись на практику їхнього використання, виключає деякі моделі, що зарекомендували себе як проблематичні при розробці програмних систем, наприклад множинне спадкування класів (на відміну від C++). 3.2 Вхідні та вихідні даніВхідні дані: тарировочна таблиця: Таблиця 3.1- тарировочна таблиця
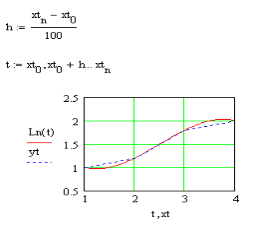
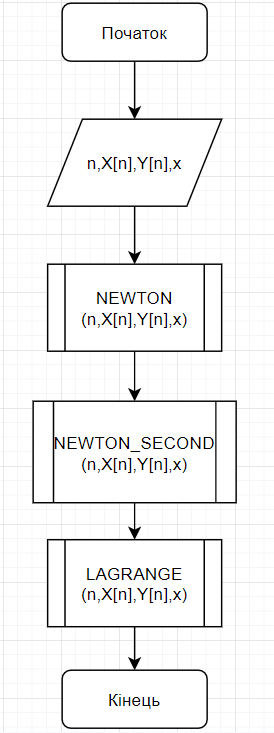
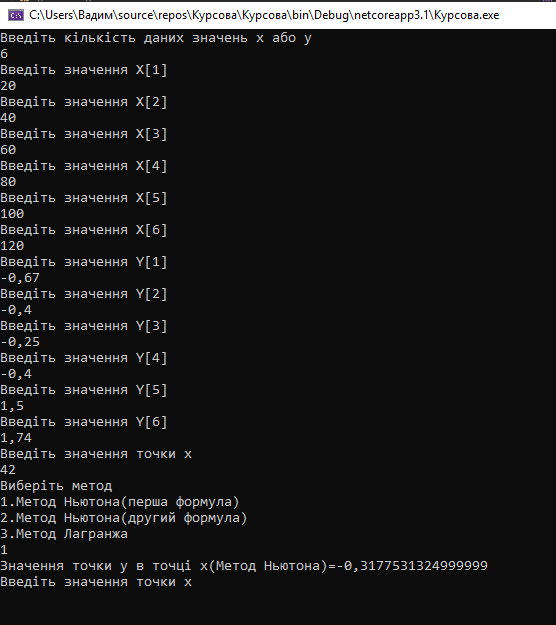
-початкові значення 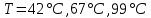 Вихідні дані: результат обчислення інтерполяції 3.3 Структура програмного забезпеченняПрограмне забезпечення складається з класу Program в якому міститься три методи обчислення задач інтерполяції: NEWTON() – обчислює праву різницю першого порядку NEWTON_SECOND() – обчислює ліву різницю другого порядку LAGRANGE() – обчислює метод Лагранжа Після визначення кількості даних, вводимо значення температури та напруги, після цього вибираємо метод який нам потрібен. Схема програми показана в додатку А 3.4 Інструкція користувачаПрограма, для вирішення інтерполяції , вимагає лише запуску та вибору кроку.Інші дані, які необхідні для роботи програми, потрібно ввести вручну, такі як температуру та напругу. Для розв’язання вводиться точка х (метод Ньютона(перша, друга форма)), та (метод Лагранжа), передбачає наступну точку за вже отриманими даними, закінчення програми. 4 ТЕСТУВАННЯ ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯДана таблиця експерементальних даних: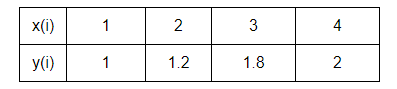 Таблиця 4.1 – експерементальні дані Таблиця 4.1 – експерементальні даніВизначити значення функції в заданій точці x=2.5 використовуючи інтерполяційний поліном Лагранжа. Побудувати інтерполяційний поліном Лагранжа. Перевірити вірність побудови полінома. Побудувати графіки інтерполяційного полінома Лагранжа та таблично заданої функції. Будуємо інтерполяційний поліном Лагранжа за табличними даними: 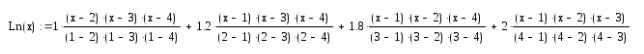 |

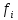
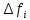
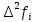
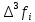
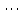
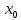
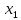
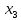
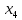
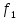
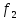
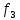
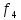
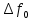
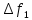
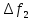
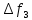
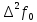
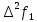
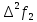
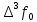
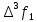
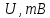
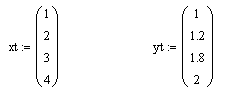
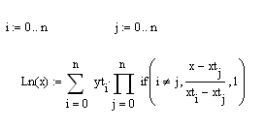
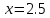
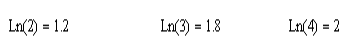
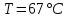 (Трьома методами)
(Трьома методами)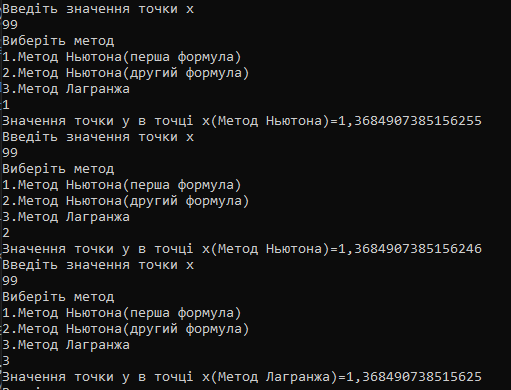
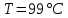 (Трьома методами)
(Трьома методами)