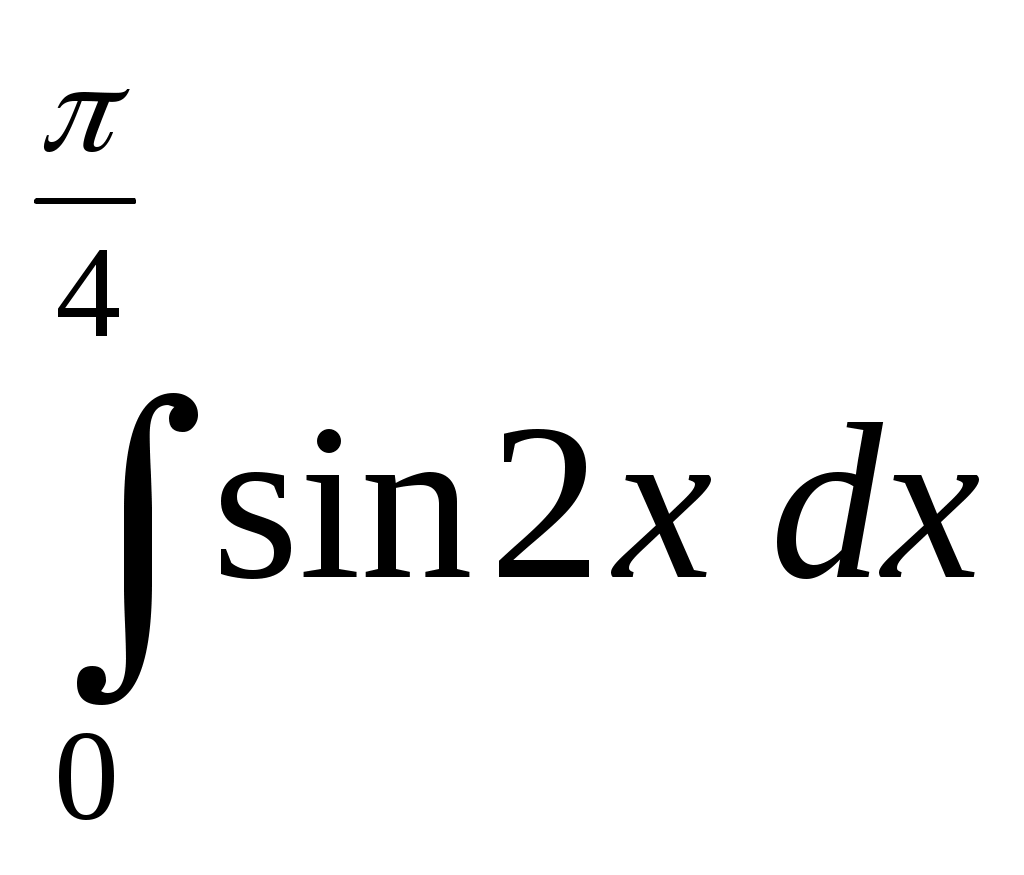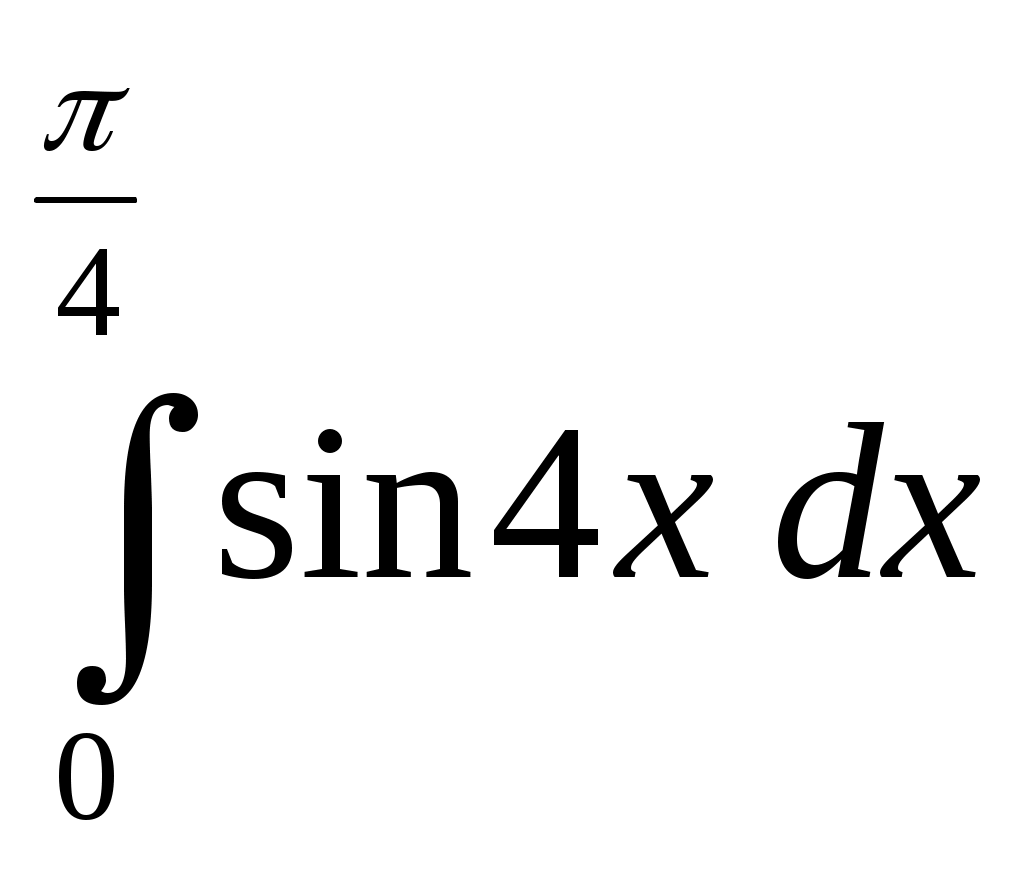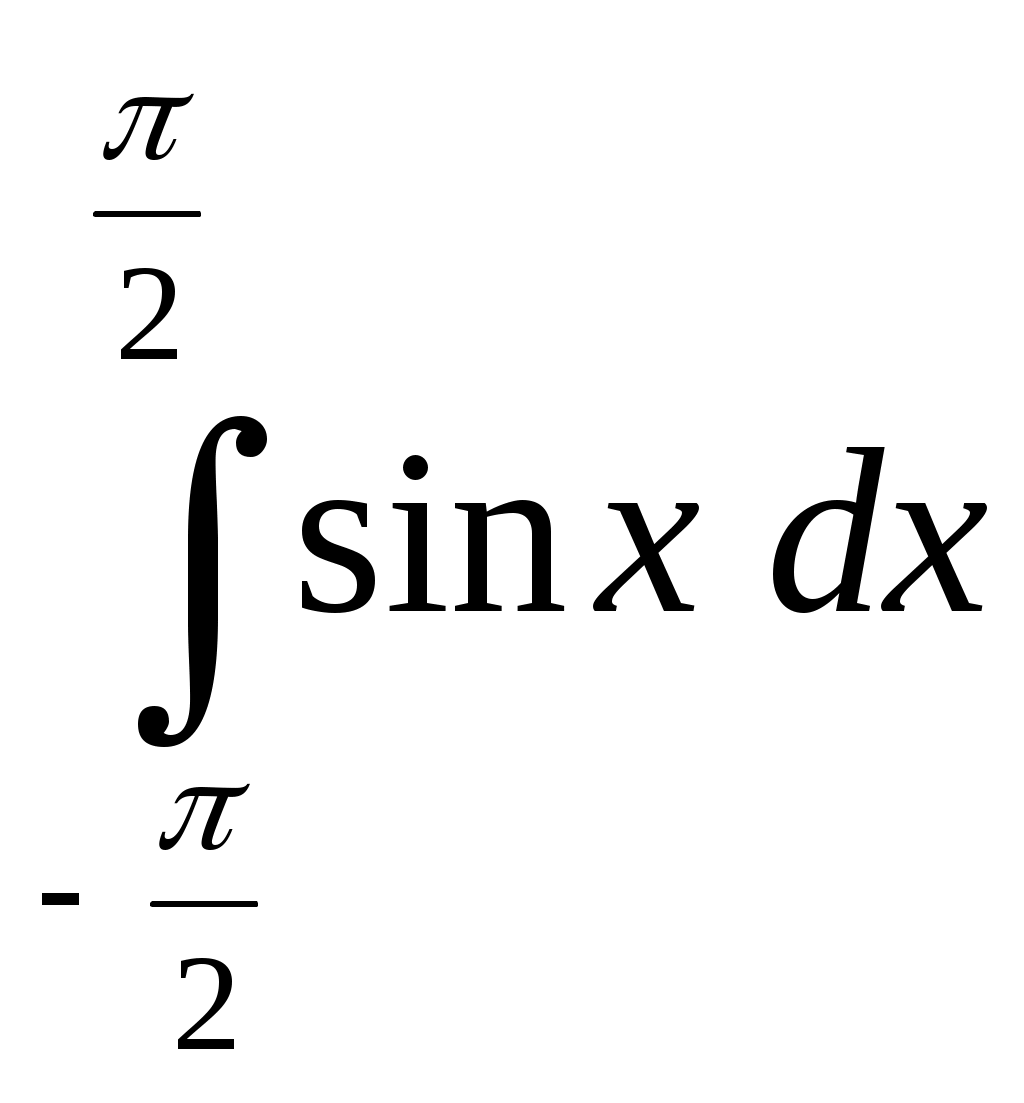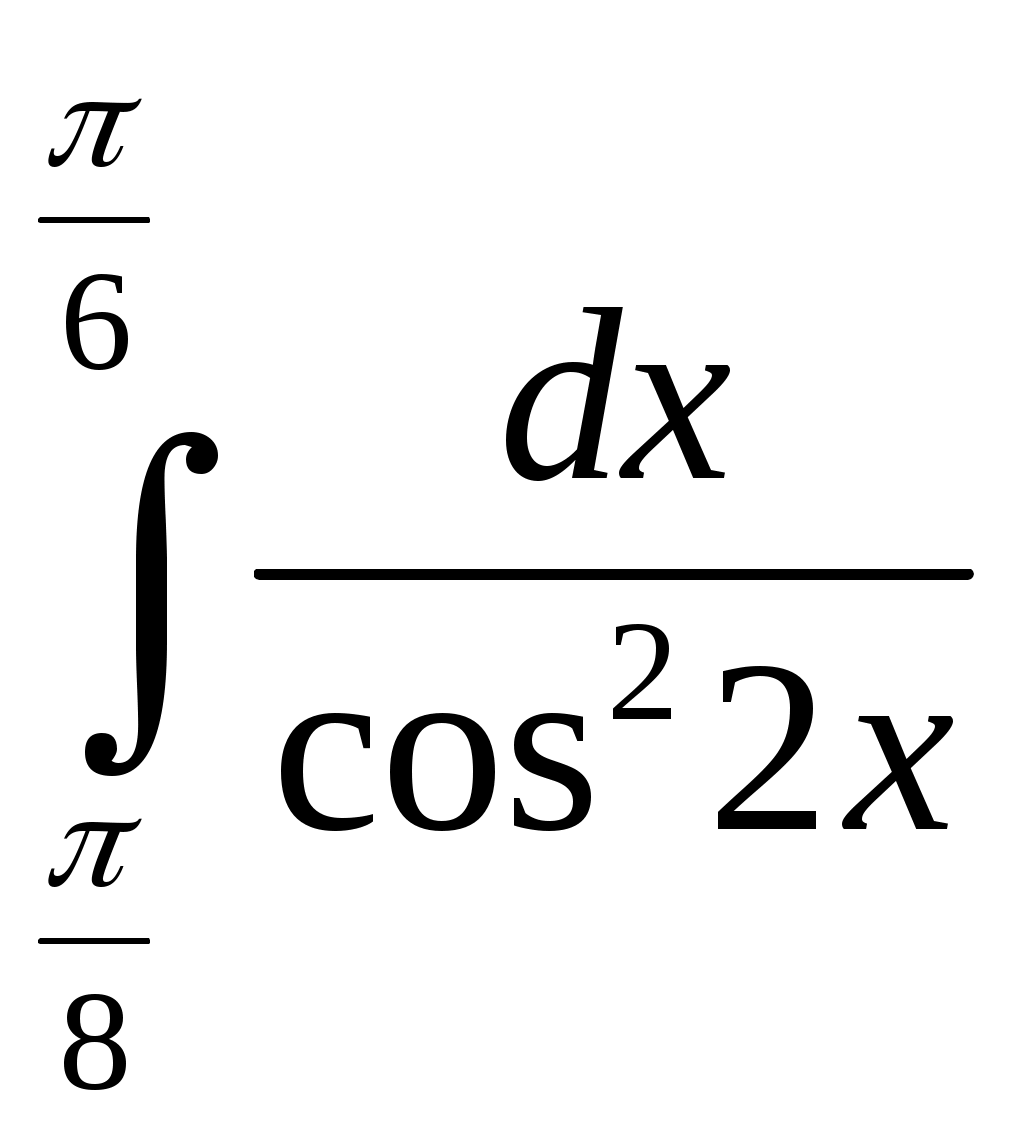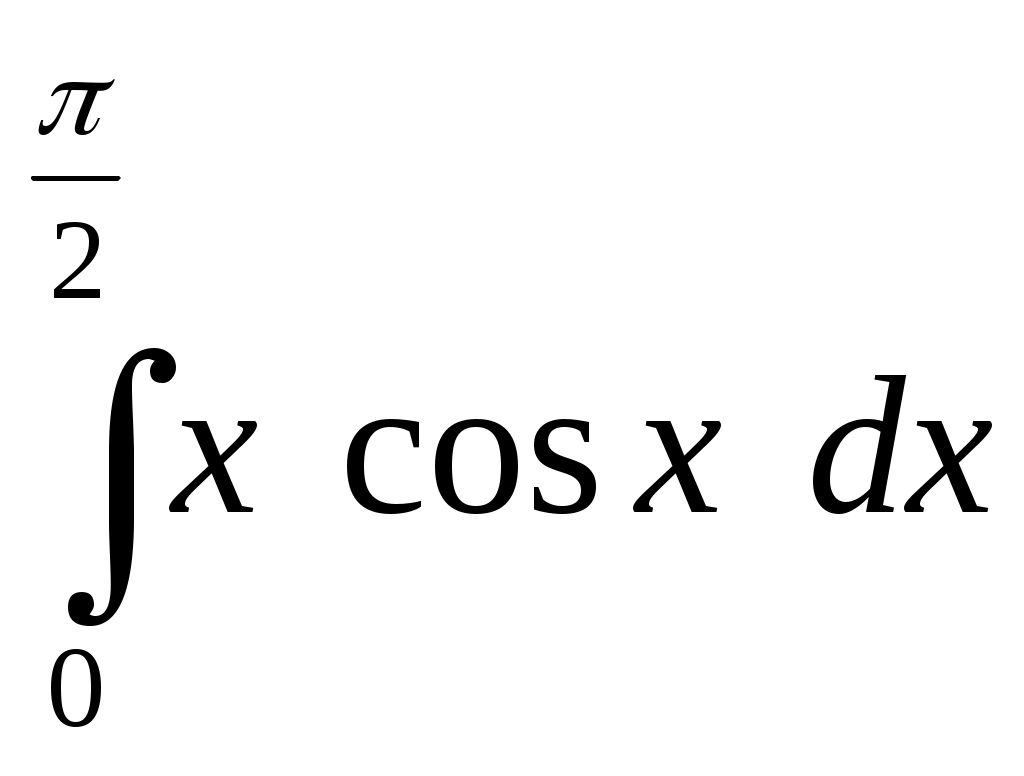Тест с ответами. Друзья, этот файл поможет вам сдать на хороший результат, однако не стоит жадничать сделайте специально пару ошибок Если нужна будет помощь в прохождении других тестов пишите в личные сообщения в матрицах жирным отмечены элементы, по которым искать ответ!
 Скачать 1.18 Mb.
|
|
Дифференциал функции y = x3 при x = 1 и x = 0,1 равен … 0,3 Достаточными условиями существования производной непрерывной функции в точке являются: существование и равенство двух односторонних пределов Если = 3, то бесконечно малая по сравнению с бесконечно малой … одного порядка Если = 3, то бесконечно малая по сравнению с бесконечно малой … третьего порядка (верно в другой формулировке) Заменив приращение функции дифференциалом, приближенно найти sin31°. 0,515 Заменив приращение функции дифференциалом, приближенно найти arctg 1,05. 0,81 Значение функции  при x → ∞ равно …1/3 Значение функции y = e-x при x → + ∞ равно … равно 0 Из непрерывности функции еще не следует ее дифференцируемость Интеграл … равен …
Интервалы вогнутости функции  можно найти как … Интервалы выпуклости функции y = x3/3 – 3x2 + 5x + 1 можно найти как … (– ∞; 3) Интервалы монотонного возрастания функции … равны …
Интервалы монотонного убывания функции … равны …
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
