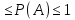Функция. Способы задания функции. Область определения и область изменения функции
 Скачать 83.03 Kb. Скачать 83.03 Kb.
|
Функция – это соответствие между двумя множествами Х и У, при котором каждому элементу множества Х найдется единственный элемент множества У. Способы задания функции:
Область определения функции – это множество значений переменной Х, при которых функция принимает действительные значения (обозначается D(f)). Область изменения функции – это множество значений, которые принимает сама функция (обозначается E(f)).
Предел функции в заданной точке - это такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. lim f(x) = a 1 Теорема: Предел суммы есть сумма пределов. lim (f(x) + u(x)) = lim f(x) + lim u(x) 2 Теорема: Предел произведения есть произведение пределов. lim f(x)*u(x) = lim f(x) * lim u(x) 3 Теорема: Предел частного есть частное пределов (если знаменатель не обращается в 0). 4 Теорема: Предел функции равен функции в предельной точке аргумента. lim f(x) = f (limx) Односторонние пределы функции: Это предел числовой функции , подразумевающий "приближения" к предельной точке с одной стороны. Чтобы функция имела предел необходимо существование односторонних пределов, они должны быть равны и конечны.
lim f(x) = f (x0) при х->x0
lim (дельта)y = 0 (дельта)y = y*(x0+(дельта)x) – y(x0) – приращение функции (дельта)х – приращение аргумента
f (x0-0) = f (x0+0) = f (x0) < бесконечность - условия непрерывности функции в точке Классификация разрывов функции: Точка разрыва функции – это точка Х0, в которой нарушаются условия непрерывности функции (3).
Точка Х0 называется точкой неустранимого разрыва I рода, если существуют односторонние пределы функции, они конечны, но не равным между собой. f (x0-0) НЕ равно f (x0+0) < бесконечность б = | f (x0-0) – f (x0+0) | - скачок 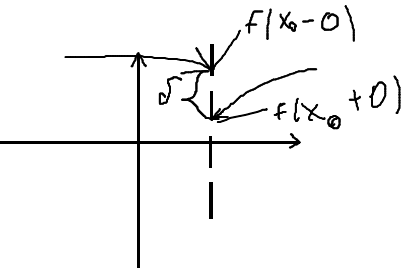
Точка Х0 называется точкой устранимого разрыва I рода, если существуют конечные, односторонние пределы функции, они равны между собой, но не равны значения функции в этой точке. f (x0-0) = f (x0+0) НЕ равно f (x0) Замечание: устранимый разрыв 1 рода можно искусственно устранить. Для этого надо значение функции f(X0) прировнять к значению. f (x0) = f (x0+0) 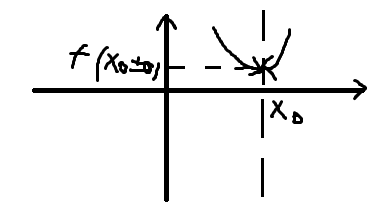
Точка X0 называется точкой разрыва II рода, если хотя бы 1 из односторонних пределов функции или оба не существуют или равны бесконечности.  f (x0-0) = бесконечность f (x0-0) = бесконечность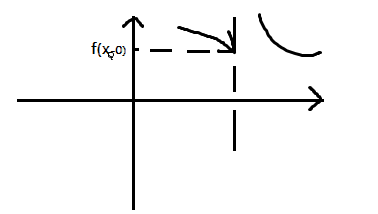 f (x0+0) = бесконечность f (x0+0) = бесконечность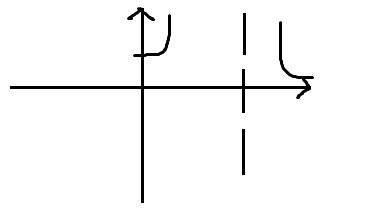 f (x0+0) = бесконечность f (x0+0) = бесконечность
Правила:
lim 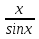 = (0\0) = 1 x->0 = (0\0) = 1 x->0lim 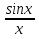 = (0\0) = 1 x->0 = (0\0) = 1 x->0
lim (1+X)^ 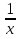 = (1∞) = e x->0 = (1∞) = e x->0lim (1+ 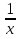 )x = (1∞) = e x->∞ )x = (1∞) = e x->∞
Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю произвольным образом. y| = 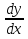 = lim = lim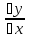 = lim = lim 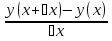 ⧍x->0 ⧍x->0Задача Ньютона: Найти скорость неравномерного прямолинейного движения точки в каждый момент времени t. Решение:
Vср= 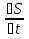
Vмгн = lim 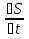 = lim = lim 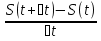 = S| (t) = = S| (t) = 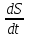 = S (t) ⧍t->0 = S (t) ⧍t->0
Механический смысл:
v(t) = 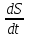 = S| (t) = S| (t)
a = 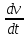 = S|| (t) = S|| (t)
I (t) = 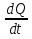 = Q| (t) = Q| (t)Геометрический смысл производной: y| = 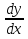 = lim = lim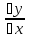 = lim = lim 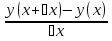 ⧍x->0 ⧍x->0
Уравнение нормали: y-y0 = (1\y| (x0)) *(x-x0) Уравнение касательной: y-y0 = y|(x0)(x-x0)
(u(v))| = u|(v)*v| Сначала находим производную внешней функции u|(v)
F (x;y) = 0 yx| - ?
x|=1; y|=y|
x2 - y3 = Sin (x-y) 2x – 3y2*y| = Cos (x-y)(1-y|) 2x – 3y2*y| = Cos (x-y) – Cos (x-y)*y| Cos (x-y)*y| - 3y2*y| = Cos (x-y) – 2x y|*(Cos (x-y) – 3y2) = Cos (x-y) – 2x y| = 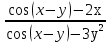
yx’ = yt’ \ xt’ yxx” = (yx’)t’ \ xt’
Дифференциал – это главная часть приращения функции. Линейная относительно ⧍Х и обозначается dy. dy = y'(x)*⧍x = y’(x)*dx - рабочая формула для вычисления дифференциала функции dx = x'(x)*⧍x = ⧍x Для того, чтобы найти дифференциал функции, надо производную функции умножить на дифференциал независимой переменной.
Если существует отношение 2-ух бесконечно малых или 2-ух бесконечно больших функций, то существует и предел их отношения, и он равен пределу отношений их производных, равен пределу отношения их вторых производных и т.д. (0\0; ∞\∞). lim 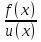 = lim = lim 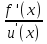 = lim = lim 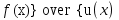
Производные: y” = (y’)’ y’’’ = (y”)’ y(n) = (y(n-1))’ Дифференциалы: dy = y’(x) dx dny = y(n)(x) dxn
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I. Экстремумы функции: Экстремум – это максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
График функции y=f(x) называется выпуклым на интервале, если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале , если он расположен выше любой своей касательной на этом интервале. Точка перегиба - это точка графика функции, в которой меняется направление выпуклости графика (выпуклый - вогнутый), а вторая производная меняет свой знак. Обычно находится следующим образом: 1) находим вторую производную 2) приравниваем ее к нулю и решаем уравнение. Полученные корни называются КРИТИЧЕСКИМИ ТОЧКАМИ ВТОРОГО РОДА 3) на оси Ох отмечаем эти точки и определяем знаки второй производной на каждом из полученных интервалов 4) как только при переходе через критическую точку вторая производная поменяла знак-вот Вам и точка перегиба...
Асимптота – это так называемая прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает ее, так что расстояние между ними делается бесконечно малой величиной. А) Вертикальная. х=а, где точка х=а является точкой разрыва 2-ого рода, т.е. lim f(x) = ∞; x->a+0 Б) Наклонная. y=kx+b k=lim 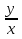 x->∞ x->∞b=lim (y-kx) x->∞ В) Горизонтальная. y=b b=lim f(x) x->∞
Если внешняя функция сложной функции возрастающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наибольшее значение. Если внешняя функция сложной функции убывающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наименьшее значение.
Функция F(x) называется первообразной для функции f(x), если F'(x)=f(x) Неопределенный интеграл – это совокупность всех первообразных для данной функции. ∫f(x) dx = F(x) + C Свойства неопределенного интеграла:
( ∫f(x) dx )’ = f(x)
d ( ∫f(x) dx ) = f(x) dx dy = y’(x) dx
∫ d (F(x)) = F(x) + C
∫ (f(x) + u(x)) dx = ∫ f(x) dx + ∫u(x) dx
∫ C*f(x) dx = C ∫ f(x) dx
∫ f(x) dx = ∫ f(u) du
Тождественное преобразование подинтегрального выражения и приведения его к табличному виду.
Если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций, то справедливы формулы: ∫ u dv = uv - ∫ v du
Заключается во введении новой переменной интегрирования. ∫ f(x) dx = ∫ f(u(t)) * u’(t) dt
Найти: Площадь криволинейной трапеции ограниченной линиями.
⧍Xi = Xi – Xi-1
Sпроизв = f (Si)*⧍Xi
S = lim
Определенный интеграл – это число, равное пределу N-ой интегральной суммы, когда наибольший из частичных отрезков разбиения стремится к нулю при N->∞. Определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x) и прямыми у=0; х=а; х=b. Свойства:
Справедливо для любого конечного числа разбиения числа A-B.
a∫b f(x) dx = F(b) – F(a) Правило. Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.
a∫b f(x) dx = t1∫t2 f(u(t)) * u’(t) dt
a∫b u dv = uva|b - a∫b v du
А) Четная. 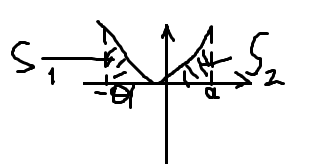 -a∫a f(x) dx = 2 0∫a f(x) dx Б) Нечетная. 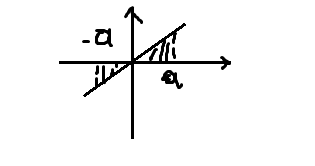 -a∫a f(x) fx = 0
Найти кривую, проходящую через начало координат tg угла наклона касательной и который равен удвоенной абсциссе Решение: Tgα = y’ = 2x y’ = 2x
y(0) = 0 - начальное условия y’ = 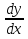 = 2x = 2xdy = 2x dx ∫ dy = ∫ 2x dx y = 2 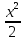 + C + Cy = x2 + C - общее решение
0 = 02 + C => C = 0 y = x2 - частное решение Диф. Уравнение – уравнение вида F (x, y, y'….y(n)), где F зависит от независимой переменной, функции этой переменной, ее производных и дифференциалов различных порядков. Порядок диф. Уравнения – это наивысший порядок производной, входящий в данное уравнение.
Y = u(x, C0) - частное решение
Ф (x, y, c) = 0 - общий интеграл
Ф (х, у, с) = 0 – частный интеграл Задача Коши: Нахождение частного решения диф. Уравнения F (x, y, c) = 0 удовлетворяющего начальному условию. y (x0) = y0
Диф. Уравнение с разделенными переменными – уравнение вида: f (x) dx + u (y) dy = 0 ∫ f(x) dx + ∫ u (y) dy = C F(x) + Ф(y) = C - общий интеграл
Диф. Уравнение с разделяющимися переменными – это уравнение вида: f1(x) * u1(y) dx + f2(x) * u2(y) dy = 0 Решение: Разделим переменные. 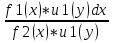 + + 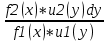 = 0 = 0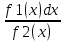 + + 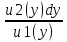 = 0 = 0
Линейные диф. Уравнения 2ого порядка с постоянными коэф. – это уравнение вида: a0*y” + a1*y’ + a2*y = f(x) f(x) 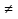 0 – неоднородное 0 – неоднородноеf(x) = 0 – однородное a0*k2 + a1*k + a2 = 0 - характерное уравнение Структура общего решения уравнения имеет вид: y = C1*y1 + C2*y2
Комбинаторика – это математическая наука, изучающая вопросы о том, сколько различных комбинаций, подчиненных тем или иным условием, можно составить.
Размещениями из N по M элементов называют такие соединения, в каждом из которых по M элементов и различаются такие соединения друг от друга только самими элементами и их порядками. Anm = n (n-m+1) 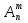 = = 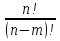
Перестановками из N элементов называются такие соединения, в каждом из которых по N элементов U отличаются такие соединения только порядком самих элементов. Pn = 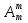 = = 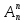 = = 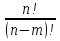 = n! = n!Pn = n!
Сочетаниями из N элементов по M называются такие соединения, в каждом из которых по M элементов и отличаются такие соединения только самими элементами. 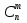 = = 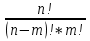 Свойство сочетания: 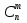 = = 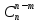
Виды событий:
Выстрел.
Осечка.
Попадание и промах.
Попадание при 1 выстреле, не исключает промах при 2 выстреле.
Попадание при 1 выстреле исключает промах при 1 выстреле.
Кубик кидают, 1 из 6.
Попадание и промах.
Как и в полной группе.
Вероятностью случайного события А называется отношение числа благоприятствующих исходов данного испытания к общему числу всех равновозможных несовместных исходов испытания образующих полную группу. P(A) = 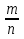 Свойства:
Статистическая вероятность случайного события А – это постоянное число, около которого группируются относительные частоты этого события, по мере увеличения числа испытаний.
Пусть на плоскости имеется некоторая область D с известной площадью SD. В этой области есть область d с площадью Sd. В область D наудачу бросается точка. Найти вероятность того, что точка попадет в область d. P(A) = 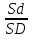 |