Моделирование поведения потребителей. Е. М. Крипак, О. Г. Габдуллина, Е. В. Бут
 Скачать 0.75 Mb.
|
2 Постановка задачиПредпочтения потребителя описываются функцией полезности  , доход равен I, а цены товаров p=( ). Полагая, что поведение потребителя рационально (то есть он выбирает такие количества каждого блага из товарного набора, которые позволяют ему максимально удовлетворить свои потребности при наличии ограниченного дохода) требуется:1) определить оптимальный набор товаров А, который выберет потребитель при фиксированном доходе и заданном векторе цен, а также достигнутый уровень полезности. Проиллюстрировать на графике взаимное расположение кривой безразличия и бюджетной прямой в оптимальной точке; 2) определить оптимальный набор товаров В, если цена второго блага повысилась на p2 денежных единиц, также компенсационное изменение дохода для сохранения прежнего уровня полезности и соответствующий потребительский набор С; 3) привести геометрическую интерпретацию пунктов 1 и 2: построить в пространстве товаров исходную бюджетную линию В0, бюджетную линию В1, после изменения цены 2 товара и В2 при наличии компенсации; построить кривые безразличия U0 и U1, соответствующие первому и второму оптимальному набору (В0 и B1); указать первый оптимальный набор потребителя А, второй оптимальный набор потребителя В (в случае изменения цены без компенсации), а также набор С, который является оптимальным в случае компенсационного изменения дохода. 4) построить аналитические функции спроса, как функции дохода и вектора цен; 5) провести анализ функций спроса, используя показатели эластичности по доходу и цене. Рассчитать действие эффекта замены, используя уравнение Слуцкого. Пример 0 варианта задания
3 Порядок выполнения работыПостроим математическую модель задачи потребительского выбора:    где n=2 – число потребляемых товаров или благ,  – потребительский набор,  функция полезности потребителя.Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача – задача потребительского выбора – является задачей нелинейного программирования. Рассмотрим возможности построения и исследования модели потребительского выбора с использованием ППП MathCad и «MS Excel». Применяя MathCad, откроем рабочий лист, определим целевую функцию и ограничения, зададим начальные условия и в решающем блоке под ключевым словом «Given» сформулируем задачу и применим функцию «Maximize», реализующую метод сопряженных градиентов. При использовании для расчетов ЭТ «MS Excel» применяется модуль «Поиск решения», предназначенный для решения задач нелинейного программирования. Для инициации процесса решения следует внимательно подойти к выбору начальных значений искомых переменных. В общем случае учитываются особенности требований применяемого метода и наличие априорной информации. Исследовав свойства рассматриваемой функции полезности, представленной функцией Стоуна, в данном случае в качестве начального приближения может быть взята любая точка из области допустимых решений, удовлетворяющая условию  Процесс решения представлен на рисунках 1 и 2. Анализируя результаты, можно сделать вывод, что потребитель выберет первое благо в количестве x1=97 единиц, второе благо в количестве х2=43 единицы, при этом полезность набора составит 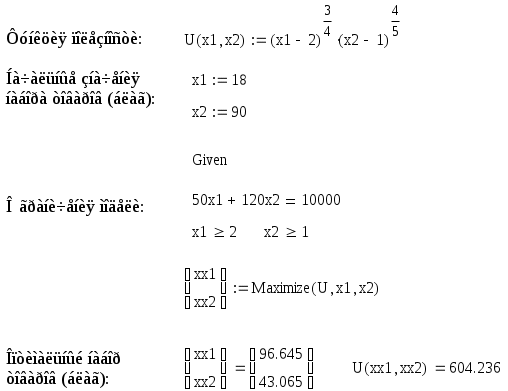 =600,23. Рисунок 1 – Решение задачи потребительского выбора в системе «MathCad» 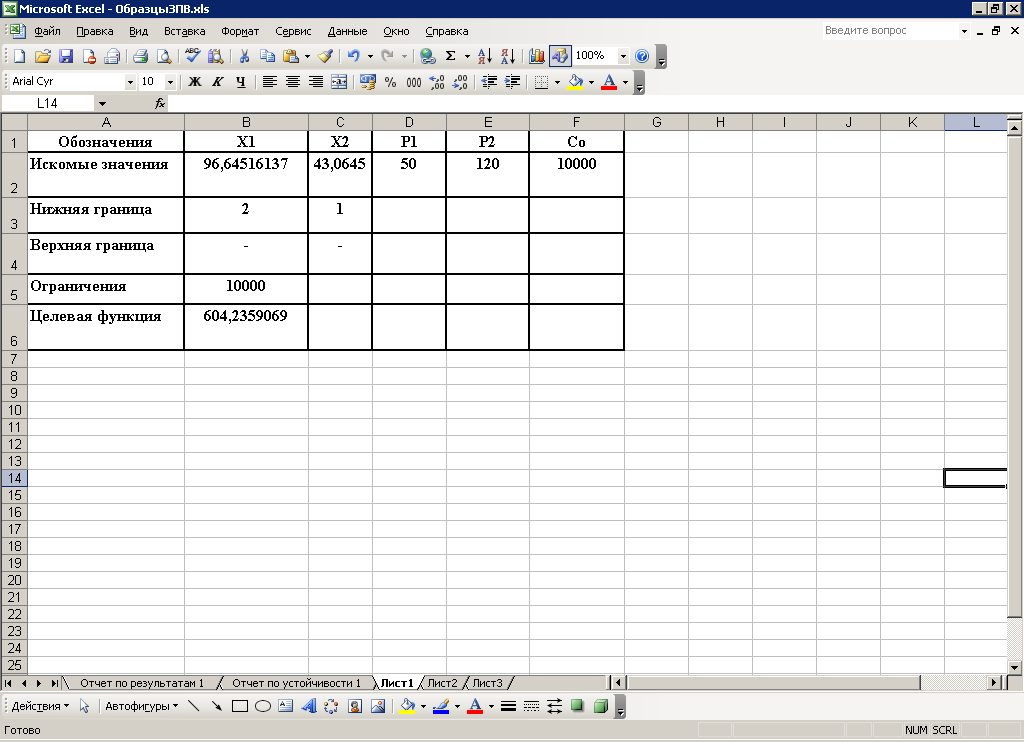 Рисунок 2 – Решение задачи потребительского выбора в ЭТ «MS Excel» На представленном ниже рисунке 3 изображено взаимное расположение кривой безразличия и бюджетной прямой в точке локального рыночного равновесия потребителя. 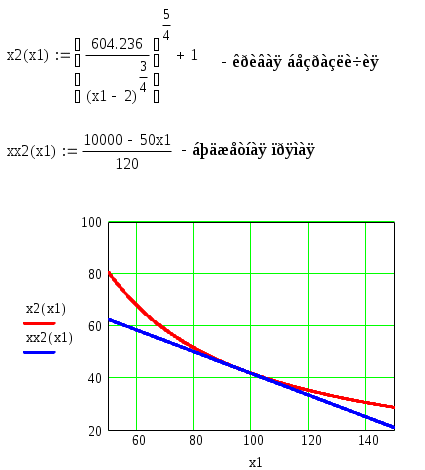 Рисунок 3 – Геометрическая интерпретация решения задачи потребительского выбора Предположим, что цена второго блага повысилась на 10 единиц и стала равна 130 единицам. Решение задачи представлено на рисунке 4. В этом случае оптимальным выбором будет набор В, в котором х1=97, х2=40, а полезность составляет 565,86 единиц. В результате уровень полезности будет снижен, для сохранения которого возможно предусмотреть компенсацию дохода. С любой задачей математического программирования связана двойственная с ней задача. В математической экономике исходят из того, что индивиды максимизируют свою полезность при заданном бюджетном ограничении. Это и есть исходная задача потребителя. Двойственной к ней задачей является задача минимизация расходов, которые необходимо сделать потребителю для того, чтобы достичь некоторого заданного уровня полезности. 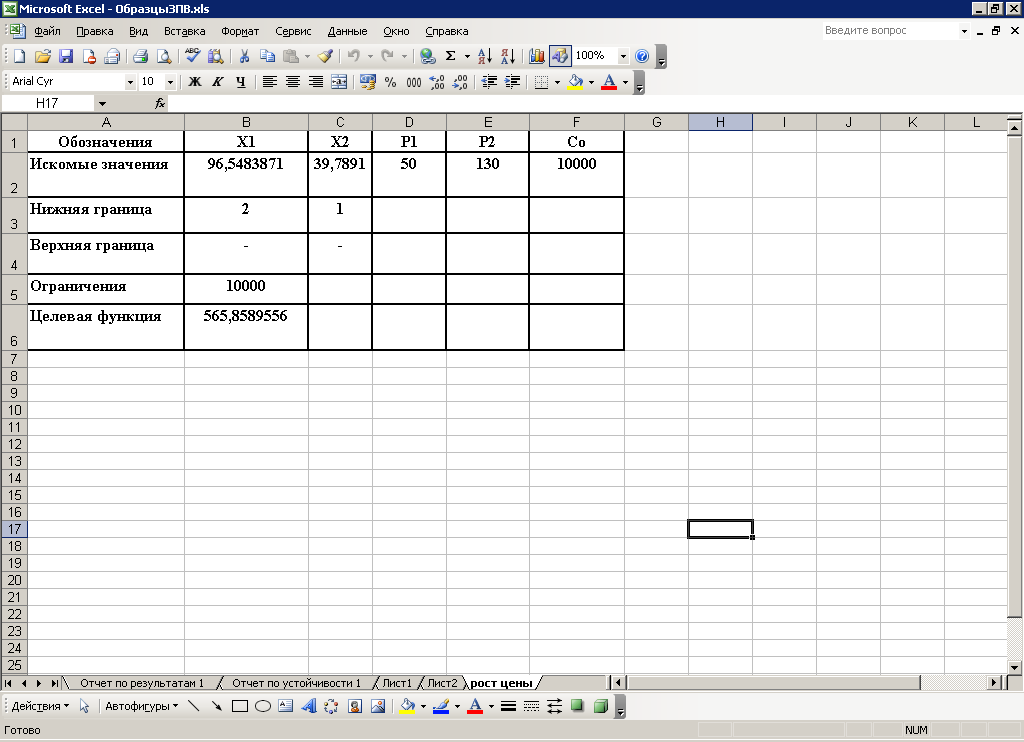 Рисунок 4 Решение задачи при увеличении цены второго товара в ППП ЭТ «MS Excel» Задача минимизации расходов при заданном уровне полезности  имеет следующий вид:   Таким образом, для определения величины компенсации следует решить двойственную задачу, которая для рассматриваемого примера будет иметь вид: 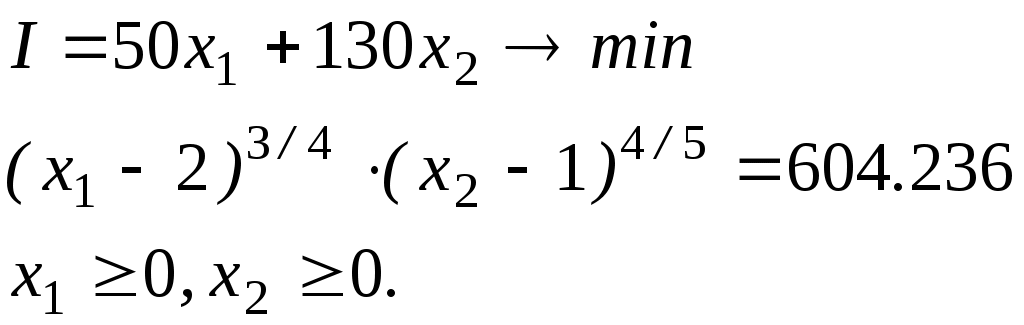 Решим полученную задачу оптимизации в ППП «Mathcad» и ЭТ «MS Excel», аналогично решению задачи потребительского выбора (рисунки 5 и 6). Таким образом, если цена 2 товара повысилась и стала равной 130 ед., то доход должен достичь величины 10422 ед. При этом потребление первого блага возрастет на 4 единицы, а потребление второго блага снизится на 2 единицы. 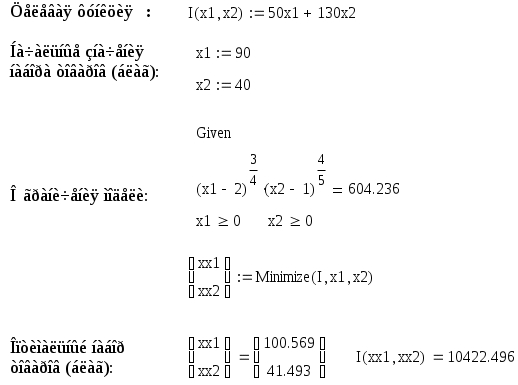 Рисунок 5 Решение двойственной задачи в ППП «Mathcad» 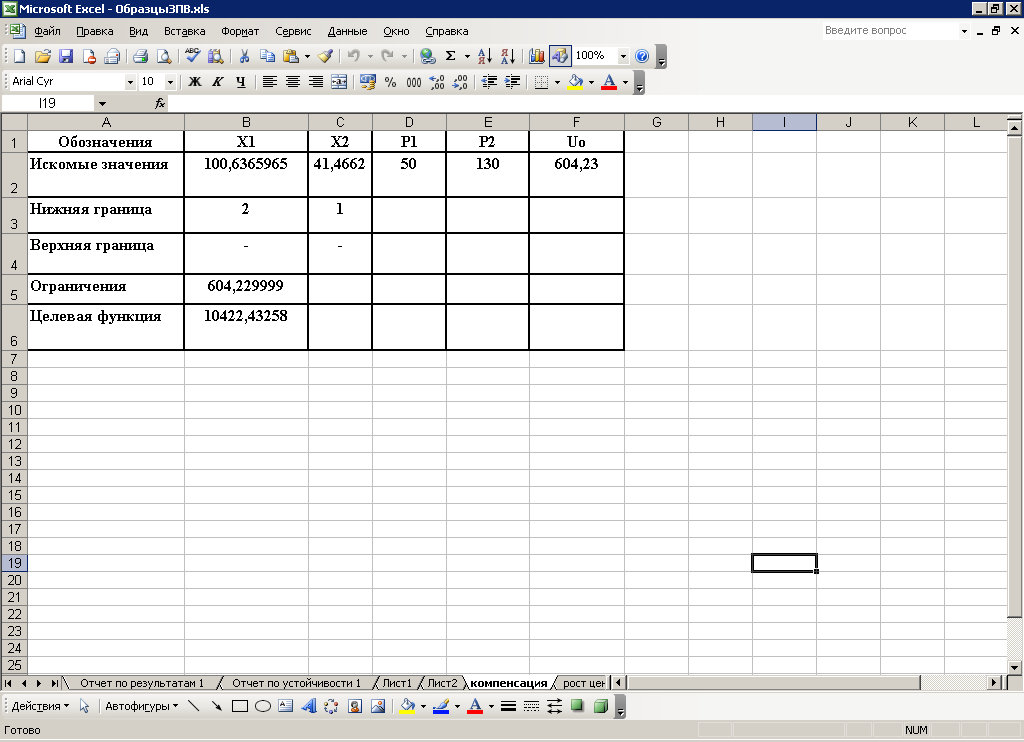 Рисунок 6 Решение двойственной задачи в ППП ЭТ «MS Excel» Графическая интерпретация решения представлена на рисунке 7. На рисунке 8 проиллюстрировано расположение бюджетных линий и кривых безразличия для трех, описанных выше случаев, а также указаны: первый оптимальный набор потребителя А, второй оптимальный набор потребителя В (в случае изменения цены без компенсации), набор С, который является оптимальным в случае компенсационного изменения дохода. 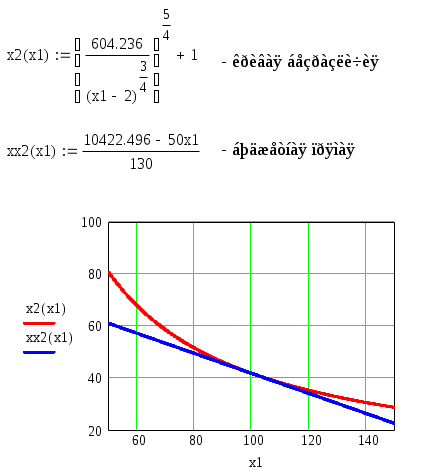 Рисунок 7 – Геометрическая интерпретация решения двойственной задачи 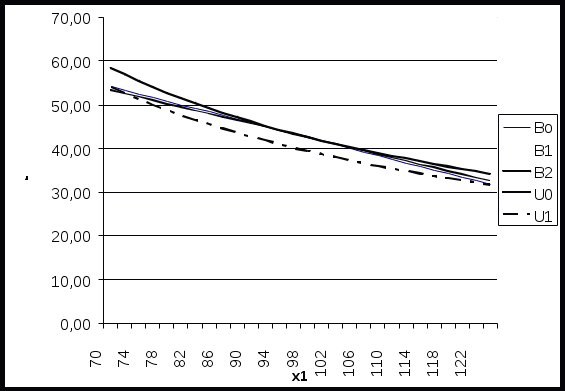 А В С  Рисунок 8 – Общая геометрическая интерпретация решения задачи потребительского выбора для трех случаев Перейдем к вопросу построения функции спроса. Оптимальный потребительский набор – точка локального рыночного равновесия потребителя – получен при фиксированных ценах и доходе, следовательно, при изменении дохода или цен изменится и оптимальный выбор потребителя. Множество координат решения задачи потребительского выбора есть функция дохода и цен, называемая функцией спроса: 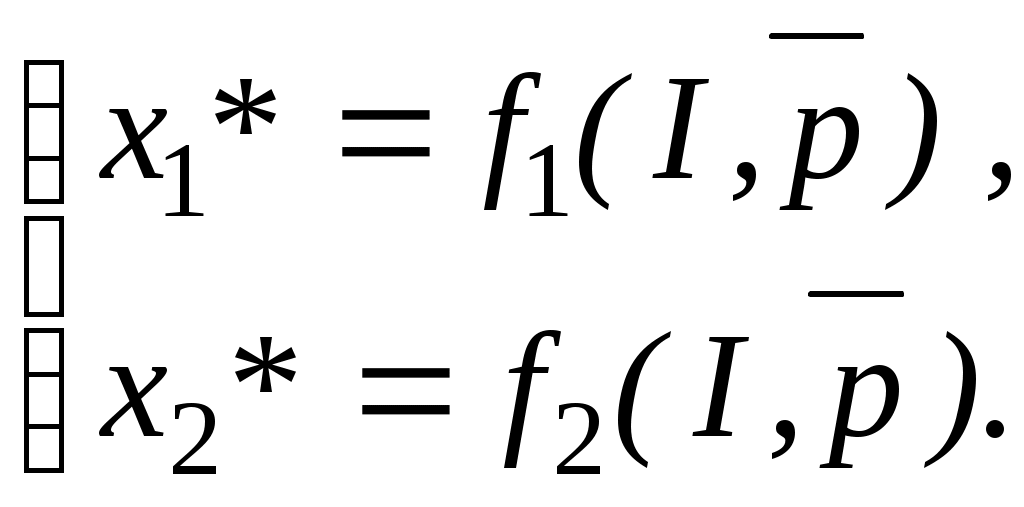 Таким образом, для табличного представления функции спроса найдем множество точек локального рыночного равновесия, полученных при решении задачи потребительского выбора в случае изменения дохода и цен в анализируемом диапазоне. Рассмотрим следующее изменение переменных:    Результаты решения соответствующих задач представлены в таблице 1. Таблица 1 – Спрос на товары при изменении дохода и цен
Продолжение таблицы 1.
На основе табличного представления будем строить аппроксимацию функции спроса как трехфакторную функцию дохода и цен. На начальном этапе аппроксимации функции спроса необходимо выбрать спецификацию функции. Эмпирические исследования показывают, что спрос на потребительские товары эффективно аппроксимируется степенными функциями дохода и цен. Будем строить функцию спроса на первый товар в следующем виде:  Для оценки параметров методом наименьших квадратов проведем предварительно линеаризацию данных путем логарифмирования обеих частей уравнения (таблица 2):  Таблица 2 – Результаты логарифмирования
Продолжение таблицы 2.
Для нахождения параметров  воспользуемся пакетом «MathCad». Сформируем матрицу X, вектор Y, и найдем параметры функции спроса, используя метод наименьших квадратов:  .Результаты расчетов параметров функции спроса на первый товар представлены на рисунке 9. 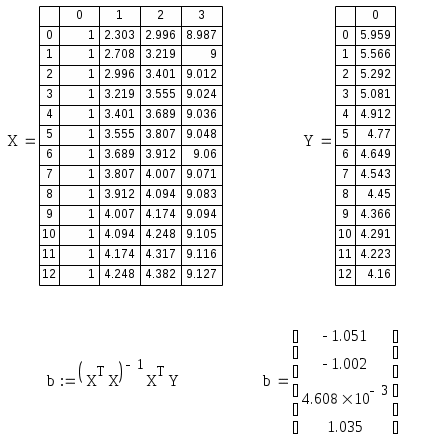 Рисунок 9 – Диалоговое окно нахождения параметров функции спроса на первый товар Таким образом, функция спроса на первый товар примет вид:  .Определим среднюю относительную погрешность аппроксимации по формуле: 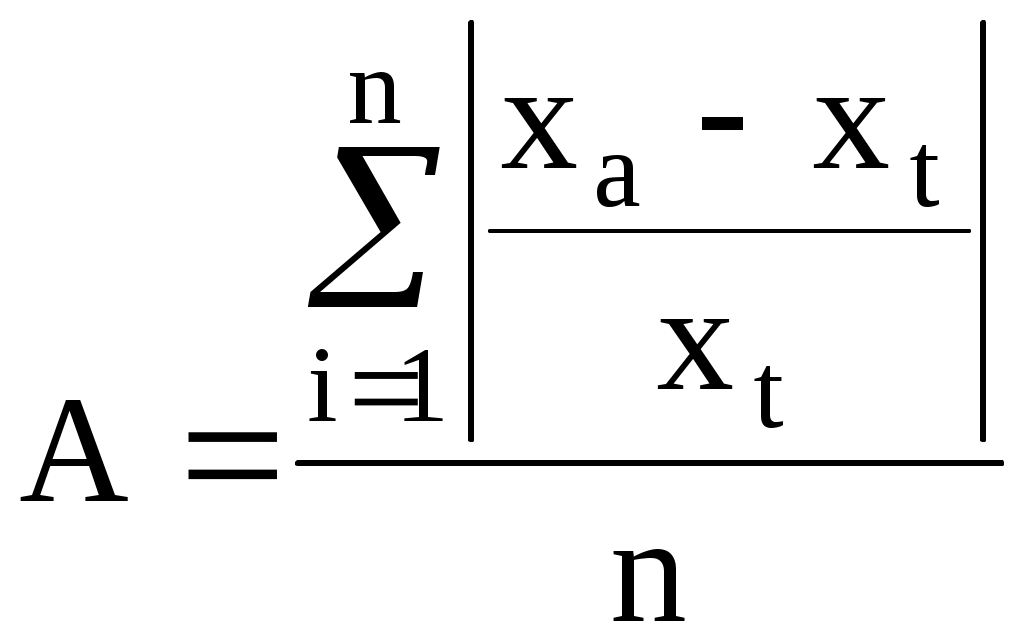 ,где xa – значения, рассчитанные с помощью построенной функции, xt –значения, заданные таблично. Средняя относительная погрешность аппроксимации для спроса на первый товар равна 0,0003687 %. Следовательно, построенная функция хорошо аппроксимирует исходные данные, и может использоваться для анализа значений результативного признака. Аналогичные действия проделаем и для второго товара (рисунок 10).  Рисунок 10 – Диалоговое окно нахождения параметров функции спроса на второй товар Функция спроса на второй товар имеет вид:  .Средняя относительная погрешность аппроксимации составила величину 0,0003375 %. Следовательно, построенная функция спроса на второй товар также хорошо аппроксимирует исходные данные, и может использоваться для анализа значений результативного признака. Замечание. В ряде случаев, например, если функция полезности является неоклассической, возможно аналитическое построение функции спроса. Для построения функции спроса запишем задачу потребительского выбора в общем виде:    Согласно теории полезности отношение предпочтения обладает свойствами сравнимости, транзитивности, рефлексивности, непрерывности, строгой выпуклости. Представляющая это отношение предпочтения функция полезности является непрерывной, возрастающей, строго квази-вогнутой и дифференцируемой во всех точках. Потребитель может потреблять только неотрицательные количества каждого блага. Кроме того, бюджетное множество является ограниченным, замкнутым, непустым и выпуклым, следовательно, предпосылка о строгой выпуклости отношения предпочтения позволяет переписать бюджетное ограничение - неравенство в виде равенства:  .Экономически это означает, что поскольку функция полезности является возрастающей, то потребитель максимизируя полезность, будет вынужден расходовать весь свой доход на покупку товаров и услуг. Для решения задачи (построения аналитических функций спроса) с ограничением в форме равенств запишем функцию Лагранжа:  .Необходимым условием максимума функции Лагранжа является равенство нулю ее частных производных по благам x1, x2 и неопределенному множителю . Найдя частные производные и приравнивая их к нулю, получим систему: 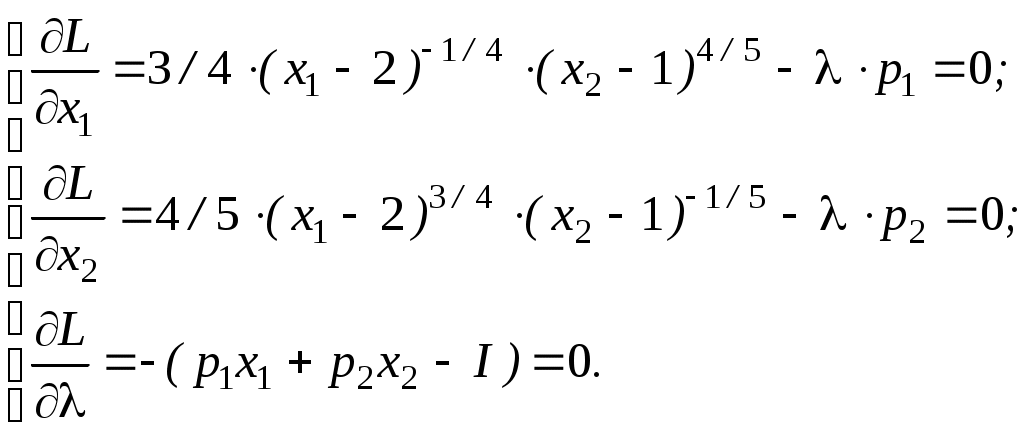 Решая систему относительно x1 и x2, получим следующие функции спроса:   .Для функции полезности Стоуна  денежные расходы на покупку каждого из благ, входящих в товарный набор, составляют постоянную долю от дохода, которая определяется предпочтениями потребителя в отношении этих благ. Так, на покупку первого блага потребитель всегда будет расходовать  часть своего дохода, а на покупку второго блага:  часть своего дохода, независимо от цен этих благ. Такого рода функции называются функциями некомпенсированного спроса потребителя. Их также называют функциями маршаллианского спроса в честь великого английского экономиста Альфреда Маршалла. Далее проведем анализ построенных функций. Исследуем влияние изменения дохода.  ;  , следовательно, товары являются ценными, и спрос на них возрастает по мере увеличения дохода. В этом случае определяют коэффициенты эластичности спроса по доходу, что позволит классифицировать товары. Эластичность спроса по доходу определяется по формуле:  . ;  =1,035. ;  =0,965.В оптимальной точке эластичность спросу по доходу на блага первого вида будет равна 1,035, на блага второго вида 0,965, что соответствует товарам со среднеэластичным спросом по доходу, или товарам второй необходимости. Это означает, что увеличение дохода на 1 % приведет к увеличению спроса также приблизительно на 1 %. Анализируя влияние изменения цены можно сделать вывод, что рассматриваемые товары относятся к группе традиционных, спрос на которые с ростом цены падает:  , Эластичность спроса по цене определяется по формуле:  .При i=j имеем прямую эластичность по цене, при ij перекрестную эластичность.     На основе изучения величин эластичностей по цене можно заключить, что оба товара являются среднеэластичными по цене и представляют необходимые блага. Так как все перекрестные коэффициенты эластичности положительны, но мало отличаются от нуля, то можно заключить, что блага х1 и х2 являются не конкурирующими благами. Рассчитаем действие эффекта замены, используя уравнение Слуцкого, которое позволяет отразить действие эффекта замены и эффекта дохода на результирующее изменение спроса. Уравнение имеет вид:  ,где первое слагаемое правой части показывает эффект замены, а второе – эффект дохода Выпишем уравнение Слуцкого для рассмотренной выше задачи потребительского выбора с функцией полезности 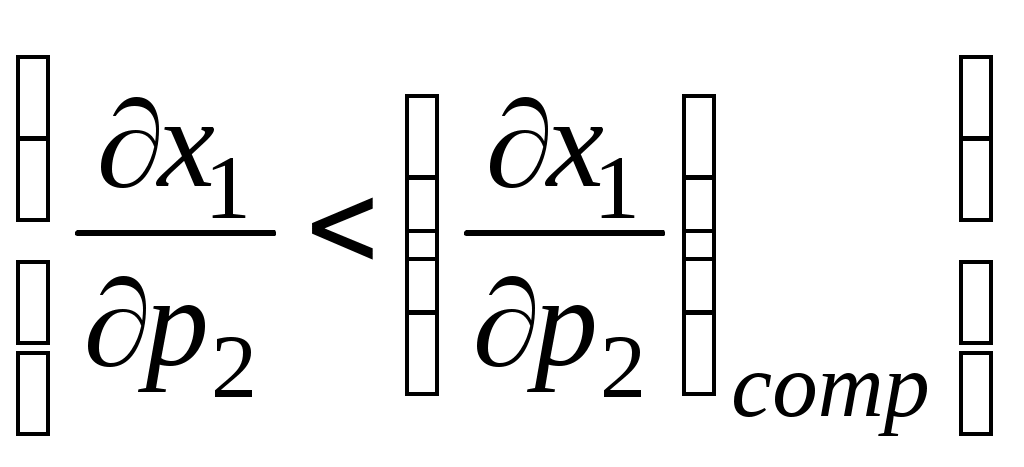 , если i=1,j=2: .  ,  спрос на благо х1 растет при росте дохода. Поэтому, согласно уравнению Слуцкого спрос на благо x1 будет расти больше при наличии компенсации  .Так как,  , и  , то товары 1 и 2 взаимозаменяемы, но представляются независимыми без учета компенсации.Поскольку  , а  , то на покупку первого блага потребитель всегда будет расходовать 0.484 часть своего дохода, а на покупку второго блага: 0.516 часть своего дохода, независимо от цен этих благ. Т.к.  , то потребитель второй товар предпочитает первому.Замечание. Решение задачи минимизации расходов при заданном уровне полезности дает возможность построить функции компенсированного спроса потребителя. Так, при построении модели минимизации расходов мы исходили из предпосылки, что цены благ и требуемый уровень полезности являются постоянными величинами. Однако с течением времени цены на рынке растут или падают, а желаемый уровень полезности также может измениться. В зависимости от этого будет меняться и количество каждого из благ, которые потребитель приобретает на рынке. Поэтому если решить систему уравнений в общем виде (не приписывая ценам и требуемому уровню полезности конкретные числовые значения), то оптимальные количества каждого блага предстанут как функции от цен и желаемого потребителем уровня полезности:  Эти функции также являются функциями спроса на блага, так как отражают зависимость между количеством благ, приобретаемых потребителем на рынке, и другими факторами.Заметим, однако, что в отличие от функций спроса, полученных при решении задачи максимизации полезности, когда количество приобретаемых товаров зависело от цен и от дохода, функции спроса, полученные при решении задачи минимизации расходов, отражают зависимость количества приобретаемых товаров от цен на эти товары, а также от некоторого фиксированного уровня полезности, на котором должен оставаться потребитель, потребляя тот или иной набор благ. Такие функции называются функциями компенсированного спроса, или хиксианскими, в честь знаменитого экономиста Джона Хикса. В целом анализ потребительского спроса дает возможность правильно классифицировать товары с целью последующей разработки оптимальной ценовой и товарной стратегии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
