Уч пособие ЭМС_2. Е. М. Виноградов
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
9.7.2.Оценка уровней интермодуляционных продуктов | |||||||||||||||||||||||||||||||||||||||||||||||
| Двухсигнальная интермодуляция 3-го порядка: fим = 2fv– fi | ||
| f, МГц | a | b |
| 0 < f 0.8 | 10.8 | 2.1 |
| 0.8 < f 5.5 | 9.3 | 4.0 |
| f > 5.5 | 13.4 | 3.2 |
| Двухсигнальная интермодуляция 5-го порядка: fим = 3fv– 2fi | ||
| 0 < f 1.5 | 31 | 11.4 |
| f > 1.5 | 36 | 7.5 |
9.7.3. Оценка интермодуляции в радиоприемниках
Интермодуляционные продукты в РПУ могут быть образованы очень большим числом частот, которые присутствуют в эфире. В связи с этим возникает вопрос, в какой полосе частот относительно частоты настройки приемника следует рассматривать мешающие сигналы, которые могут образовать опасные интермодуляционные продукты. Обзор данных измерений и практический опыт показывают, что выше некоторых значений расстроек мешающих сигналов, зависящих от типа оборудования, вероятность нелинейных эффектов в приемнике незначительна. При известной АЧХ входного фильтра или преселектора приемника в качестве полосы частот, в пределах которой выполняется анализ сигналов на нелинейные эффекты, может быть использована ширина полосы пропускания входного фильтра или преселектора приемника на некотором уровне, например, на уровне 30 дБ. Если информация о характеристиках частотной избирательности отсутствует, можно использовать результаты статистической обработки экспериментальных данных относительно максимальной частотной расстройки помехи fmax, при которой наблюдалось образование интермодуляционных продуктов в приемниках. В [16], [32] приведены интегральные функции распределения для fmax, полученные на ограниченном множестве приемников для интермодуляции 3-го порядка в диапазонах ВЧ, ОВЧ, УВЧ. Эти функции распределения позволяют, в частности, установить, что с вероятностью 0.75 расстройка fmax для сигналов, образующих ИМП 3-го порядка не превысит значений, приведенных в табл. 9.4.
Таблица 9.4
Границы частотных интервалов для анализа нелинейных эффектов в приемнике
| Частота настройки приемника f0R | f0R < 30 МГц | 30 f0R< 300 МГц | f0R>300 МГц |
| Максимальная расстройка fmax | f0R/2 | f0R/3 | f0R/10 |
Эти значения fmax могут быть использованы для определения границ частотного интервала, в котором рассматриваются нелинейные эффекты в общем случае.
Значения максимальных расстроек, приведенные в табл. 9.4, в определенной степени можно считать условными. Они дают некоторый ориентир на порядок расстроек, превышение которых при образовании интермодуляционной помехи маловероятно. На практике могут использоваться другие значения. Так, например, при исследовании ЭМС радиоэлектронных средств, размещаемых на объекте, в диапазоне частот 225…400 МГц с использованием модели Cosam полоса частот, в которой рассматривались мешающие сигналы на возможные нелинейные эффекты в РПУ, была выбрана для всех средств одинаковой: fmax = 20 МГц [25].
Интермодуляционная помеха, образующаяся в приемнике, является потенциально опасной, если ее частота находится в полосе пропускания приемника, т. е. если выполняется условие
| fим – f0R | Bпч/2 (9.67)
где fим – частота интермодуляционного продукта (помехи); f0R – частота настройки приемника; Bпч – полоса пропускания тракта последней ПЧ.
Окончательное решение о степени опасности интермодуляционного продукта может быть принято на основании оценки его уровня. Обычно в приемнике рассматривают двухсигнальные продукты третьего порядка с частотами интермодуляции | 2fi– fj |. В ряде случаев в число анализируемых продуктов включают трехсигнальный продукт третьего порядка с частотой интермодуляции | fi– fj+ fk | или двухсигнальный продукт пятого порядка с частотой |3fi– 2fj |, а для некоторых типов приемников, например приемников с преобразованием несущей частоты на нулевую промежуточную частоту, ИМП второго порядка вида | fi– fj |, где fi, fj, fk – частоты мешающих сигналов на входе приемника.
Модели для анализа интермодуляции в РПУ в ряде случаев могут использовать информацию о характеристиках приемника, которая отсутствует в спецификациях на приемник. Такие модели требуют дополнительных измерений некоторых характеристик приемников.
Пусть fим = | nf1 mf2 |, где n, m – целые положительные числа и
m + n= N – порядок интермодуляции. Если известна точка пересечения N-го порядка (или динамический диапазон по интермодуляции порядка N, из которого можно получить оценку точки пересечения), оценить уровень интермодуляционного продукта можно, используя (9.45):
PIMN = nP1 + mP2 – (n + m – 1)IPNi, (9.45)
где PIMN – мощность ИМП N-го порядка, приведенная к входу приемника, дБм; P1, P2 – мощности сигналов на входе приемника на частотах f1, f2, соответственно, дБм; IPNi – точка пересечения N-го порядка, отнесенная к входу приемника, дБм.
Это выражение определяет уровень ИМП, приведенный к входу приемника, для наихудшего случая, когда fим = f0R, а взаимодействующие сигналы представляют собой немодулированные несущие. В общем случае возможна коррекция уровня ИМП, определенного из (9.45). Коррекция может быть связана с расстройкой частоты интермодуляции относительно частоты настройки приемника, а также с наличием модуляции у взаимодействующих сигналов.
В определенных ситуациях могут быть использованы эмпирические модели. В [31] представлены эмпирические модели для оценки уровней ИМП, возникающих в приемниках, рабочие частоты которых не превышают 1 ГГц. Модели использовались в автоматизированной программе назначения частот для оперативных групп наземных подвижных средств. Модели рассматривают двух и трехсигнальную интермодуляцию третьего и пятого порядков, вид которой и расчетные формулы для оценки мощности интермодуляционных продуктов представлены в табл. 9.5.
Таблица 9.5
Эмпирические модели для оценки эффекта интермодуляции в радиоприемниках
| № п/п | Вид интермодуляции | Мощность продукта интермодуляции, дБм |
| 1. | 2f1 – f2 | 2P1 + P2 – 10 – 60 lg(dF) |
| 2. | f1 – f2 + f3 | P1 + P2 + P3 – 81 lg(dF) |
| 3. | 3f1 – 2f2 | 3P1 + 2P2 – 57 – 135 lg(dF) |
| 4. | 2f1 – 2f2 + f3 | 2P1 + 2P2 + P3 – 132 – 195 lg(dF) |
В табл. 9.5 обозначено: Pi – мощность, поступающая на вход приемника на частоте fi (i=1, 2, 3), дБм;
n – число сигналов, образующих ИМП (n= 2, 3);
fi = | f0R– fi |, МГц .
Двухсигнальная интермодуляция третьего порядка является наиболее опасным видом интермодуляции, и в современных программных средствах анализа ЭМС всегда исследуется степень опасности продуктов интермодуляции этого вида. В дальнейшем остановимся только на моделях, связанных с двухсигнальной интермодуляцией 3-го порядка, частота которой fим и частоты нежелательных сигналов f1 и f2, образующих ее, связаны соотношением:
fим = 2f1 – f2 (9.68)
Большинство моделей, предлагаемых для оценки уровней или степени опасности продуктов интермодуляции, образующихся в приемнике, требуют информации о параметрах приемника, которая отсутствует в спецификациях на приемник. Поэтому выполнить необходимые расчеты, используя эти модели, можно только после дополнительных измерений на приемнике. Так, например, в документах МСЭ [35], [36] предложена модель для оценки мощности ИМП 3-го порядка в виде:
PIM3 = 2(P1 – β1) + (P2 – β2) – K2,1 , (9.69)
где PIM3 – эквивалентный уровень мощности ИМП 3-го порядка на входе приемника на частоте его настройки, дБм; P1, P2 – мощности нежелательных сигналов на частотах f1, f2, соответственно, на входе приемника, дБм; β1, β2 – ослабление нежелательных сигналов на частотах f1, f2, соответственно, во входном фильтре приемника, вызванное их расстройкой относительно частоты настройки приемника, дБ; K2,1 – потери преобразования нежелательных сигналов в интермодуляционный продукт 3-го порядка.
Выражение (9.69) представляет частный случай расчета мощности двухсигнальных ИМП, предложенный в модели Cosam [25]. Чтобы использовать (9.69) для вычисления мощности ИМП, необходимо знать характеристику частотной избирательности входных цепей приемника β(Δf) и потери преобразования K2,1. Чаще всего ни характеристика частотной избирательности, ни потери преобразования неизвестны. В [36] предложено описание характеристики частотной избирательности приемника β(Δf) [дБ]по высокой частоте в виде
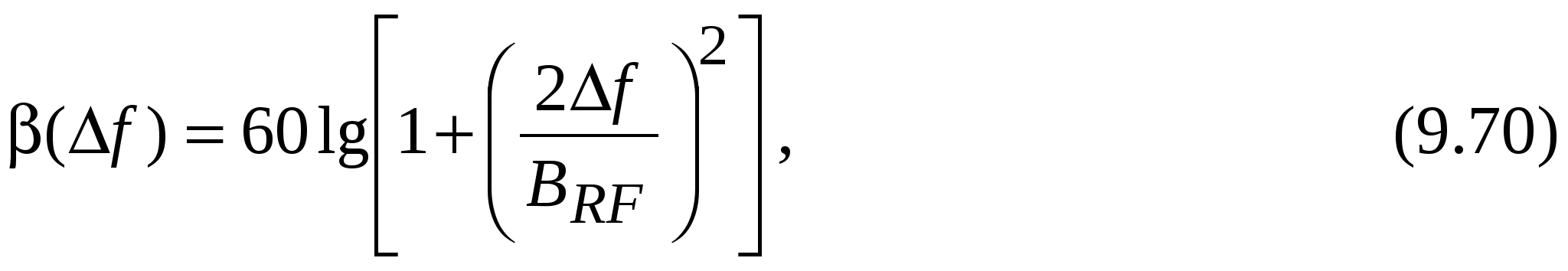
где BRF – ширина полосы приемника на радиочастоте.
Однако, даже при использовании (9.70) необходимо измерить значение K2,1 и получить информацию о BRF.
Оценка степени опасности интермодуляционных продуктов, возникающих в приемнике, может быть основана на сравнении взвешенной суммы мощностей мешающих сигналов на входе приемника с некоторым порогом. Весовые коэффициенты определяются множителями перед частотами сигналов, образующими ИМП, а порог зависит от восприимчивости приемника к интермодуляции третьего порядка.
Так, для рассматриваемого вида интермодуляции, при условии, что уровень полезного сигнала и уровень ИМП 3-го порядка не превышают порога срабатывания АРУ приемника, мощность ИМП, приведенную к входу приемника, можно оценить, используя выражение [16], [32], [33]:
PIM3 = 2P1 + P2 + PR(f0R) 3I(f1, f2), (9.71)
где P1, P2 – мощности сигналов, образующих ИМП, на входе приемника, дБм; PR(f0R) – чувствительность приемника на частоте его настройки f0R, дБм; I(f1, f2) – восприимчивость приемника к интермодуляции 3-го порядка, полученная двухсигнальным методом и соответствующая рассматриваемой расстановке частот, дБм.
Интермодуляционная помеха считается опасной, если ее мощность, приведенная к входу приемника, превышает чувствительность приемника. Если характеристика I(f1, f2) соответствует kим = 1, то условие PIM3 PR(f0R), приводит к соотношению
2P1 + P2 3I(f1, f2) (9.72)
Разность между левой и правой частями выражения (9.72) (если она неотрицательная) определяет минимально необходимое значение подавления интермодуляционной помехи, при котором мощность ИМП, приведенная к входу приемника, не превысит чувствительность приемника.
При использовании выражения (9.72) в качестве критерия опасности двухсигнального ИМП 3-го порядка необходимо знать (или измерить) характеристику восприимчивости I(f1, f2).
В общем случае восприимчивость приемника к интермодуляции зависит не только от расстановки частот мешающих сигналов на частотной оси, но и от уровня полезного сигнала. Учесть влияние полезного сигнала можно, используя характеристику частотной избирательности по интермодуляции, снятую трехсигнальным методом. В этом случае интермодуляционная помеха считается опасной, если выполняется соотношение аналогичное (9.72), а именно:
2P1 + P2 3W(f), (9.73)
где W(f) – восприимчивость к интермодуляции 3-го порядка, полученная трехсигнальным методом, дБм; f = | f0R f1 | расстройка ближайшего к частоте настройки приемника мешающего сигнала,
В [20] для описания характеристики W(f) предложено использовать модель вида:
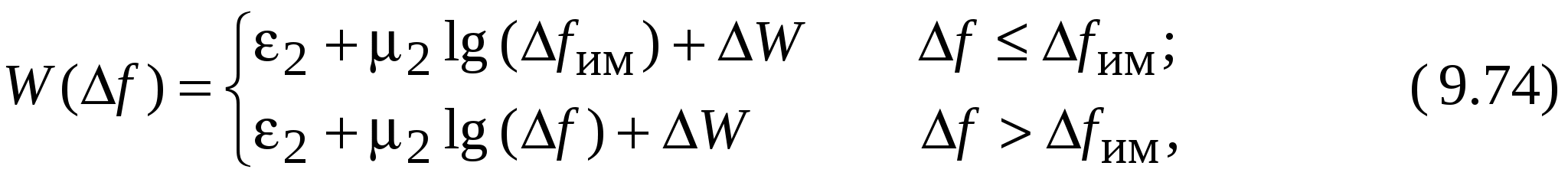
где 2 [дБм], 2 [дБ/дек], fим – параметры, получаемые из характеристики избирательности по интермодуляции 3-го порядка, снятой трехсигнальным методом; W – поправка на восприимчивость к интермодуляции 3-го порядка при превышении полезным сигналом чувствительности приемника, дБ.
Параметры 2, 2, fим получают посредством кусочно-линейной аппроксимации характеристики частотной избирательности по интермодуляции 3-го порядка, снятой трехсигнальным методом, при уровне полезного сигнала равном чувствительности приемника. В этом случае поправка W = 0 дБ. Для получения поправки W используют линейную аппроксимацию зависимости восприимчивости приемника к продукту интермодуляции 3-го порядка от уровня полезного сигнала. Эту зависимость получают при фиксированной расстановке частот сигналов, образующих интермодуляционный продукт. Обычно сигнал, ближайший к частоте настройки приемника, находится во втором соседнем канале. Общий вид перечисленных характеристик показан на рис. 9.28 и 9.29.
Н
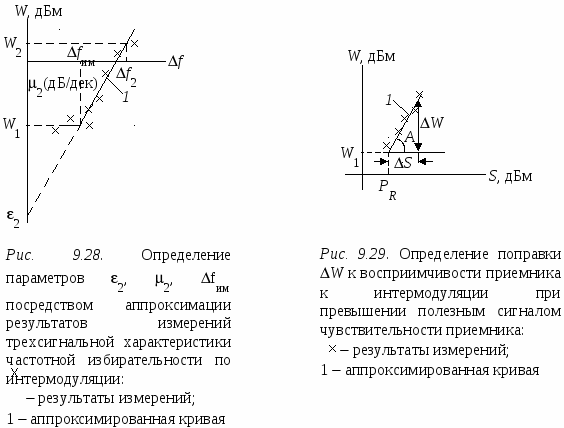
а рис. 9.28 представлена характеристика частотной избирательности по интермодуляции. Когда сигналы, образующие ИМП, находятся в полосе тракта первой ПЧ, но за пределами полосы тракта конечной ПЧ, восприимчивость приемника к интермодуляции 3-го порядка меняется мало (см. поведение точки пересечения IP3 на рис.9.19) и может быть аппроксимирована постоянным значением. При увеличении расстройки мешающих сигналов восприимчивость приемника к продукту интермодуляции изменяется достаточно сильно, и этот участок аппроксимируют прямой. Точка излома характеристики избирательности определяет параметр fим. Параметры 2 и 2 определяют аналогично параметрам 1 и 1 для характеристики частотной избирательности по блокированию, используя выражения (9.53) и (9.54) с заменой в них 1 на 2, 1 на 2 и Pнi на Wi, где Wi – значение восприимчивости приемника к интермодуляции при расстройке ближайшего сигнала, образующего ИМП, равной fi.
Характеристика, представленная на рис. 9.29, где PR обозначена чувствительность приемника, снимается также трехсигнальным методом. Изменяя уровень полезного сигнала S на входе приемника, определяют уровень мешающих сигналов W (одинаковый для обоих сигналов), при котором отношение сигнал/шум на выходе приемника изменяется на то же самое значение, на какое оно изменялось при снятии частотной характеристики избирательности по интермодуляции W(Δf). Линейная аппроксимация результатов измерений позволяет получить значение
dим = tg A = W/S,
откуда W = dим S (9.75)
Рассмотренная методика относится к интермодуляции 3-го порядка и представляется достаточно сложной для реализации. Однако она учитывает трехсигнальный характер интермодуляции и лучше отражает реальную ситуацию, в которой происходит прием полезных сигналов. При создании соответствующей базы данных для радиоприемных устройств она может найти практическое применение.
В стандартах на современные радиотехнологии, использующие в системах связи цифровые сигналы, определены требования к параметру, который именуется подавлением интермодуляционного отклика третьего порядка в приемниках. Этот параметр может быть использован для оценки уровня ИМП.
По определению [34], подавление интермодуляционного отклика является мерой способности приемника принимать полезный модулированный сигнал с заданным качеством в присутствии двух или большего числа нежелательных сигналов при определенной расстановке их частот относительно частоты полезного сигнала. Численно подавление интермодуляционного отклика в приемнике определяется разностью (в децибелах) между уровнями нежелательных сигналов, образующих интермодуляционную помеху определенного уровня, и полезным сигналом.
И
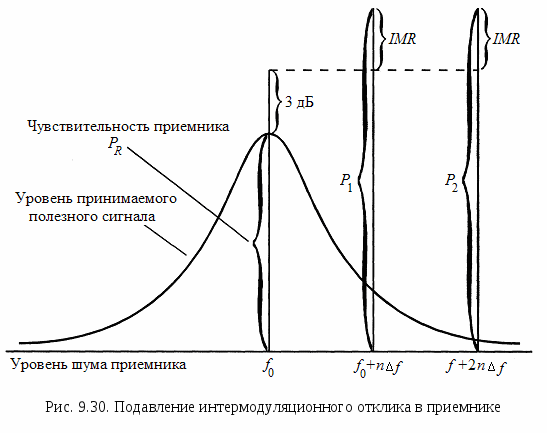
змерение подавления интермодуляционного отклика проводят трехсигнальным методом. При измерении уровень испытательного сигнала, который исполняет роль полезного сигнала, устанавливают на 3 дБ выше чувствительности приемника. Два нежелательных сигнала одинакового уровня размещают на оси частот так, чтобы частота образовавшегося интермодуляционного продукта совпала с частотой полезного сигнала. Эту ситуацию поясняет рис. 9.30. Уровни нежелательных сигналов увеличивают до тех пор, пока качество полезного сигнала на выходе приемника не станет таким же, как при приеме полезного сигнала с уровнем равным чувствительности приемника в отсутствие внешних помех. Для цифровых сигналов это качество определяется значением BER.
По определению, при P1 = P2 = P[дБм] подавление интермодуляционного отклика IMR[дБ] составит:
IMR = P (PR+ 3)
С другой стороны, как следует из общей теории интермодуляции (см., например, выражение (9.24) для N = 3, k= 1):
PIM3 = 2P1 + P2 +LP (9.76)
Когда уровень ИМП достигнет уровня шума приемника, при полезном сигнале, который на 3 дБ выше чувствительности приемника, качество приема будет таким же, как и при сигнале равном чувствительности приемника. Принимая для рассматриваемых сигналов в качестве уровня отсчета уровень собственных шумов приемника, и учитывая, что при измерениях P1 = P2 = P, из (9.76) получим:
0 = 3P + LP = 3(PR + 3 + IMR) + LP
или LP = –3(PR + 3 + IMR).
Подставив значение LP в (9.76), окончательно найдем:
PIM3 = 2P1 + P2 3IMR 3PR 9 (9.77)
Используя в этом выражении значения уровней нежелательных сигналов на входе приемника P1, P2 и чувствительности приемника PR, выраженные в децибелах относительно милливатта, подавление интермодуляционного отклика IMR в децибелах, получим значение PIM3, выраженное в децибелах относительно уровня собственного шума приемника.
Если интермодуляционные продукты на частоте настройки приемника образованы несколькими парами нежелательных сигналов, то результирующая мощность интермодуляционной помехи оценивается как сумма мощностей этих продуктов.
Для современных систем радиосвязи, использующих цифровые сигналы, требования к подавлению интермодуляционного отклика формулируются в стандартах на эти системы в разделе, где рассматриваются граничные значения параметров радиоприемных устройств. В общем случае значения IMR зависят от расстройки мешающих сигналов. Обычно измерения выполняют, когда расстройка нежелательных сигналов составляет не менее двух каналов по сетке частот, принятой для радиотехнологии. Так для систем, использующих ширину канала 12,5 кГц, 20 кГц, 25 кГц, расстройку между нежелательными сигналами при измерениях IMR берут 25 кГц, для стандарта GSM 800 кГц и т. п. Типичные значения IMR составляют 70 дБ для оборудования базовых станций и 65 дБ для мобильного и носимого оборудования.
9.7.4. Оценка перекрестных искажений
Перекрестные искажения от модулированных мешающих сигналов проявляются в форме перекрестной амплитудной модуляции, амплитудно-фазовой конверсии или комбинации указанных видов искажений.
Амплитудно-фазовая конверсия имеет место, когда усилительные приборы, используемые в радиоприемных устройствах, обладают нелинейными амплитудно-фазовыми характеристиками. Это свойство характерно для ряда приборов СВЧ. Исследование нелинейных искажений в таких приборах при узкополосных входных сигналах можно выполнить, заменив амплитудную и амплитудно-фазовую нелинейные характеристики прибора на две ортогональные нелинейные амплитудные характеристики. В этом случае результаты, полученные для амплитудных нелинейностей, можно использовать для исследования искажений, связанных с амплитудно-фазовой конверсией.
Перекрестная амплитудная модуляция характерна для области более низких частот, чем диапазон СВЧ, где фаза сигналов на выходах устройств не зависит от амплитуды входного сигнала. Перекрестная амплитудная модуляция имеет место, если при изменении амплитуды мешающего сигнала меняется коэффициент усиления усилительных устройств в тракте приемника. Обычно это происходит в усилителе высокой частоты. Это означает, что перекрестная амплитудная модуляция происходит, когда уровень мешающего сигнала таков, что имеет место эффект блокирования. Глубину перекрестной амплитудной модуляции можно оценить, используя выражение [4]
где mпер – глубина перекрестной амплитудной модуляции; mi – глубина амплитудной модуляции помехи; IP3i – точка пересечения третьего порядка, отнесенная к входу приемника, мВт; I –помеха на входе приемника, мВт.
Учитывая, что перекрестная амплитудная модуляция сопровождается блокированием приемника, современные программные средства, выполняющие анализ ЭМС РЭС, которые работают в диапазоне частот, не превышающем верхней границы диапазона УВЧ, не анализируют эффект перекрестной модуляции, ограничиваясь анализом эффекта блокирования. Если в результате такого анализа установлено, что внешняя помеха блокирует приемник, то мероприятия, направленные на устранение эффекта блокирования, приводят также и к устранению перекрестной амплитудной модуляции.

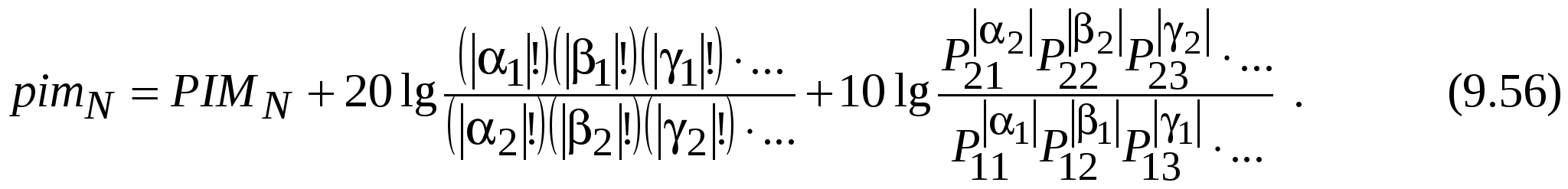
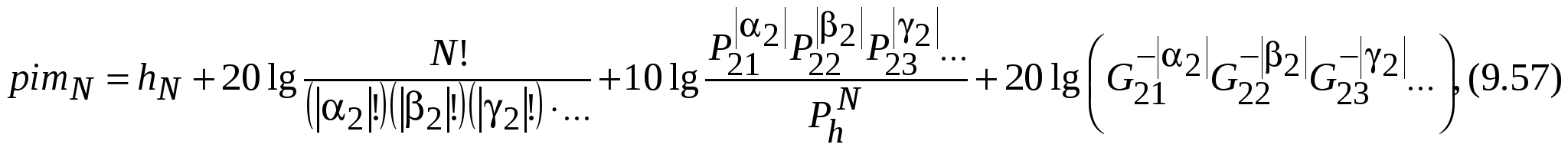 где |2|+|2|+|2|+…= N – порядок интересующего ИМП; hN – уровень мощности N-й гармоники [дБВт]; Ph –мощность на основной частоте, при котором N-я гармоника равна hN (Вт); G2i (i = 1, 2, 3,…) – выраженные относительными числами пик-факторы сигналов, участвующих в образовании интересующего ИМП.
где |2|+|2|+|2|+…= N – порядок интересующего ИМП; hN – уровень мощности N-й гармоники [дБВт]; Ph –мощность на основной частоте, при котором N-я гармоника равна hN (Вт); G2i (i = 1, 2, 3,…) – выраженные относительными числами пик-факторы сигналов, участвующих в образовании интересующего ИМП.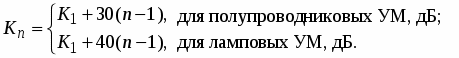
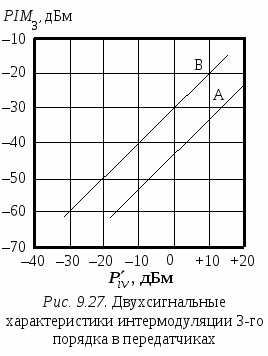 оскольку частота помехи в это выражение входит с коэффициентом 1, то можно ожидать, что в определенных пределах изменения уровня
оскольку частота помехи в это выражение входит с коэффициентом 1, то можно ожидать, что в определенных пределах изменения уровня