Уч пособие ЭМС_2. Е. М. Виноградов
 Скачать 3.78 Mb.
|
Особенности описания антенных устройств в задачах ЭМСИнформации, которая приведена об антеннах в антенных спецификациях, обычно недостаточно для анализа ЭМС РЭС в широкой полосе частот. Основная характеристика антенны, ее диаграмма направленности, имеет сложную структуру и зависит от многих факторов:
Вокруг антенны можно выделить три зоны: I. В непосредственной близости от антенны находится зона реактивного ближнего поля, в которой доминируют неизлучаемые, быстро убывающие с расстоянием от антенны компоненты квазистатического поля. Для электрически малых антенн (т. е. для антенн, размеры которых малы по сравнению с длиной волны) реактивное ближнее поле простирается примерно до расстояния d ≈ λ/2π от антенны. Граница реактивного ближнего поля зависит от формы и конструкции антенны. Для антенн, имеющих значительный электрический размер, часто полагают, что граница реактивного поля простирается примерно до расстояния  ,где D – наибольший размер антенны. За пределами области ближнего неизлучаемого реактивного поля выделяют две зоны излучаемого поля: ближнюю и дальнюю. II. Ближняя зона находится между зоной реактивного поля и дальней зоной излучаемого поля. В ближней зоне преобладает излучаемое поле, однако относительное распределение поля по разным направлениям зависит от расстояния от антенны. В этой зоне ДНА еще не сформировалась и при оценке ЭМС она не учитывается. III. Дальняя зона характеризуется тем, что здесь относительное распределение поля практически не зависит от расстояния до антенны и определяется только угловыми координатами точки, в которой рассматривается поле. В этой зоне считают, что ДНА сформировалась, и ее можно использовать для оценки уровней помех, возникающих между радиопередающими и радиоприемными устройствами в этой зоне. Ближнюю зону излучаемого поля часто называют зоной Френеля, а дальнюю зону зоной Фраунгофера. Для электрически больших антенн с широкой апертурой и высокой направленностью расстояние, с которого начинается дальняя зона, определяется как  ,где D – максимальный размер апертуры антенны; λ – длина волны электромагнитного поля. Если в формировании ДНА принимают участие элементы окружения антенны, то D представляет максимальный размер излучающей структуры. Для слабонаправленных антенн с низким коэффициентом усиления (G < 10 дБ) граница, с которой начинается дальняя зона, оценивается как d > 3λ
Из сказанного следует, что для оценки уровней помех, возникающих между радиопередающими и радиоприемными устройствами, диаграммы направленности антенн могут быть использованы только, когда антенны находятся в дальней зоне. Большое число факторов, влияющих на форму ДНА, особенно в области боковых лепестков, не позволяют точно описать диаграмму направленности антенны, используя детерминированные функции. Поэтому в ряде случаев, особенно при статистическом анализе ЭМС, используют статистическое описание диаграмм направленности антенн. Тем не менее, несмотря на все недостатки детерминированного описания, детерминированные модели диаграмм направленности антенн сегодня используются наиболее часто. Хотя усиление антенны это свойство, присущее самой антенне, и оно не включает потерь, связанных с рассогласованием антенно-фидерного тракта с антенной, и потерь, обусловленных несовпадением поляризаций антенны и внешнего электромагнитного поля, но при анализе ЭМС эти факторы не могут быть оставлены без внимания. От них зависит уровень непреднамеренных помех между радиоэлектронными средствами, использующими антенные устройства.
Математическое описание ДНА используется при оценке уровней сигналов и помех, поступающих на входы радиоприемных устройств в анализируемой совокупности РЭС. Диаграмма направленности формируется в дальней зоне излучения антенны. Поэтому она используется только при оценке ЭМС РЭС, расположенных в дальней зоне по отношению друг к другу. Поскольку форма ДНА зависит от частоты, при описании диаграммы направленности выделяют две области: область рабочих частот антенны и область нерабочих частот антенны. Рассмотрим описание ДНА в каждой из этих областей отдельно. 10.3.1. ДНА в области рабочих частот.В этой области форма ДНА изменяется в допустимых пределах, и при расчетах эти изменения не учитывают, считая, что форма ДНА в рабочей полосе частот антенны не изменяется. В 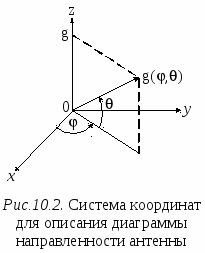 сферической системе координат диаграмма направленности является функцией, описывающей значение коэффициента усиления антенны в зависимости от направления прихода электромагнитной волны, g(, ) (рис. 10.2). При описании обычно полагают, что направление максимального излучения (приема) ДНА совпадает с направлением оси x, от которой в плоскости xoy отсчитывается азимутальный угол . Угол места θ, в отличие от классической сферической системы координат, где он отсчитывается от оси z, при описании ДНА отсчитывают от плоскости xoy. Такая система отсчета углов используется для описания координат точек земной поверхности. В ней угол представляет долготу, а θ – широту точки на поверхности земли. Диаграмму направленности антенны можно записать в виде: g(, ) = g0 gN(, ), (10.2) где g0 – максимальный коэффициент усиления антенны; gN(, ) – нормированная ДНА, значения которой лежат в интервале [0,1], и gN(0, 0)=1. Хотя описание ДНА в относительных единицах используется достаточно часто, в инженерных расчетах диаграмму направленности обычно описывают в децибелах относительно изотропной антенны [dBi], которые часто обозначают просто дБ: G(, ) = G0+GN(, ), (10.3) где G(, ) – диаграмма направленности антенны, dBi; G0 – максимальный коэффициент усиления антенны, dBi; GN(, ) – нормированная ДНА, значения которой GN(0, 0) = 0, GN(, ) ≤ 0 и выражены в децибелах относительно G0. При анализе ЭМС совокупности РЭС, размещенных в дальней зоне, необходимо располагать информацией о трехмерных диаграммах направленности антенн, которые используют исследуемые средства. Обычно имеется информация только о двух ортогональных сечениях ДНА в горизонтальной и в вертикальной плоскости, т. е. GH() = G(, 0) и GV() = G(0, ). Их соответственно называют диаграммой направленности в горизонтальной и диаграммой направленности в вертикальной плоскости. ДНА в горизонтальной и в вертикальной плоскости получают либо посредством измерений, либо на основе теоретического анализа. Эти диаграммы используются для построения трехмерной ДНА, а точнее, для определения коэффициента усиления антенны в направлении, которое не лежит ни в одной из исходных плоскостей. Обычно в качестве исходного материала используют нормированные ДНА в горизонтальной и в вертикальной плоскости. Получив с их помощью значение GN(,), вычисляют G(, ), используя (10.3). Предварительно диаграммы направленности в горизонтальной и в вертикальной плоскости приводят к виду, удобному для дальнейшей работы. ДНА делят на две области: область главного лепестка и область боковых и задних лепестков. ДНА в области главного лепестка аппроксимируют удобной аналитической функцией. Если ДНА получена по напряженности поля, то в качестве такой функции могут быть использованы прямоугольная функция, трапецеидальная функция, exp[–1.39(x/x0)], cos2[1.14(x/x0)], sin[2.81(x/x0)]/[2.81(x/x0)] и др. Здесь x – угол в плоскости (горизонтальной или вертикальной), для которой производится аппроксимация ДНА; x0 – ширина ДНА в соответствующей плоскости на уровне –3 дБ. Для ДНА, полученных по мощности, при аппроксимации главного лепестка также используют прямоугольную или трапецеидальную функции, или квадрат функций, перечисленных выше. Следует заметить, что с помощью указанных функций сечения нормированной ДНА определяют усиление в относительных единицах (не в децибелах). В спецификациях на антенну обычно указывают ширину главного лепестка ДНА в горизонтальной и в вертикальной плоскостях на уровне –3 дБ. Если данных для аппроксимации главного лепестка недостаточно, можно использовать то обстоятельство, что ширина главного лепестка на уровне –10 дБ примерно в два раза больше, чем на уровне –3 дБ. Для систем радиосвязи CEPT выделяет девять типов направленных антенн, разбитых на четыре группы, которые используются на практике в системах подвижной и фиксированной связи. Для каждого типа предложена математическая модель, описывающая сечение ДНА, которое может быть использовано для представления диаграммы направленности антенны в горизонтальной и/или вертикальной плоскости [37]. В 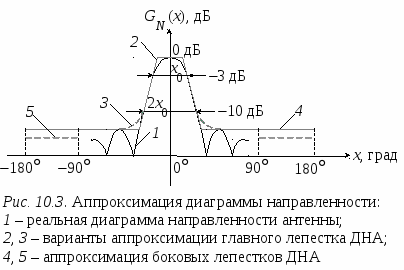 области боковых и задних лепестков ДНА чаще всего аппроксимируют некоторым постоянным уровнем. Значение этого уровня выбирают, используя статистику измерений коэффициента усиления по боковым и задним лепесткам для конкретного типа антенны, либо на основании теоретических исследований. Часто постоянный уровень соответствует максимальному уровню боковых лепестков. В некоторых случаях для антенн с высокой направленностью уровни, моделирующие лепестки диаграммы направленности в передней и задней полусферах ДНА, могут различаться. Пример построения такой ДНА в декартовой системе координат показан на рис.10.3. На рис. 10.4 представлен в полярных координатах один из образцов сечений ДНА, рекомендуемых CEPT для оценки ЭМС при координации частотных присвоений системам мобильной и фиксированной связи в приграничных районах. Если ГЛ ДНА обладает круговой симметрией (ДНА игольчатого типа), то для ее пространственного описания достаточно одного сечения. Угол относительно оси, соответствующей максимальному коэффициенту усиления в данном сечении, полностью определяет усиление антенны и в любом другом направлении, не лежащем в плоскости сечения, но имеющем такой же угол прихода электромагнитной волны, как и рассматриваемый. В 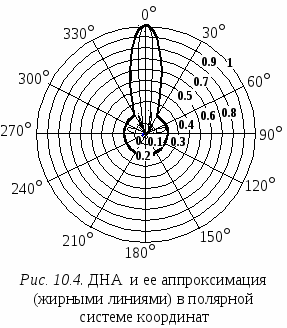 том случае, когда круговая симметрия отсутствует, но ДНА имеет относительно узкий главный лепесток, как в горизонтальной, так и в вертикальной плоскости, коэффициент усиления по главному лепестку может быть получен на основе эллиптической аппроксимации поперечных сечений главного лепестка, как это показано на рис 10.5. Для этого нормированные в горизонтальной и вертикальной плоскостях ДНА квантуют по уровню. Для каждой плоскости уровни квантования берут одинаковыми. Ширина диаграмм направленности на этих уровнях определяет оси эллипсов, описывающих сечение ДНА. Каждый уровень усиления определен границами двух эллипсов. Задача состоит в том, чтобы определить, между границами каких эллипсов лежит направление луча, для которого ищется коэффициент усиления антенны. Обозначим i и i ширину ДНА в горизонтальной и в вертикальной плоскости на i-ом уровне квантования, соответственно. Для луча, направление которого определяет пара углов (, ), эти углы сравнивают с полуосями (i/2, i/2) каждой эллиптической границы. Если > i/2 или > i/2, этот эллипс из рассмотрения исключают. В качестве коэффициента усиления GN(, ) выбирают значение усиления, соответствующее первому эллипсу, полуоси которого не меньше координат луча ( i/2, i/2), а координаты луча (, ) удовлетворяют неравенству: 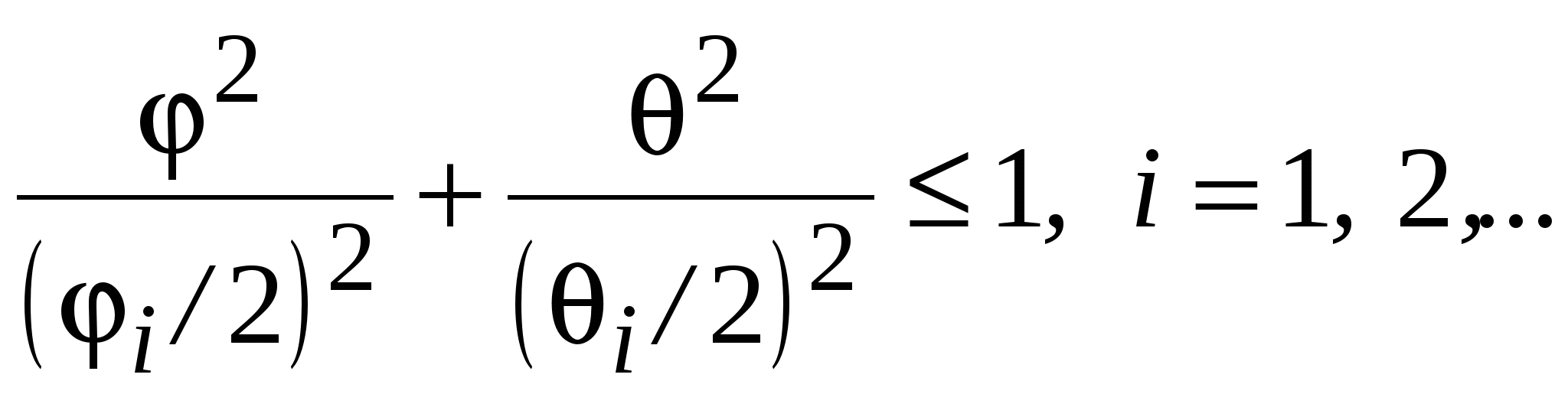 Если луч лежит за пределами главного лепестка, коэффициент усиления антенны принимается равным коэффициенту усиления по боковым (задним) лепесткам. Получив значение GN(, ), окончательный коэффициент усиления устанавливают, используя соотношение (10.3). Другой метод описания ДНА предполагает, что диаграмма в горизонтальной плоскости на каждом азимуте φ формируется наклоненной на угол θ вертикальной диаграммой направленности. В этом случае формула для оценки коэффициента усиления антенны имеет вид: G(, ) = G0 + GH() + GV(), (10.4) где GH(), GV() – нормированные ДНА в горизонтальной и вертикальной плоскости, соответственно, дБ. Эта формула ориентирована на антенны, у которых диаграмма направленности в горизонтальной плоскости близка к круговой. Однако, ввиду ее простоты, формулу часто используют и для направленных антенн. Н 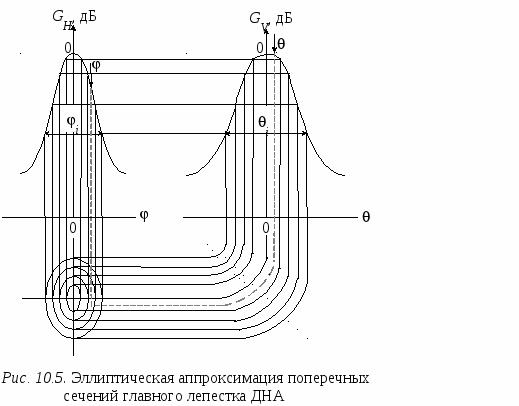 аконец, для фиксированной службы в предположении, что диаграммы направленности антенны в горизонтальной и вертикальной плоскостях являются симметричными, используя [38], выражение для вычисления GN(, ), дБ, можно представить взвешенной суммой нормированных коэффициентов усиления GH() и GV(), дБ:  Теперь из (10.3), можно вычислить G(, ). 10.3.2. ДНА на нерабочих частотахВ диапазоне частот, который для антенны рассматривается как диапазон ее рабочих частот, максимальное значение коэффициента усиления антенны считают постоянным. Его значение всегда указывают в спецификациях на антенну. Изменение усиления антенны на частотах, лежащих вне рабочего диапазона частот антенны, в спецификациях на антенну не приводят, и оно не регламентируется нормативными документами. В области частот, лежащих вне рабочего диапазона, диаграмма направленности антенны расширяется, и коэффициент усиления антенны падает. При анализе ЭМС нужно учитывать оба эти обстоятельства. Математические модели, описывающие изменение коэффициента усиления антенны на нерабочих частотах, обычно получают на основе анализа и обработки результатов специально организованных измерений. Вид модели, который может быть использован для описания зависимости коэффициента усиления от частоты, может быть разным. Одно из используемых описаний коэффициента усиления по главному лепестку ДНА в общем случае имеет вид: G(f) = G0 + Cilg (f / fгрi) +Di, (10.6) где G(f) – коэффициент усиления по главному лепестку на частоте f за пределами рабочего диапазона частот антенны, дБ; G0 – коэффициент усиления по главному лепестку в рабочем диапазоне частот антенны, дБ; fгрi – граничная (нижняя или верхняя) частота рабочего диапазона частот антенны, i = 1, 2; Ci – коэффициент, характеризующий скорость снижения коэффициента усиления антенны за пределами границы, определяемой частотой fгрi, дБ/дек; Di – постоянная, определяющая изменение коэффициента усиления антенны на границах ее рабочего диапазона частот, дБ. Постоянные Ci и Di в уравнении (10.6) должны определяться для конкретного типа антенны на основе измерений ДНА на частотах, которые являются нерабочими для данного типа антенны. В качестве примера можно привести модели бортовых самолетных антенн: штыревой ножевидной антенны для системы связи с диапазоном рабочих частот 118…135 МГц и рамочной антенны для системы навигации с рабочей частотой 115.4 МГц [39]. По результатам измерений и анализа характеристик антенн в диапазоне ВЧ (2…30 МГц) для частот f < fгр1 были предложены следующие модели для коэффициентов усиления антенн: - для штыревой антенны Gшт(f) = G0 + 25 lg (f / fгр1); - для рамочной антенны Gрам(f) = G0 + 50 lg (f / fгр1). Выражение (10.6) по существу является описанием частотной характеристики антенны за пределами рабочего диапазона частот антенны. При отсутствии экспериментальных данных реальную частотную характеристику антенны можно заменить характеристикой прямоугольной формы, полагая C1 = C2 = 0 и D1 = D2 = D. Значение D можно взять из таблицы 10.1, где указано также ожидаемое расширение диаграммы направленности в горизонтальной и в вертикальной плоскостях на нерабочих частотах в зависимости от усиления антенны в диапазоне ее рабочих частот. Формула (10.6) и данные табл. 10.1 определяют параметры главного лепестка основных сечений ДНА в области нерабочих частот антенны. Построение трехмерной ДНА в этой области может быть выполнено так, как и в рабочей области, но с учетом новых значений коэффициента усиления и ширины ДНА в горизонтальной и вертикальной плоскости. Таблица 10.1 Параметры диаграмм направленности за пределами диапазона рабочих частот антенн.
Примечание. φ0 и θ0 – соответственно, ширина ДНА в горизонтальной и в вертикальной плоскости на уровне 3дБ в диапазоне рабочих частот антенны Что касается области боковых лепестков, то, как показывают многочисленные измерения антенн с высокой направленностью, основные характеристики усиления в этой области не изменяются, и модель ДНА в области боковых лепестков на нерабочих частотах может быть взята такой же, как и в области рабочих частот.
Детерминированное описание ДНА не может учесть влияния всех факторов на параметры и форму диаграммы направленности, особенно в области боковых и задних лепестков. Изменчивость характеристик антенны в этой области лучше всего может быть выражена посредством их статистического описания. Экспериментальные исследования диаграмм направленности антенн, обладающих узким главным лепестком и высоким коэффициентом усиления по главному лепестку, показали, что коэффициент усиления в области боковых и задних лепестков, выраженный в децибелах, может быть описан нормальным законом распределения. Интегральная функция распределения коэффициента усиления имеет вид: 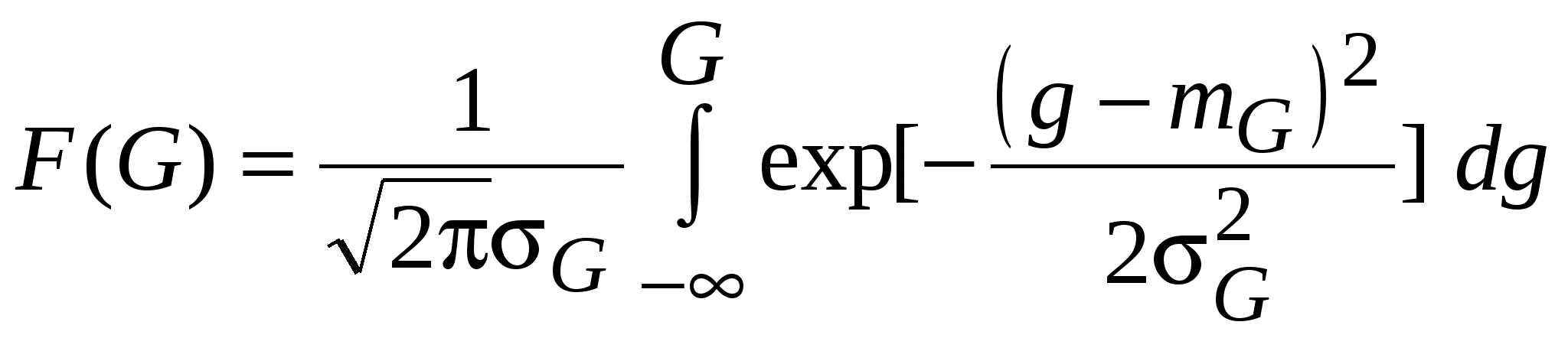 ,где mG и G – соответственно, математическое ожидание (среднее) и среднеквадратическое отклонение усиления в области боковых и задних лепестков ДНА, дБ. Параметры распределения mG и G получают посредством статистической обработки результатов измерений ДНА в области боковых и задних лепестков. Статистическое описание ДНА отличается высокой стабильностью своей формы и параметров, как в рабочем диапазоне частот антенны, так и вне его. На статистическое описание и значения его параметров мало влияет поляризация сигналов и окружающие объекты. Структура боковых лепестков изменяется, однако распределение вероятностей и значения его параметров сохраняются. Отражения от окружающих объектов, размещенных вблизи антенны, оказывают некоторое влияние на параметр mG, которое приводит к небольшому его увеличению. В целом это влияние зависит от размеров окружающих элементов и от начального (т. е. без окружающих элементов) медианного усиления антенны. Чем ниже начальное медианное усиление антенны, тем больше это влияние. Описание бокового усиления антенн нормальным законом распределения используется не только для антенн с высоким коэффициентом усиления по главному лепестку, но и для других типов антенн. Для ориентировочных и оперативных расчетов при прогнозировании уровней помех можно использовать данные, приведенные в табл. 10.2 [16], где представлены параметры распределений бокового усиления в зависимости от усиления по главному лепестку. Статистическое описание ДНА в области боковых и задних лепестков обычно применяется в методиках оценки ЭМС, основанных на использовании имитационного статистического моделирования. Учитывая, что в области главного лепестка ДНА на рабочих частотах для одного и того же типа антенн имеет место технологический разброс коэффициента усиления антенны, при имитационном моделировании нормальный закон может быть использован и для описания максимального усиления по главному лепестку. Параметрами закона являются mG = G0, G = 2 дБ. Таблица 10.2 Параметры функции F(G) для области бокового усиления
Статистика измерений усиления в области боковых и задних лепестков ДНА дает материал для выбора постоянных значений коэффициента усиления при детерминированном описании диаграмм направленности в этих областях.
Потери при передаче сигнала от передатчика к антенне или от антенны к входу радиоприемного устройства (РПУ) складываются из потерь непосредственно в антенно-фидерном тракте (АФТ) и потерь рассогласования АФТ с антенной или входом РПУ. Для АФТ обычно известна марка кабеля или волновода, используемого для передачи поступающих в него сигналов, и, следовательно, известны погонные потери в тракте (f) [дБ/м], которые в общем случае зависят от частоты. Потери в АФТ легко определить, используя уравнение: LАФТ(f) = lАФТ (f), где LАФТ(f) – потери в АФТ на частоте f, дБ; lАФТ – длина кабеля или волновода АФТ, м. Потери рассогласования имеют место, если сопротивление нагрузки антенно-фидерного тракта (входное сопротивление приемника или сопротивление антенны) не согласовано с волновым сопротивлением тракта. Добиться точного согласования нагрузки с волновым сопротивлением кабеля во всем диапазоне рабочих частот практически невозможно. Рассогласование приводит к тому, что часть мощности, передаваемой по тракту, не поступает в нагрузку, отражаясь от нее. В качестве характеристики, определяющей степень согласования АФТ с нагрузкой, используется коэффициент стоячей волны по напряжению (КСВН). Обозначим его . По определению =  ,где Umax – значение напряжения в максимуме стоячей волны; Umin – значение напряжения в минимуме стоячей волны. Учитывая, что  ,где  ,  – максимальные значения падающей и отраженной волн, соответственно;  – модуль коэффициента отражения,можно установить связь между КСВН и коэффициентом отражения ||:  или  При рассогласовании линии передачи (АФТ) с нагрузкой мощность P, поступающая в нагрузку: P = P+ – P– = P+(1 – P– / P+), где P+ – мощность, подводимая к нагрузке; P– – мощность, отраженная от нагрузки. Так как  , то P = P+(1–||2) (10.7)  Таким образом, множитель  определяет долю мощности от полной мощности в линии передачи, которая поступает в нагрузку. Соответственно, потери мощности, выраженные в децибелах и вызванные рассогласованием, можно оценить как Q = 10 lg (q) = 10 lg  (10.8)В полосе рабочих частот антенны обычно известно максимальное значение КСВН, что позволяет использовать формулу (10.8) для оценки максимальных потерь сигналов в этой полосе частот. Для частот за пределами рабочего диапазона потери на рассогласование в общем случае могут быть получены на основании измерений коэффициента отражения в АФТ. В этом случае, как следует из (10.7) q = 1 – |Γ|2 или в децибелах Q = 10 lg (q). При отсутствии данных о коэффициенте отражения для ситуации наихудшего случая может быть сделано допущение, которое в определенной степени подтверждается экспериментом [40], что для антенн с относительно невысоким коэффициентом усиления рассогласование на частотах выше верхней граничной частоты остается не хуже, чем в рабочем диапазоне частот. Для частот ниже нижней граничной частоты fгр1 рабочего диапазона Q = 20lg (f/ fгр1), дБ
В дальней зоне излучения фронт электромагнитной волны становится плоским, а плоская волна является поляризованной. Поляризация электромагнитной волны определяется траекторией и направлением движения во времени конца вектора напряженности электрического поля Е в фиксированной плоскости, перпендикулярной направлению распространения электромагнитной волны, если смотреть на плоскость в направлении распространения. В общем случае электромагнитная волна для гармонического излучения является эллиптически поляризованной. Если, как это представлено на рис. 10.6, электромагнитная волна распространяется вдоль оси z, а плоскость x0y перпендикулярна направлению распространения, то конец вектора Е в этой плоскости относительно точки 0 будет описывать эллипс. В зависимости от направления вращения вектора Е различают правостороннюю и левостороннюю эллиптические поляризации. Если вектор Е вращается по часовой стрелке, то имеет место правосторонняя эллиптическая поляризация. Если вектор Е вращается против часовой стрелки, то имеет место левосторонняя эллиптическая поляризация. Круговая и линейная поляризации являются частными случаями эллиптической поляризации. Ф 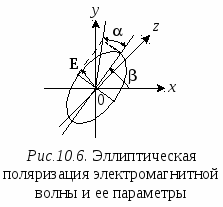 орма эллипса описывается коэффициентом эллиптичности r, где  ,которому приписывают знак «плюс» при правосторонней поляризации и знак «минус» при левосторонней поляризации (–1 ≤ r ≤ 1). Можно ввести угол эллиптичности α = arctg(r), (–π/4 ≤ α ≤ π/4), и угол ориентации β между осью 0x и большой полуосью эллипса (0 ≤ β ≤ π). Углы α и β полностью определяют состояние поляризации. Состояния поляризации можно отобразить точками на сфере, которую принято называть сферой Пуанкаре, если в качестве долготы и широты точки, определяющей состояние поляризации, взять углы 2β и 2α, соответственно (рис. 10.7). Каждому состоянию поляризации соответствует точка на сфере Пуанкаре, и, обратно, каждой точке на сфере Пуанкаре соответствует определенное состояние поляризации. Для круговой поляризации значение β не определено, и ей соответствуют полюса сферы, в которых не определена долгота. Точки, расположенные на экваторе, соответствуют разным видам линейной поляризации, а все остальные точки сферы отображают различные виды эллиптической поляризации. Северная полусфера представляет правостороннюю поляризацию, а южная – левостороннюю. Параметры, определяющие форму и положение эллипса поляризации, могут иметь определения, отличающиеся от приведенных выше. Например, в стандарте США [42] коэффициент эллиптичности r определяется как отношение большой оси эллипса поляризации к малой, а угол эллиптичности α как минус arcctg(r). Коэффициент эллиптичности по-прежнему имеет знак плюс для правосторонней и минус для левосторонней поляризации. Это приводит к тому, что коэффициент эллиптичности изменяется в интервале от единицы до бесконечности с соответствующим знаком, а полусферы сферы Пуанкаре, представляющие правостороннюю и левостороннюю поляризации, м 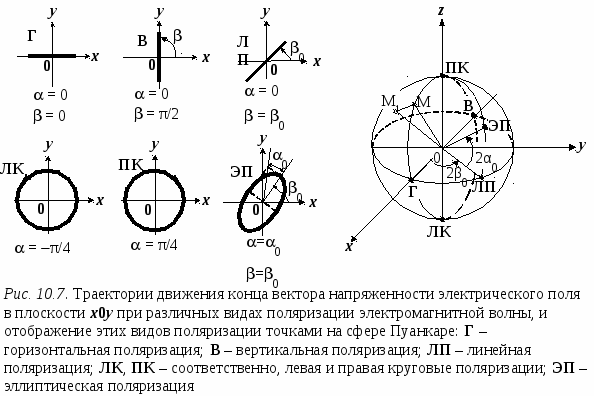 еняются местами. Если на сфере Пуанкаре рассмотреть две точки М и М1, одна из которых соответствует поляризационному состоянию приемной антенны, а другая поляризации падающей электромагнитной волны, то э.д.с. на зажимах антенны можно рассчитать, используя выражение: e = Ehд cos(  MM1/2), (10.9)где e – э.д.с. на зажимах антенны, В; E – напряженность поля в месте размещения антенны, В/м; hд – действующая высота антенны, м; MM1 – угол между точками на сфере Пуанкаре, определяющими поляризационные состояния антенны и приходящей электромагнитной волныОслабление из-за несовпадения поляризаций поступающего сигнала и приемной антенны, выраженное в децибелах, имеет вид: = 20 lg (cos( MM1/2)), (10.10)Если MM1 = 180, то, как следует из (10.9) и (10.10), e = 0 и = – . Поляризации такого вида называются ортогональными. Ортогональными, в частности, являются горизонтальная и вертикальная поляризации, левая и правая круговые поляризации и, вообще, две любые поляризации, соответствующие точкам на сфере Пуанкаре, которые лежат на противоположных концах диаметра сферы. Таким образом, теоретически сигналы, имеющие ортогональную поляризацию, не создают друг другу помех, поскольку э.д.с., возникающая на выходах антенн, не предназначенных для приема этих сигналов, будет равна нулю, или, что то же самое, антенны обеспечивают бесконечное подавление ортогональных сигналов.Однако на практике идеально ортогональных сигналов не существует. Взаимное расположение антенн, условия распространения и сама среда распространения приводят к тому, что (MM1/2) становится меньше 90. В результате вместо бесконечного ослабления ортогонального сигнала в антенне происходит лишь частичное его подавление. Так, например, если вместо 90 (MM1/2) = 85, то вместо бесконечного ослабления = 20 lg (cos(85)) = –20 дБ. Учитывая это обстоятельство, при оценке ЭМС РЭС, использующих ортогональные сигналы, ослабление таких сигналов всегда берут конечное, чаще всего в интервале –16…–25 дБ, в зависимости от коэффициента усиления антенн и вида радиослужбы. Например, станции фиксированной службы или базовые станций наземной подвижной службы часто работают с сигналами, которые являются ортогонально поляризованными по отношению к сигналам телевизионного (ТВ) вещания. Первые используют вертикальную поляризацию, а телевидение использует горизонтальную поляризацию. При оценке помех, создаваемых такими станциями приему ТВ вещания, Рекомендация МСЭ-Р SM.851-1 [41] предлагает использовать значение ослабления мешающих сигналов –16 дБ для 50 % мест обслуживания и значение –10 дБ для 90 % мест обслуживания станции ТВ вещания. Для базовых станций с сигналами, имеющими вертикальную поляризацию, подавление антеннами излучений станций радиовещания, имеющих горизонтальную поляризацию, рекомендовано брать –18 дБ. В общем случае ослабление ортогональных сигналов при оценке ЭМС выбирают либо, следуя рекомендациям МСЭ, либо, исходя из результатов практических измерений, либо на основании теоретических оценок при принятых гипотезах о нарушении ортогональности. Если информация о подавлении ортогональной поляризации отсутствует, можно использовать данные, приведенные в табл.10.3 для наиболее часто используемых на практике видов поляризаций. Данные представлены в децибелах. Таблица 10.3 Ослабление мешающих сигналов при несовпадении поляризации с приемной антенной
Можно заметить, что если одна из антенн, например источника помехи, имеет круговую поляризацию, а другая, например приемника, имеет линейную поляризацию, то ослабление мешающего сигнала приемной антенной из-за различия поляризаций, представленное в табл. 10.3, получено непосредственно из выражения (10.10). Действительно, в этом случае MM1 = 90 и = 20 lg [cos(45)] = –10 lg (2) = –3дБ Приведенная оценка потерь на рассогласование поляризаций относится к главному лепестку ДНА и рабочему диапазону частот антенны. В области боковых лепестков, особенно у направленных антенн, поляризация может быть совершенно иной, чем поляризация по главному лепестку. На практике потери на рассогласование поляризаций в области боковых лепестков в диапазоне рабочих частот и за его пределами не рассматривают, поскольку уровень боковых лепестков, используемый в модели ДНА, обычно связан со статистическими параметрами усиления антенны по боковым лепесткам, которые, как указывалось выше, слабо зависят от частоты и поляризации сигналов. Потери на рассогласование поляризаций не рассматривают также в ближней зоне, где ДНА еще не сформировалась и связь между магнитной и электрической составляющими электромагнитной волны носит сложный характер.
Оценка взаимодействия антенн, размещаемых на одном объекте, носит специфический характер, поскольку ситуация требует расчета взаимодействия между близко расположенными антеннами, в том числе между антеннами, находящимися в ближней зоне друг друга. Это определяет специфику анализа ЭМС радиоэлектронных средств, установленных на одном объекте, среди других проблем ЭМС РЭС [78]. В ближней зоне коэффициент усиления антенны в заданном направлении зависит от расстояния от антенны. Получить теоретические зависимости коэффициента усиления от расстояния от антенны удается только в частных случаях для относительно простых антенн, таких например, как рупорная антенна, антенна в виде открытого волновода [43] или полуволновой вибратор. Получаемые результаты обычно дают зависимость максимального усиления антенны в свободном пространстве от расстояния до антенны. Использовать эти результаты можно только в ограниченном числе ситуаций. Кроме того, близко расположенные антенны могут влиять друг на друга. При оценке уровней мешающих сигналов в приемной антенне, которая близко расположена по отношению к передающей антенне, наиболее часто используют параметр, называемый коэффициентом связи антенн. Под коэффициентом связи антенн понимают отношение мощности, подведенной к антенне передатчика, к мощности, полученной на нагрузке приемной антенны. Коэффициент связи обычно выражают в децибелах. Иногда под коэффициентом связи антенн понимают выраженное в децибелах отношение мощности, полученной на нагрузке приемной антенны, к мощности, подведенной к антенне передатчика. Этот коэффициент связи отличается от приведенного выше только знаком. Для оценки коэффициента связи используют следующие подходы: 1. Оценка коэффициента связи между антеннами посредством решения электродинамической задачи для интересующего размещения антенн. Задача обычно описывается интегральным, дифференциальным или интегро-дифференциальным уравнением, связывающим токи, распределенные по элементам передающей антенны, с полем излучения и токами, наведенными этим полем на окружающие элементы, в том числе на приемные антенны. Каждый метод описания имеет определенные практические ограничения, требует подробной информации о геометрии антенн и элементов конструкций, которые окружают антенны. 2. Использование статистических данных о результатах измерений коэффициентов связи между антеннами в ситуациях, аналогичных рассматриваемой (если такие данные имеются). 3. Использование приближенных формул для оценки коэффициентов связи между близко расположенными антеннами определенного вида. Т 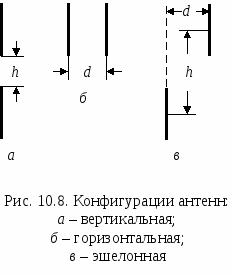 ак для антенн, представляющих собой ненаправленные в горизонтальной плоскости вертикальные диполи, в свободном пространстве для расстояний между антеннами d < 6 м связь между антеннами можно оценить, используя следующие приближенные формулы (рис. 10.8) [44]:
Lv = 28 + 40 lg (h/λ) , дБ
Lh = 22 + 20 lg (d/λ) – (GT + GR) , дБ
Ll = Lh + (Lv– Lh)  где Lv – вертикальная развязка, дБ; Lh – горизонтальная развязка, дБ; Ll – развязка уступа, дБ; h – разнос антенн по вертикали; d – горизонтальный разнос антенн; λ – длина волны; arctg(x) в радианах; GT, GR – эффективное усиление антенн, dBi. Эффективное усиление антенн в ближней зоне близко к 0 dBi. Иногда развязка между антеннами в ближней зоне оценивается как L = Lсв + (5…7), дБ, где Lсв – ослабление электромагнитной волны при распространении в свободном пространстве, дБ. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||