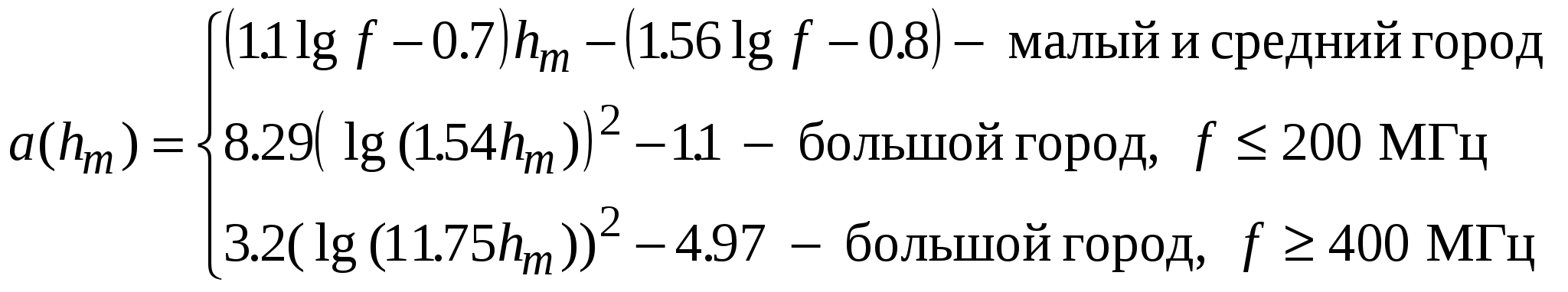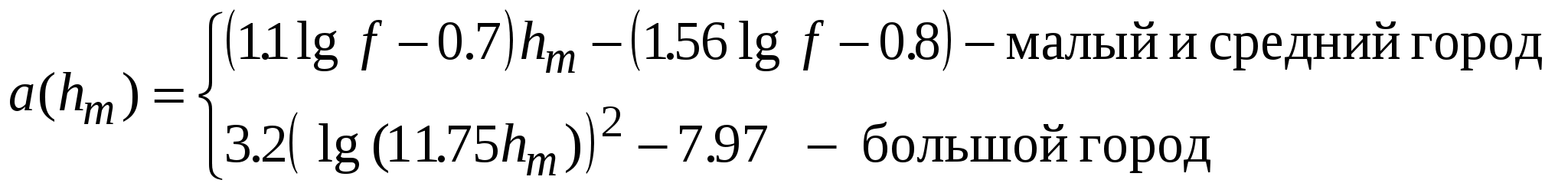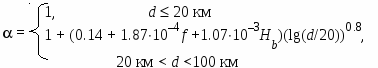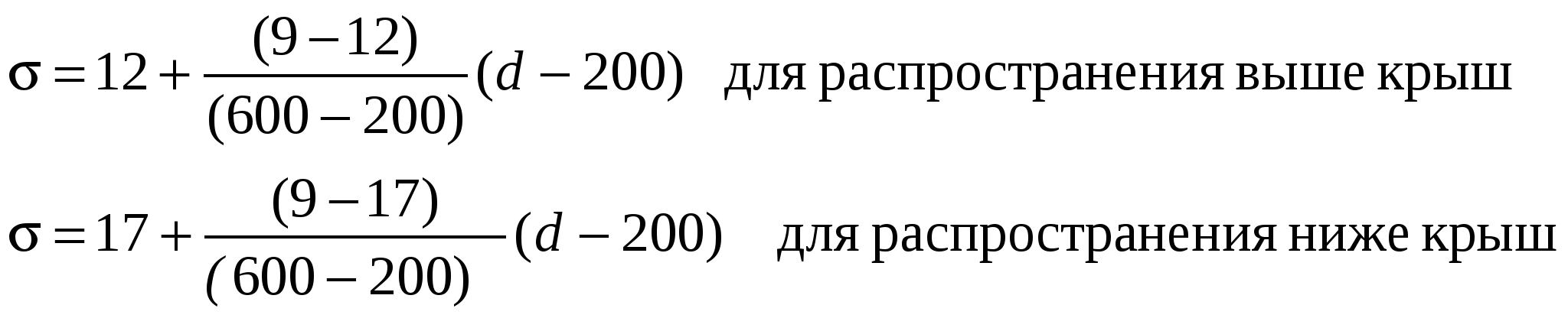Уч пособие ЭМС_2. Е. М. Виноградов
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
Графические моделиКак отмечено выше, графические модели могут иметь разный вид. Рассмотрим в общих чертах две графические модели, которые рекомендованы Международным союзом электросвязи (МСЭ) для оценки напряженности поля, создаваемой излучениями радиопередатчиков в диапазонах частот 10 кГц…30 МГц и 30…3000 МГц. Модели относятся к разным диапазонам частот и разным видам распространения электромагнитных волн и представлены в Рекомендациях МСЭ-Р P.368 и P.1546 [46], соответственно. МСЭ-Р Рекомендация P.368-7[45]. Рекомендация позволяет провести оценку напряженности поля и потерь при распространении электромагнитных колебаний земной волной в диапазоне частот от 10 кГц до 30 МГц. Предлагаемая модель, по существу, является детерминистской, поскольку представленные в рекомендации кривые являются теоретическими расчетными кривыми, полученными при следующих условиях: – распространение радиоволн происходит над гладкой, однородной сферической Землей; – передающая и приемная антенны находятся на поверхности земли; – излучающий элемент – короткий вертикальный несимметричный вибратор; – излучаемая мощность 1кВт. Сигналы с вертикальной поляризацией, распространяющиеся земной волной, испытывают значительно меньшее ослабление, чем сигналы с горизонтальной поляризацией. Рекомендация содержит набор семейств параметрических кривых, которые дают значение вертикальной составляющей поля излучения и имеют вид: Е = (d), (11.1) где Е – напряженность поля, создаваемая коротким вертикальным несимметричным вибратором, расположенным на поверхности земли и излучающим мощность 1 кВт, дБ(мкВ/м); d – расстояние от излучателя до точки приема, км. Параметром кривых, представленных в каждом семействе, является частота. Параметрами семейств кривых являются электрические параметры земной поверхности: удельная проводимость почвы σ [С/м] и относительная диэлектрическая проницаемость почвы ε. Н 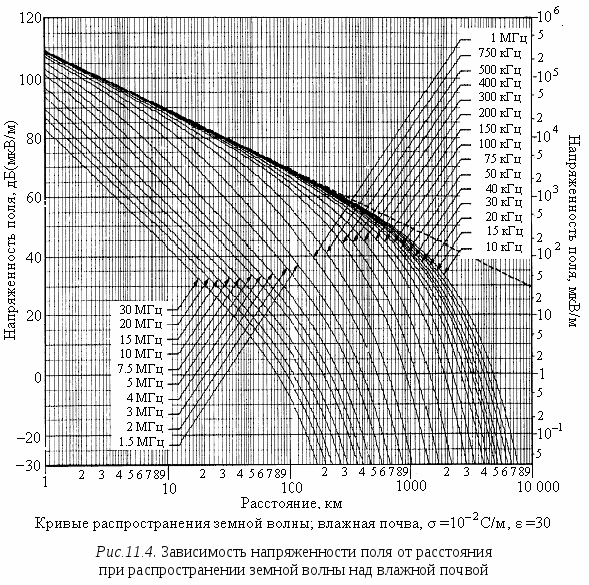 а рис. 11.4 представлено семейство кривых для определенных значений удельной проводимости и относительной диэлектрической проницаемости почвы. Если частота сигнала не совпадает ни с одной из частот, для которых построены кривые, то напряженность поля на этой частоте определяется посредством линейной интерполяции напряженности поля между кривыми для ближайших частот, между которыми лежит интересующая частота. Если напряженность поля определена из приведенных кривых, то базовые потери при распространения земной волной на трассе протяженностью d, км, можно получить из уравнения: Lb = 142+20 lg (f) – E, (11.2) где Lb – основные (базовые) потери на трассе распространения, дБ; f – частота сигнала, МГц; E – напряженность поля на частоте f, дБ(мкВ/м), на расстоянии d, км, полученная с использованием кривых МСЭ-Р Рек. P.368-7. Оценка потерь на трассе распространения на основе Рекомендации P.368 производится только для земной волны, когда отражения от ионосферы незначительны. Поскольку кривые, представленные в Рекомендации, относятся к однородным трассам, в приложении II к Рекомендации приводится методика использования этих кривых для смешанных трасс. Для прогнозирования напряженности поля в системах «точка область» МСЭ разработал универсальную графическую модель, реализованную в рекомендации P.1546. Модель построена аппроксимацией между кривыми ряда других графических моделей и предназначена для использования в системах радиовещания, системах наземной и морской подвижных радиослужб и некоторых фиксированных служб, где используются системы связи типа «точка много точек». МСЭ-Р Рекомендация P.1546-1. В рекомендации представлен набор семейств параметрических кривых вида E = (d), где E – напряженность поля, создаваемая передатчиком с эффективной излучаемой мощностью (ЭИМ) 1кВт на расстоянии d, км, от передатчика, дБ(мкВ/м). Под эффективной излучаемой мощностью понимается произведение мощности, подведенной к антенне передатчика, на коэффициент усиления антенны относительно полуволнового диполя. Диапазон рабочих частот, в котором может быть использована рекомендация, составляет 30…3000 МГц, а диапазон расстояний 1…1000 км. Модель является статистической, поскольку представленные в ней кривые основаны на статистическом анализе экспериментальных данных для наземных трасс в зонах с умеренным климатом (Европа и Северная Америка) и данных для средних климатических условий по температуре, содержащих холодное и теплое моря (Северное и Средиземное моря). Н 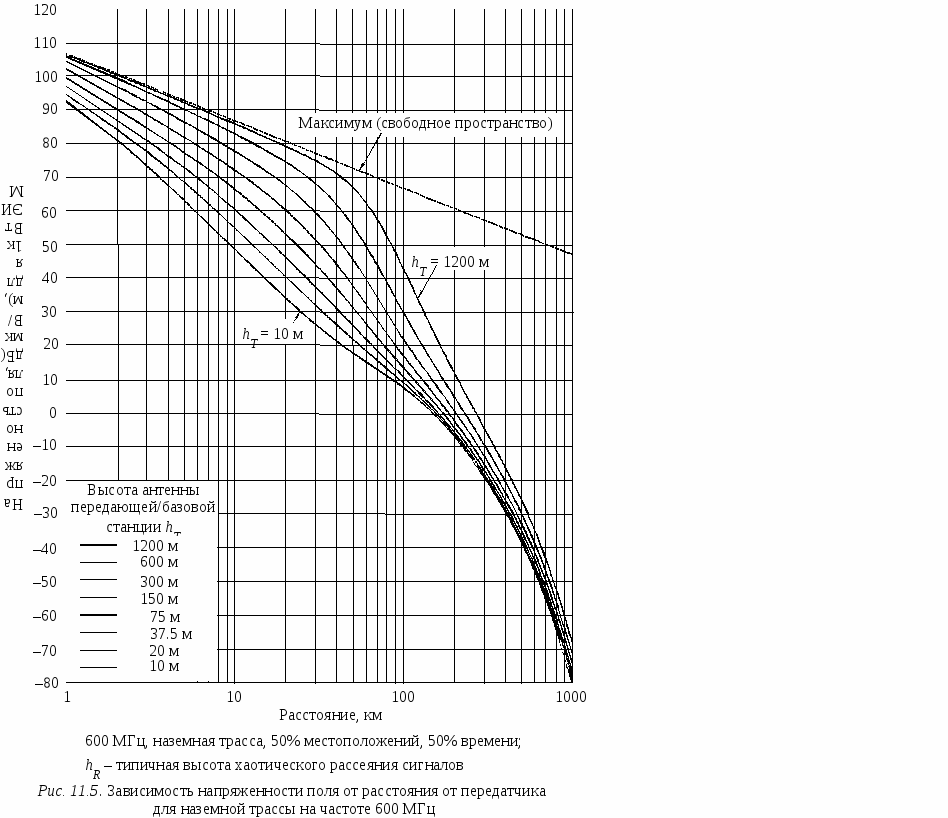 а рис. 11.5 представлено одно семейство кривых из рассматриваемой Рекомендации. В каждом семействе параметром кривых является высота передающей антенны hT (в оригинале h1). Высота передающей антенны, которая используется при расчетах, зависит от типа и длины трассы. Так для морских трасс в качестве высоты передающей антенны берется физическая высота антенны над поверхностью моря. Для наземных трасс протяженностью более 15 км используется эффективная высота антенны. В рекомендации эффективная высота антенны определена как разность между физической высотой антенны и средней высотой местности в диапазоне расстояний от передатчика от 3 км до 15 км в направлении на приемную антенну. Для ее вычисления необходима информация о рельефе местности, которую обычно получают из цифровых карт местности, используя подходящие геоинформационные системы. Для наземных трасс короче 15 км эффективную высоту передающей антенны рассчитывают также с использованием информации о рельефе местности, но применяя другой метод вычисления, представленный в Рекомендации. Имеются определенные особенности использования кривых, связанные с высотой приемной антенны. Для морских трасс значение высоты приемной антенны взято 10 м (hR= 10 м). Именно для такой высоты приемной антенны построены кривые зависимости напряженности поля от расстояния для трасс, проходящих над морем. Для сухопутных трасс кривые напряженности поля относятся к высоте приемной антенны, соответствующей типичной высоте хаотического рассеяния радиосигналов покрытием земли, окружающим приемную антенну. Типичные высоты хаотического рассеяния радиосигналов представлены значениями: 10 м – для пригородной зоны и сельской местности, 20 м – для городской зоны, и 30 м для городской зоны с плотной (высотной) застройкой. Минимальное значение высоты хаотического рассеяния определено значением 10 м. В зависимости от истинного положения приемной антенны по отношению к предполагаемой высоте хаотического рассеяния применяются поправки к значениям напряженности поля, полученным непосредственно из приведенных кривых. Семейства кривых различаются значениями параметров, которые отделяют одно семейство от другого и относятся ко всем кривым семейства. В число этих параметров входят: частота излучения передатчика, вид трассы (наземная, морская, холодное море, теплое море), а также параметры, характеризующие изменчивость напряженности поля во времени и пространстве. Изменчивость определяется процентом мест, в которых в пределах любой площадки размером 200 м × 200 м в течение определенного процента времени значение напряженности поля будет не ниже, чем значение, полученное из приведенных кривых. Для всех семейств кривых процент мест взят равным 50 %, а процент времени для разных семейств имеет значения 50 %, 10 % и 1 %. Применение предлагаемых графиков для вычислений напряженности поля является достаточно сложной процедурой. Редко бывает так, чтобы и частота передатчика, и высота передающей антенн, и другие параметры, определяющие кривые, в точности соответствовали параметрам решаемой задачи. Поэтому рекомендация содержит описание ряда процедур, связанных с интерполяцией или экстраполяцией значений напряженности поля, получаемых из приведенных графиков и направленных на получение значений, соответствующих поставленной задаче, включая смешанные трассы. Если на интересующем расстоянии напряженность поля получена, то можно рассчитать эквивалентные базовые потери Lb = 139 + 20 lg (f) E, (11.3) где Lb – базовые (основные) потери передачи, дБ; f – частота, МГц; E – напряженность поля, дБ(мкВ/м), для 1кВт ЭИМ. Представленное краткое описание двух графических моделей показывает трудности, связанные с их практическим применением. Во-первых, имеются определенные проблемы перевода графиков в цифровую форму, чтобы выполнять расчеты с использованием ЭВМ. Во-вторых, графические модели не могут быть представлены только графиками. Нужно еще описание методики их использования в ситуациях, отличных от тех, для которых построены графики. Графические модели, используемые для решения задач частотно-территориального планирования и оценки ЭМС, обычно представляют зависимость E(d).
Как уже отмечалось, уровень сигнала в точке приема является случайной величиной, испытывающей медленные и быстрые флюктуации, величина которых зависит от ситуации. Аналитические модели, оценивают медианное значение потерь на трассах распространения. Аналитические модели для оценки потерь радиосигналов на трассах распространения могут иметь разный вид. В настоящее время существует достаточно много аналитических моделей для оценки потерь в различных ситуациях. Кратко остановимся на некоторых, достаточно часто используемых моделях, а именно: модели потерь в свободном пространстве, модифицированной модели Хата и модели Уолфиша-Икегами. Модель потерь в свободном пространстве. Среди моделей, используемых для оценки потерь при распространении радиоволн, важную роль играет модель оценки потерь при распространении в свободном пространстве. Во-первых, формула для оценки потерь в свободном пространстве выводится теоретически и потери, определяемые ею, являются неслучайной величиной. Во-вторых, медианные потери для других сред распространения, отличных от свободного пространства, не могут быть меньше потерь в свободном пространстве. В этом смысле формула потерь в свободном пространстве может использоваться в качестве одного из критериев применимости других математических моделей в конкретных ситуациях, а именно: если медианные потери, рассчитанные при данных условиях меньше, чем потери в свободном пространстве, то использованная модель не применима к данной ситуации, поскольку дает недостоверные результаты. Модель для оценки потерь в свободном пространстве имеет и самостоятельное значение. Она используется в ситуациях, когда влиянием других факторов (влиянием подстилающей поверхности, тропосферы, ионосферы и т. п.) на потери распространения, кроме расширения фронта волны, можно пренебречь. Оценка, полученная на основе модели распространения в свободном пространстве, используется и тогда, когда другие модели дают значение медианных потерь меньше, чем потери в свободном пространстве. В свободном пространстве ослабление уровня сигнала происходит только за счет расширения фронта волны. Основные потери в свободном пространстве описываются следующим выражением: Lсв = 32.45+20 lg d+ 20 lg f, (11.4) где Lсв – потери при распространении в свободном пространстве, дБ; d – расстояние от антенны передатчика (излучателя) до рассматриваемой точки, км; f – частота сигнала, МГц. Формулу (11.4) можно получить следующим образом. Поскольку потери рассматриваются между изотропными антеннами то плотность потока мощности W в свободном пространстве, создаваемая передатчиком с мощностью PT и изотропной антенной, на расстоянии d W = PT/(4d 2) Мощность сигнала S, принимаемого антенной с эффективной площадью Аэф S= WAэф= PTАэф/(4d 2) Учитывая, что эффективная площадь изотропной антенны Аэф = 2/(4), где – длина волны, принимаемого сигнала, и = c/f, где с – скорость света в свободном пространстве, а f – частота сигнала, получим S = PTc2/(4df)2 Обозначим lсв = (4d f)2/c2 – множитель ослабление сигнала в свободном пространстве. Выражая lсв в децибелах, с – в км/с, d – в км и f – в МГц, получим Lсв = 10 lg (lсв) = 20 lg (4d f/c) = 20 lg (4d f·106/3·105) = 32.45+20 lg d+20 lg f В дальнейшем, если не оговорено особо, в моделях, используемых для оценки потерь на трассах распространения, расстояние будет всегда выражаться в километрах, а частота в мегагерцах. Модель потерь в свободном пространстве является детерминистской моделью. Ее достоинством является очень простой вид, хотя область применения ограничена ситуациями, в которых влиянием окружения на распространение радиоволн можно пренебречь. В некоторых случаях модель потерь в свободном пространстве используется как элемент более сложной модели, учитывающей влияние окружения на потери при распространении радиоволн (например, поглощение растительностью или газами, дифракцию, отражения и т. п.). Большой простотой отличается статистическая модель Эгли. Модель базируется на результатах измерений на трассах, преобразованных в математическую модель. Модель Эгли[47]. Одна из известных статистических моделей для предсказания средних потерь. Является сильно упрощенной моделью, которая предполагает гладкую холмистую поверхность со средней высотой неровностей примерно 15 м. Согласно Эгли средние потери распространения вычисляются по формуле: 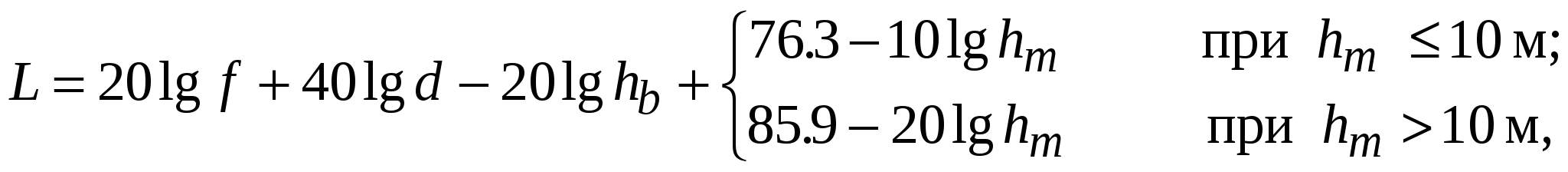 (11.5) (11.5)где L – средние (медианные) потери распространения, дБ; f – частота, МГц; d – расстояние от передатчика до точки приема, км; hb, hm – эффективные высоты антенн базовой и мобильной станций соответственно, м. Диапазон частот, в котором может быть использована формула (11.5), составляет 40…1000 МГц. Широкое использование новых радиотехнологий в полосах частот, лежащих в диапазонах ОВЧ и УВЧ, потребовало разработки математических моделей, позволяющих выполнить оценку потерь в этих диапазонах частот для различных условий распространения радиоволн. По результатам измерений в районе Токио была построена модель, получившая название модель Окумура (Okumura). Методика расчета, положенная в основу модели, представлена в работе [48]. В методике используются графики, полученные путем статистической обработки результатов измерений, которые позволяют определить медианную напряженность поля для городских областей, а также выполнить подстройку используемой модели по степени урбанизации рассматриваемой области и по некоторым другим особенностям трассы распространения: наклону земной поверхности, степени ее неровности, общей ориентации улиц в зоне обслуживания и т. п. По степени урбанизации окружения мобильной станции в методике Окумура выделены три области: Открытая (сельская) область – область рассматривается как открытая, если в окрестности приемной станции (например, мобильного средства) на расстояниях 300…400 метров отсутствуют препятствия в направлении передающей (например, базовой) станции. Пригородная область – область, в которой в окрестности приемной станции имеются препятствия, но плотность их мала. Городская область – город с высокими зданиями и домами высотой не менее двух этажей. Кроме того, городская область делится на большой и средний город, а открытая область – на открытую и «квазиоткрытую» (область, которая является средней между открытой и пригородной). Все определения областей носят качественный характер, что представляет определенные неудобства для их использования. Поскольку зависимости напряженности поля от расстояния и корректирующие коэффициенты в модели Окумура представлены в графической форме, то использование такого материала для практических расчетов, особенно в задачах ЭМС, представляет определенные трудности. М. Хата (M. Hata) преобразовал кривые Окумура в уравнения, получившие название модели Хата. В классической модели Хата [49] выполнен расчет медианных базовых потерь, а не напряженности поля. Уравнения ограничены трассами длиной от 1 до 20 км. Кроме того, было ограничено применение некоторых корректирующих коэффициентов. Модель получила широкое распространение, особенно для проектирования систем подвижной радиосвязи. Была расширена область ее применения, и в настоящее время используется несколько вариантов, различающихся своими возможностями. Классическая модель Хата [49].Область применения: – диапазон частот f = 150…1500 МГц; – высота подъема антенны базовой станции hb = 30…200 м; – высота подъема антенны мобильной станции hm = 1…10 м; – длина трассы d = 1…20 км. Основные расчетные формулы представлены в табл. 11.1. Таблица 11.1 Расчетные соотношения, используемые в классической модели Хата
Модель COST 231 Хата. Область применения: – диапазон частот f = 1500…2000 МГц; – остальные параметры совпадают с классической моделью Хата. Основные расчетные формулы представлены в табл. 11.2. Таблица 11.2 Расчетные соотношения, используемые в модели COST 231 Хата
Модифицированная модель Хата [50]. Модель имеет более широкие границы применения, чем модели, рассмотренные выше: – диапазон частот f = 30…3000 МГц; – высота подъема антенн базовой и мобильной станций hb, hm = 1…200м; – длина трассы d = 0.1…100 км. Если высота одной из антенн менее 1 м, то в формулах Хата следует использовать значение 1 м. Расчетные соотношения для оценки средних потерь на основе модифицированной модели Хата приведены в табл. 11.3. Таблица 11.3 Расчетные соотношения, используемые в модифицированной модели Хата
Примечание. В таблице использованы обозначения: f – частота, МГц; Hm= min(hb, hm), м; Hb= max(hb, hm), м; d – расстояние, км. Как видно из табл. 11.3 модель дополнена оценкой потерь в зоне, близкой к радиопередатчику, граница которой определена расстоянием менее 40 м, и оценкой потерь в промежуточной зоне, которая простирается от 40 м до 100 м. В близкой зоне потери распространения оцениваются значением потерь в свободном пространстве. В промежуточной зоне – линейной интерполяцией (при логарифмической шкале дальностей) потерь в свободном пространстве между точками 40 м и 100 м. Так как потери L на трассе распространения являются случайной величиной, которая считается распределенной по нормальному закону (если L выражено в дБ), в табл. 11.4 представлены ожидаемые значения среднеквадратического отклонения (СКО) потерь распространения, которые зависят только от расстояния и положения антенны базовой станции и не зависят от частоты. Таблица 11.4 Среднеквадратическое отклонение (СКО) потерь на трассах распространения
В модели Хата окружение абонентской станции оценивается на качественном уровне. Модель Уолфиша-Икегами, разработанная для использования в городских и пригородных условиях, требует более подробной информации о структуре окружения. При оценке потерь на трассе распространения модель рассматривает поступление сигнала в точку приема по разным лучам. Тем не менее, она остается статистической, поскольку в ней не рассматриваются топографические данные зданий, а используются только характерные (типичные или средние) значения параметров окружения базовой станции. Дифракционная модель Уолфиша – Икегами [51]. Модель предназначена для оценки потерь на трассах, пролегающих в городе и в пригородных областях. Область применимости модели: – диапазон частот 800…2000МГц; – диапазон дальностей 20…5000м; – высота подвеса антенн базовой станции 4…50м; – высота подвеса антенны мобильного средства 1…3м. Исходные данные для расчета (рис.11.6): f – частота радиопередатчика, МГц; d – расстояние между передатчиком и приемником, км; hb – высота подвеса антенны базовой станции (БС), м; h 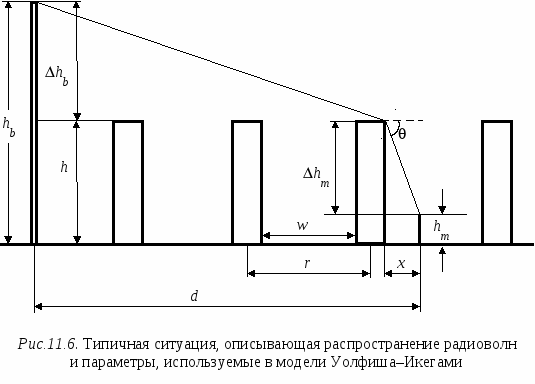 m – высота подвеса антенны мобильного средства (МС), м hb – высота приподнятости антенны БС над крышами домов (hb может быть положительным, отрицательным или равным нулю), м; hm – расстояние по высоте от крыши дома до антенны МС, м; Кроме того, в рассматриваемой области должны быть заданы: r – среднее расстояние между соседними улицами, м; w – средняя ширина улиц, м h – средняя высота зданий, м. Средняя высота зданий h может быть получена исходя из их этажности. Для типовых зданий высоту этажа берут равной 3м. Тогда h = 3м × число этажей + высота крыши (над последним этажом). Для острой крыши ее высоту полагают равной высоте этажа, т. е. 3м, для плоской – равной нулю. Теперь hb = hb– h hm = h– hm В модели рассматриваются два случая. 1. Распространение радиоволн происходит в пределах прямой видимости (вдоль улицы). В этом случае средние потери при распространении оцениваются выражением L = 42.6 + 26 lg d + 20 lg f (11.6) 2. Прямая видимость между передающей и приемной антенной отсутствует. Потери, определяющие уровень напряженности поля в месте расположения приемной антенны мобильного средства, определяются суммой вида: 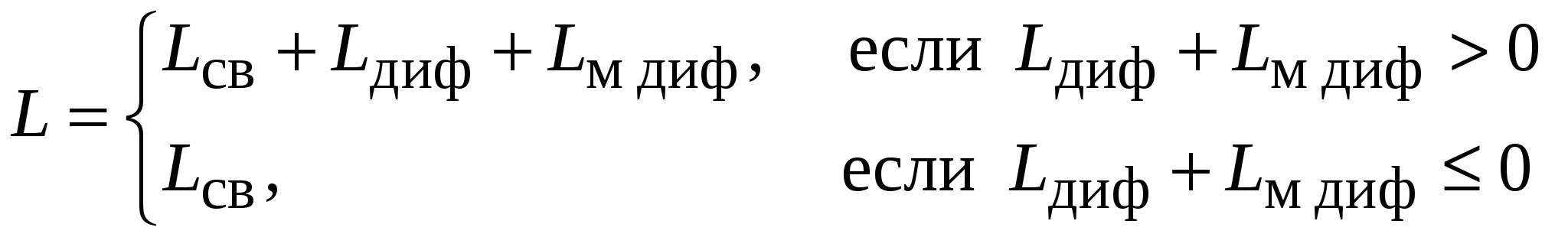 (11.7) (11.7)где Lсв – потери при распространении в свободном пространстве, дБ, (см.(11.4)); Lдиф – потери при рассеянии и дифракции электромагнитной волны на крыше здания, ближайшего к проезжей части улицы, где расположено мобильное средство, дБ; Lм диф – потери множественной дифракции и рассеяния, обусловленные рядами зданий, дБ. 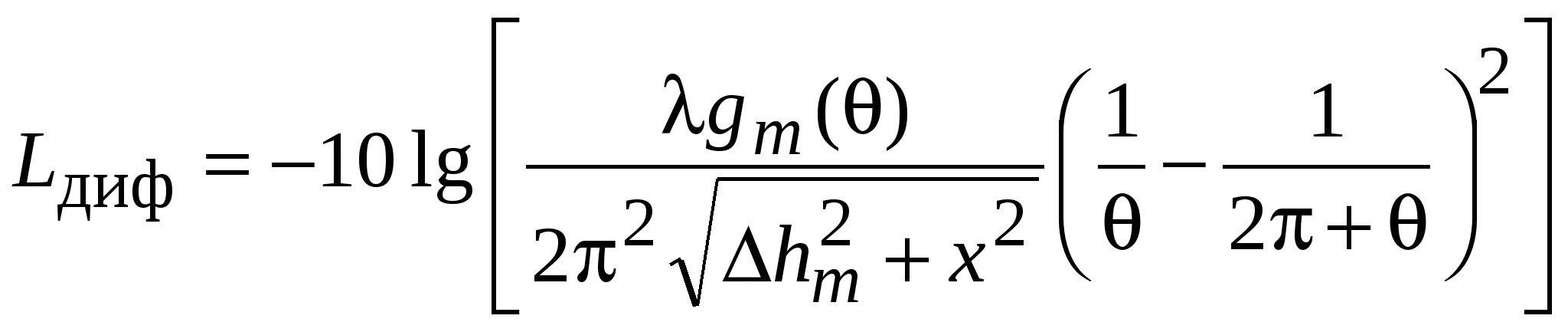 , (11.8) , (11.8)где gm(θ) – коэффициент усиления антенны мобильной станции в направлении на край крыши; = arctg(hm/x) – угол в радианах; – длина волны, м; x – расстояние между левой стеной улицы и антенной мобильного средства (0 xw), м. При расчетах чаще всего берут х = w/2. Lм диф= –10 lg(gbQ2), (11.9) г 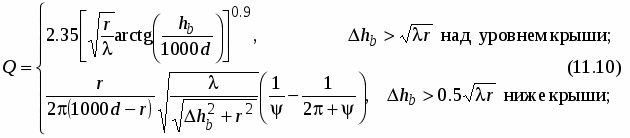 де gb – коэффициент усиления антенны базовой станции в направлении крыши (обычно принимается равным единице). и = arctg(–hb/r) Для промежуточных значений hb величину Q получают линейной интерполяции между значениями Q, соответствующими hb= Предполагая застройку территории, где находится мобильное средство, равновысотной, а застройку улиц двусторонней, для наиболее интересных частных случаев выражение (11.10) можно записать в несколько измененном виде: 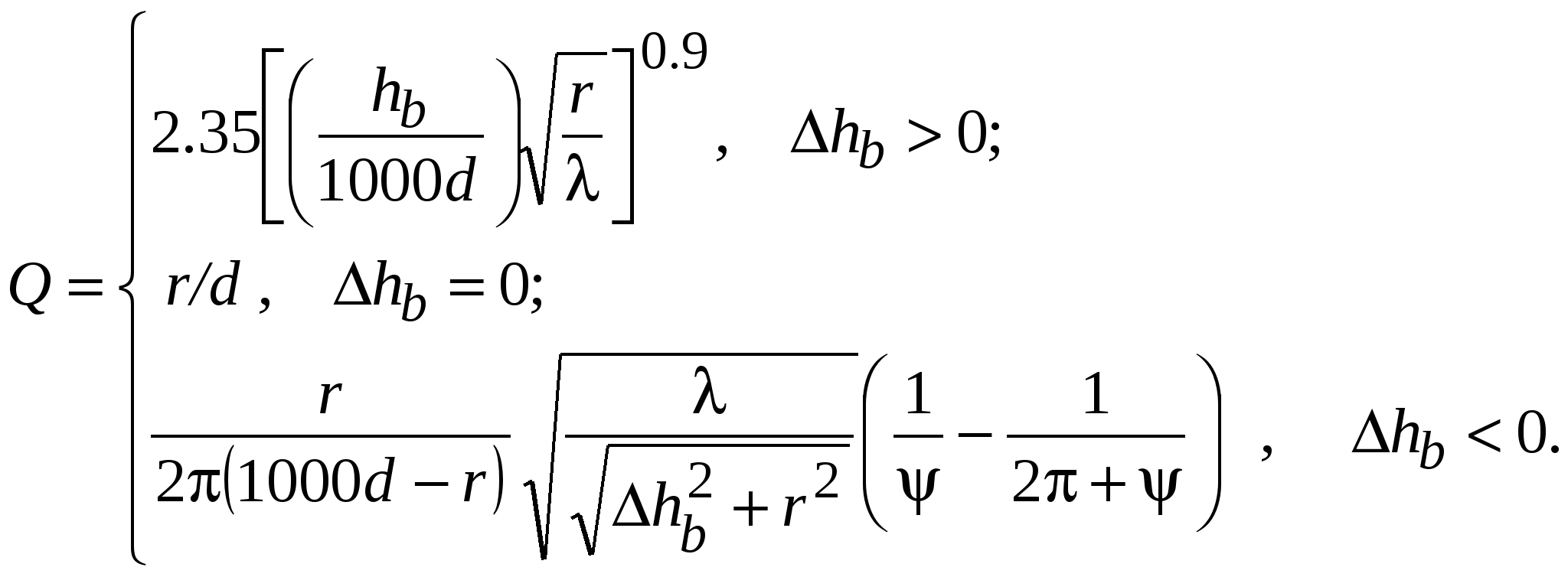 (11.11) (11.11)Модель COST231 Уолфиша-Икегами. Область применимости модели совпадает с областью применимости модели Уолфиша-Икегами, рассмотренной выше. Модель учитывает направление распространения радиоволны по отношению к направлению улицы, где находится приемная антенна, поэтому в исходные данные для расчета включен угол – угол между направлением улицы и направлением распространения радиоволны (рис.11.7). Остальные исходные данные такие же, как в модели Уолфиша-Икегами. 1. Для оценки потерь при распространении в пределах прямой видимости используют выражение (11.6). 2. Оценка потерь при распространении, когда прямая видимость между передающей и приемной антенной отсутствует, происходит согласно выражению (11.7), однако теперь Lдиф и Lм диф вычисляют по другим формулам: Lдиф = –16.9 – 10 lg w +10 lg f +20 lg hm +Lori , где 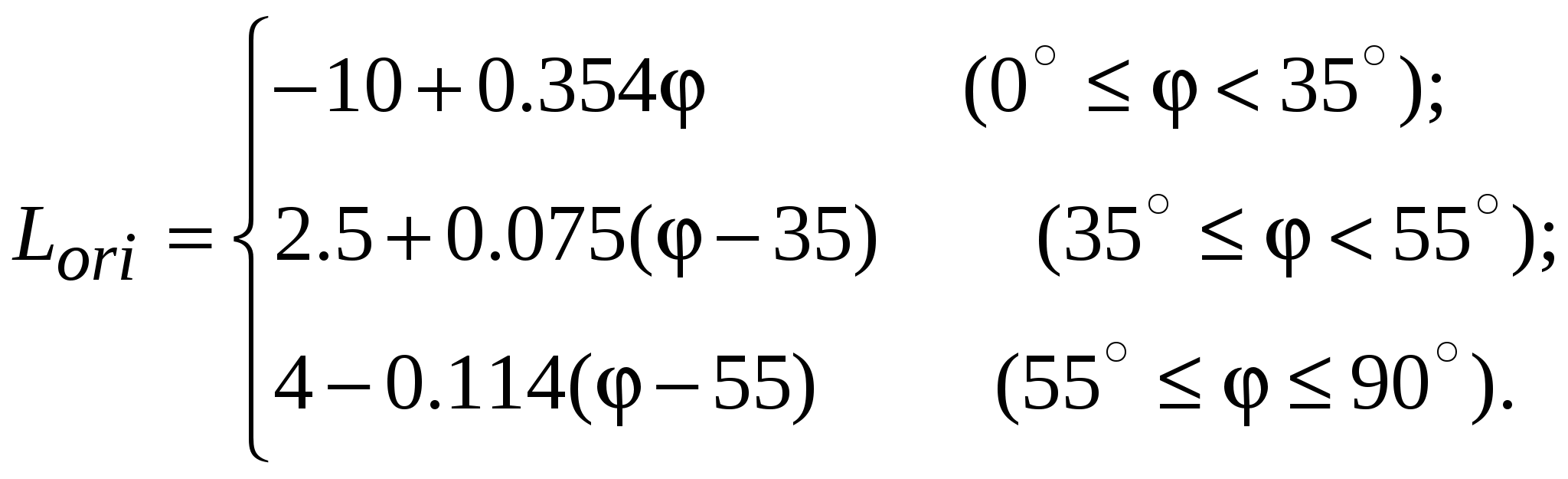 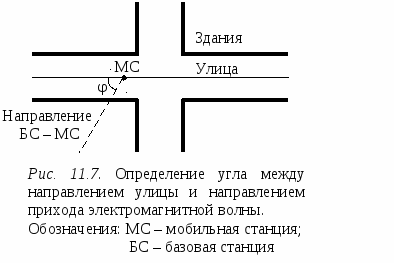 Lм диф = Lbsh+ ka+ kdlg d + kf lg f – 9 lg r, где 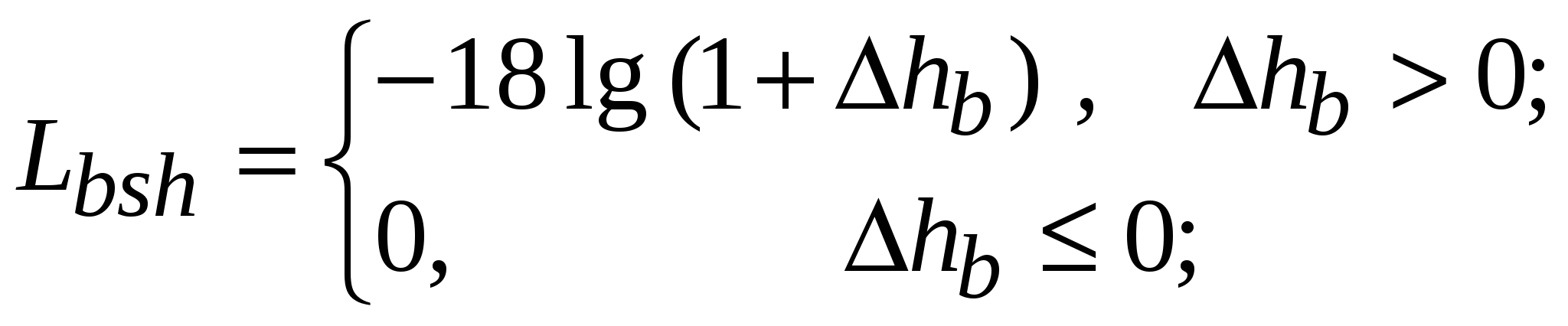 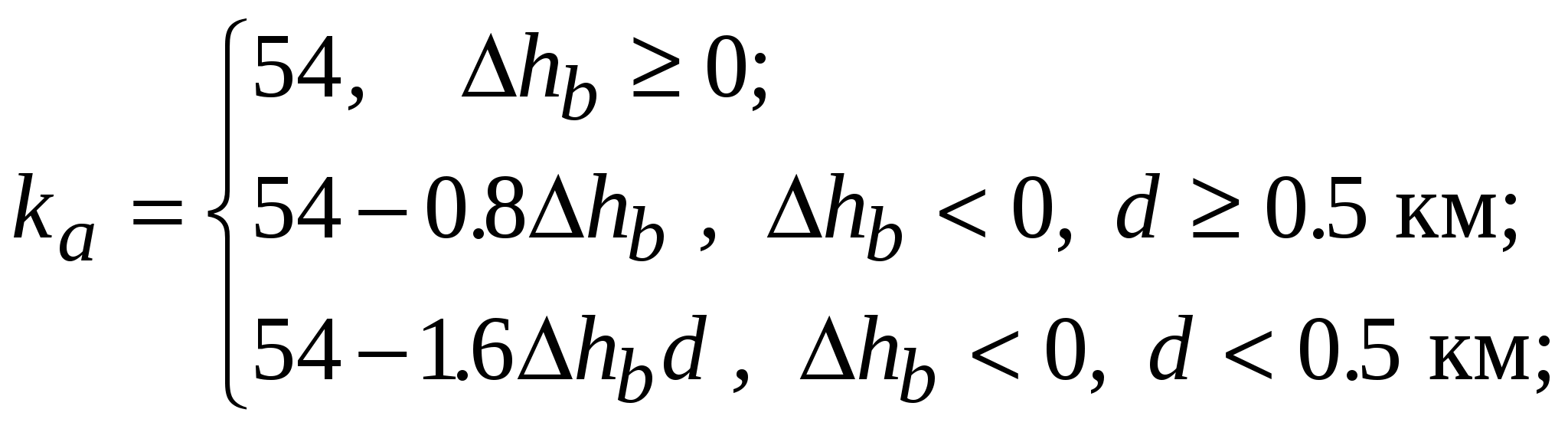 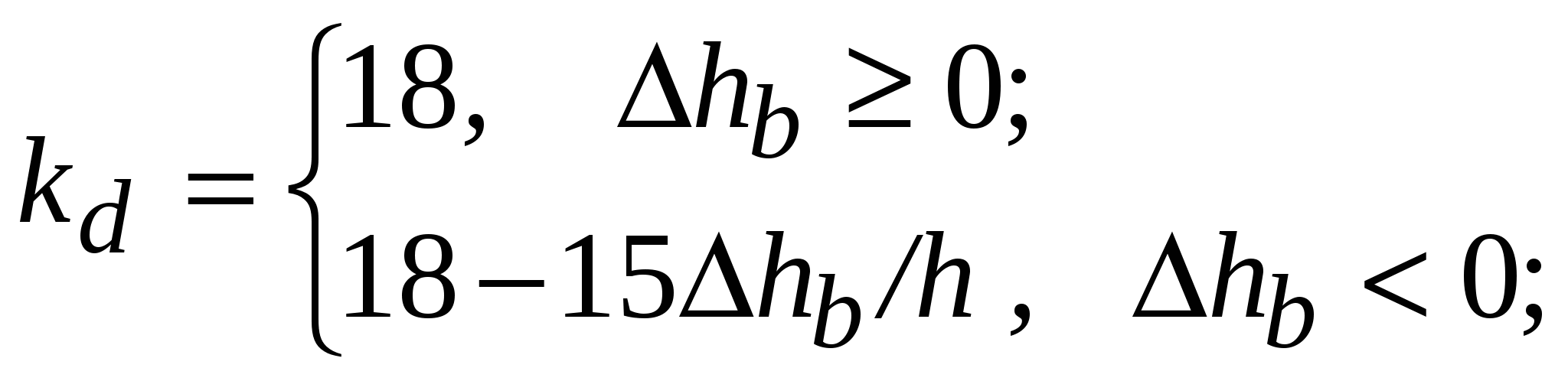 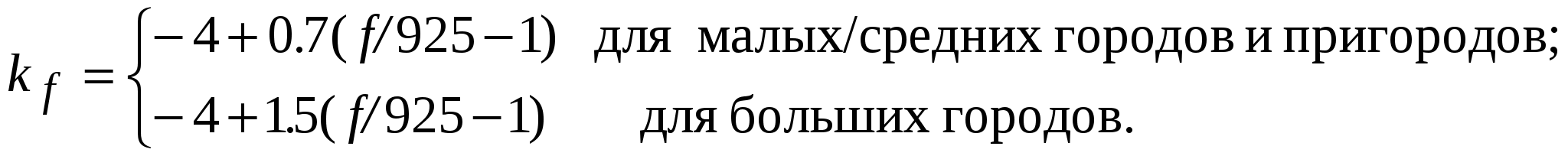
Как отмечалось раннее, явление дифракции состоит в огибании радиоволнами препятствий, встречающихся на пути их распространения. При этом потери сигнала на трассе распространения возрастают. Обычно потери на дифракцию оценивают отдельно в децибелах относительно свободного пространства, как это сделано, например, в рассмотренной выше модели Уолфиша-Икегами. В той модели речь шла, в частности, о множественной дифракции в условиях города. Однако, достаточно часто встречаются ситуации, когда на трассе распространения электромагнитной волны встречается незначительное число препятствий, которые могут вызвать явление дифракции. В этом случае обычно ограничиваются оценкой потерь на дифракцию, вызванных одним или двумя препятствиями. На трассе выделяют одно или два наиболее значительных препятствия и аппроксимируют их геометрическими телами (клином или цилиндром), для которых на основе общей теории дифракции получены математические выражения, позволяющие оценить потери на дифракцию на телах соответствующей формы. Теперь, используя эти выражения, выполняют оценку потерь на дифракцию. Модели, определяющие потери на дифракцию, в этом случае являются детерминистскими. При оценке полных потерь на трассе распространения потери на дифракцию суммируют с другими видами потерь, полученных по другим моделям и для других факторов, влияющих на распространение радиоволн. 11.5.1. Зоны Френеля.При распространении радиоволн над неровной поверхностью на величину потерь на трассе распространения влияют:
Для оценки влияния первых двух из перечисленных факторов используется такое понятие, как зоны Френеля. Чтобы пояснить это понятие, обратимся к рис.11.8, на котором представлена радиолиния, проходящая между точками А и В. В точке А находится антенна радиопередатчика, а точке В – антенна радиоприемного устройства. Используя точки A и B в качестве фокусов, вокруг этих точек можно построить эллипсоиды, называемые эллипсоидами Френеля. Эллипсоид Френеля – это пространство внутри эллипсоида, в фокусах которого находятся антенны, расположенные на концах радиолинии, а поверхность составляют точки, обладающие тем свойством, что разность длин трасс, проходящих через антенны и точки на поверхности эллипсоида, и трассы, соединяющей антенны напрямую, составляет n/, где n – целое положительное число. Для рис.11.8 это означает, что представленный на нем эллипсоид (а точнее его эллиптическое сечение) представляет эллипсоид Френеля, если разность длин трасс АСВ – АВ = nλ/2 Д 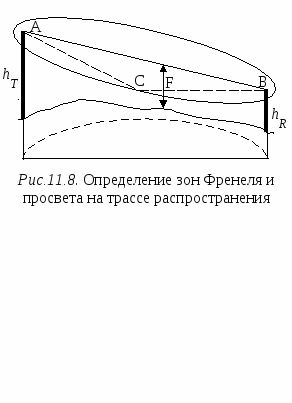 ля первого эллипсоида Френеля n = 1 и разность длин трасс составляет /, для второго эллипсоида Френеля n = 2 и, соответственно, разность длин трасс будет и т. д. ля первого эллипсоида Френеля n = 1 и разность длин трасс составляет /, для второго эллипсоида Френеля n = 2 и, соответственно, разность длин трасс будет и т. д.Зона Френеля порядка n – это область, расположенная между эллипсоидами n-го и (n– 1)-го порядков. Первая зона Френеля – это пространство внутри первого эллипсоида Френеля. Одной из важных характеристик трассы является просвет F (рис.11.8), который определяется из профиля трассы и представляет собой выраженный в метрах минимальный зазор между прямым лучом и поверхностью трассы. F 0, если поверхность трассы не перекрывает прямой луч, и F < 0 в противном случае. Радиотрасса имеет свободной первую зону Френеля, если в нее не попадают объекты, способные вызвать значительную дифракцию. Рассмотрим случай, когда просвет на трассе равен первой зоне Френеля, т. е. объект касается поверхности эллипсоида, огранивающего пространство этой зоны, но не заходит в нее, и оценим уровень сигнала в точке расположения приемной антенны. Обратимся к ситуации, когда отражениями от препятствия можно пренебречь. В терминах спирали Корню верхняя часть спирали участвует в формировании результирующего сигнала в приемной антенне полностью. В тоже время в нижней части спирали в формировании сигнала участвуют только те векторы, фаза которых не превышает 180, поскольку граница первой зоны Френеля соответствует разности хода лучей /2, т. е. 180. Таким образом, последний вектор, участвующий в формировании сигнала в нижней части спирали Корню, является первым вектором, который находится в противофазе с вектором прямой трассы и соответствует первому изгибу спирали Корню в нижней ее части после прохождения минимума (см. рис.11.2). Результирующий вектор сигнала в точке приема при этом близок к сигналу в свободном пространстве. Для количественной оценки потерь на дифракцию используют безразмерный параметр где d – разность длин трасс, одна из которых соединяет конечные точки радиолинии (т. е. точки расположения приемной и передающей антенн), а другая проходит от передающей антенны к приемной через вершину препятствия. По соглашению, – положительное, если прямая трасса блокирована препятствием (препятствие имеет «положительную высоту») и – отрицательное, если трасса имеет просвет («отрицательная высота»). Если прямая трасса касается вершины препятствия, = 0. Когда просвет равен первой зоне Френеля, d = /2 и из (11.12) = –1.4. На спирали Корню эта точка соответствует первому повороту вектора на 180. Уровень сигнала при этом будет даже несколько выше, чем в свободном пространстве. Точка = –1 соответствует d = /4 и последний вектор, участвующий в суммировании на спирали Корню, повернут на 90 по отношению к вектору прямой трассы и находится на самой нижней точке спирали. В этом случае также имеет место небольшое усиление (около 1.2 дБ) по сравнению со свободным пространством. Отметим, что можно оставить до 60% просвета в первой зоне Френеля ( = – 0.85) без существенных потерь по отношению к свободному пространству. Это видно также из графиков, изображенных на рис.11.9. На рис.11.9 представлена зависимость потерь на дифракцию относительно свободного пространства от размера просвета на трассе относительно первой зоны Френеля [52]. Параметром изображенных кривых является безразмерный индекс кривизны для вершины препятствия. Как видно из этих кривых, минимальные потери на дифракцию имеют место для препятствий в виде клина, максимальные – для гладкой сферы. Препятствия, имеющие промежуточный индекс кривизны, вносят потери на дифракцию, лежащие между этими значениями. Однако, вне зависимости от вида препятствия, если отношение просвета F к радиусу первой зоны Френеля F1 имеет значение 0.6, дополнительные потери на дифракцию отсутствуют. Для того чтобы просвет составлял первую зону Френеля, расстояние от ближайшей точки препятствия до прямой трассы должно быть, по крайней мере где d1 и d2 расстояния от вершины препятствия до двух конечных точек радиолинии. Э 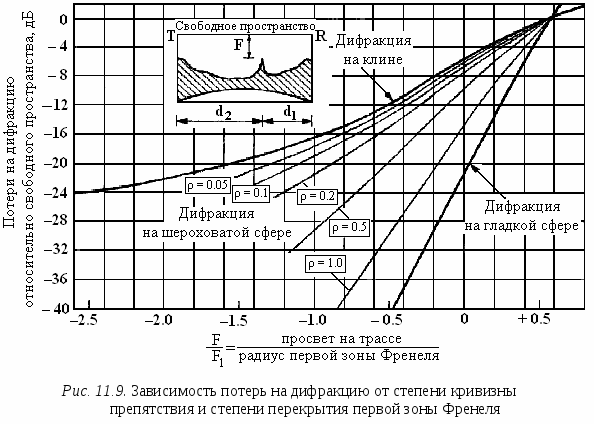 та формула является аппроксимацией и не справедлива в областях очень близких к конечным точкам радиотрассы. Если = 0 (нулевой просвет) и вершина препятствия очень узкая (нет существенных отражений, например, узкое клиновидное препятствие), потери на дифракцию, как было показано в разделе 11.1 (см. также рис.11.9), составляют 6 дБ. Однако такая модель препятствия может не всегда соответствовать реальной ситуации. Вершина препятствия может быть скругленной или иметь большую плоскую поверхность (как, например, крыши зданий). В этих случаях при нулевом просвете потери могут быть значительно выше, и во многих случаях более достоверной оценкой служит значение 20 дБ. Поэтому на реальных трассах очень важно иметь свободной первую зону Френеля и уметь производить оценку потерь на дифракцию, если объекты на трассе перекрывают ее. Нужно иметь в виду, что зона Френеля трехмерная, и просвет должен быть обеспечен со всех сторон от прямой трассы. Остановимся на некоторых подходах, используемых для оценки потерь на дифракцию. 11.5.2. Дифракция на клинеП 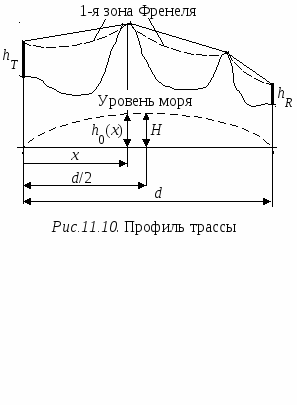 ервоначально в прямоугольной системе координат с помощью картографической базы данных строят топографический профиль трассы, используя информацию о высотах соответствующих точек местности над дугой земной поверхности (уровнем моря) (рис. 11.10). Уравнение для дуги земной поверхности соответствует уравнению параболы, которая между точками расположения передатчика и приемника имеет форму близкую к окружности и при нормальной рефракции атмосферы записывается в виде: ервоначально в прямоугольной системе координат с помощью картографической базы данных строят топографический профиль трассы, используя информацию о высотах соответствующих точек местности над дугой земной поверхности (уровнем моря) (рис. 11.10). Уравнение для дуги земной поверхности соответствует уравнению параболы, которая между точками расположения передатчика и приемника имеет форму близкую к окружности и при нормальной рефракции атмосферы записывается в виде:h0(x) = x(d x)/17, где x и d выражены в километрах, а h0 – в метрах Высота дуги, соответствующая x= d/2 (максимальная высота дуги) H = d2/68 Здесь Hвыражена в метрах, а d в километрах. Д 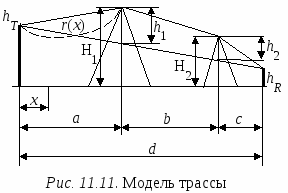 алее препятствия заменяют телами в форме клина. Обычно выдвигается требование, что максимальная ширина препятствия не превышает d/20. Реальная трасса заменяется моделью (рис.11.11). При построении модели учитывают значение h0(x), а также требование, чтобы в модели при оценке дифракционных потерь на трассе между передатчиком (или приемником) и клиновидным препятствием (или между клиновидными препятствиями) первая зона Френеля не перерывалась. Радиус первой зоны Френеля r(x) (рис.11.11) рассчитывают используя выражение: для 0 x a где r(x) – рассчитывается в метрах; x и a – расстояния, км; f – частота, МГц;. Аналогичные выражения могут быть записаны для других участков трассы с заменой «а» на «b» или «с» соответственно. В зависимости от числа клиновидных препятствий на трассе расчеты выполняют следующим образом. Одно препятствие. Этот случай изображен на рис.11.12 а и б, где представлены возможные положения препятствия на трассе между передатчиком и приемником. Расчет выполняют в следующем порядке. 1. Определяют степень перекрытия трассы препятствием (приведенную высоту препятствия): 2 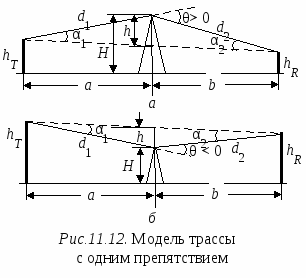 . Используя геометрические параметры, описывающие взаимное положение передатчика, приемника и препятствия на трассе, смысл которых ясен из рис.11.12, вычисляют безразмерный параметр по одной из следующих формул [53]: . Используя геометрические параметры, описывающие взаимное положение передатчика, приемника и препятствия на трассе, смысл которых ясен из рис.11.12, вычисляют безразмерный параметр по одной из следующих формул [53]: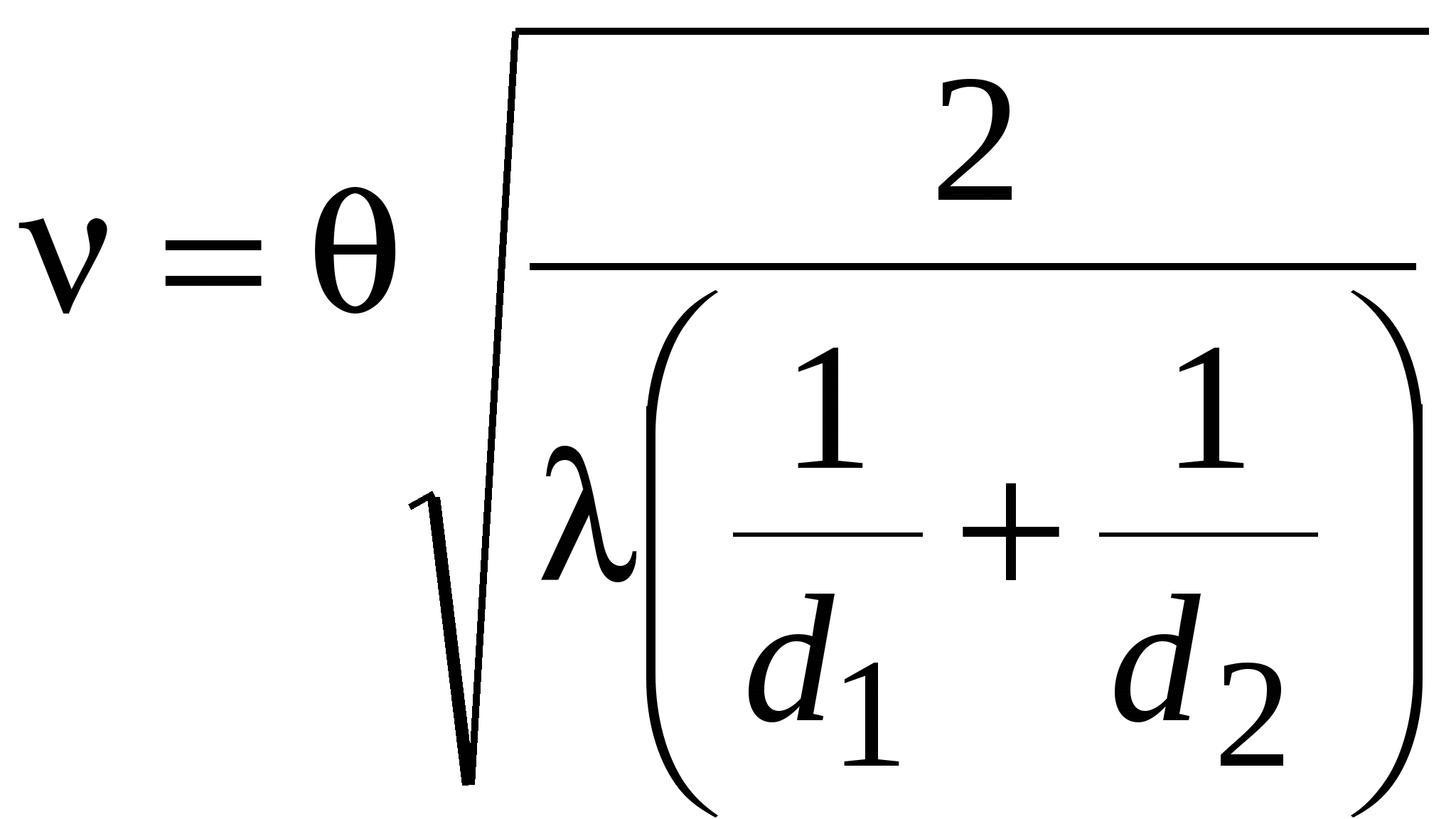 (11.15б) (11.15б)3. Если полученное значение > 0.7, то приближенное значение потерь на дифракцию оценивают, используя выражение: Если < 0.7, полагают Lдиф() = 0 дБ. Д 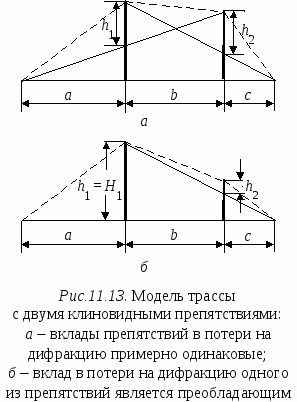 ва препятствия. Модели трассы с двумя клиновидными препятствиями представлены на рис. 11.13, а и б [53]. При оценке потерь на трассе с двумя препятствиями одно из препятствий может быть главным или доминантным, т. е. вносить вклад в потери на дифракцию значительно больше, чем второе. Для определения, является ли какое либо из препятствий главным, следует вычислить приведенные высоты клиновидных препятствий h1 и h2 (рис.11.13, а): ва препятствия. Модели трассы с двумя клиновидными препятствиями представлены на рис. 11.13, а и б [53]. При оценке потерь на трассе с двумя препятствиями одно из препятствий может быть главным или доминантным, т. е. вносить вклад в потери на дифракцию значительно больше, чем второе. Для определения, является ли какое либо из препятствий главным, следует вычислить приведенные высоты клиновидных препятствий h1 и h2 (рис.11.13, а):И далее определить главное препятствие, исходя из выполнения неравенств: – если – если Если левая и правая части неравенств отличаются незначительно, доминантное препятствие отсутствует. В связи с этим можно выделить две возможные ситуации. 1. Вклады в общие потери на дифракцию, вносимые каждым препятствием, различаются незначительно (примерно одинаковые) (рис.11.13, а). В этом случае, используя методику оценки потерь для одиночного препятствия, рассмотренную выше, рассчитывают потери, вносимые каждым препятствием по отдельности. При этом вершина первого препятствия рассматривается как источник сигнала, который испытывает дифракцию на втором препятствии. Первая трасса, для которой вычисляется параметр по одной из формул (11.15а)– (11.15г) и Lдиф1() по (11.16), определяется расстояниями a и b и высотой h1. Источник сигнала – начало трассы, приемник – вершина второго препятствия. Вторая трасса, для которой по тем же формулам вычисляют и Lдиф2(), определяется расстояниями b и c и высотой h2. Источник сигнала – вершина первого препятствия, приемник – конечная точка трассы. Если каждый из вкладов Lдиф1 и Lдиф2 превышает примерно 15 дБ, то чтобы учесть разнос по расстоянию между клиновидными препятствиями, нужно оценить корректирующий член Lc, используя формулу: Полные потери на дифракцию определяются суммой: Lдиф = Lдиф1 + Lдиф2 + Lc 2. Одно из препятствий является доминантным (главным) (первое на рис 11.13, б). В этом случае оценивают только потери на дифракцию, вносимые каждым препятствием по отдельности. Однако трасса для преобладающего препятствия определяется расстояниями a и (b + c) и приведенной высотой h1, которая совпадает с реальной высотой главного препятствия (рис.11.13, б). Трасса для оценки дифракции на втором препятствии определяется расстояниями b и c и приведенной высотой h2, которую рассчитывают, используя (11.14). Потери, соответствующие этим трассам, суммируют. Эту сумму принимают за полные потери на дифракцию на трассе. Корректирующий член (11.16) не рассчитывают и не производят никакой дополнительной коррекции полученного результата. 11.5.3. Дифракция на цилиндреВ большинстве ситуаций препятствия, встречающиеся на местности, не похожи на простой клин и аппроксимация их клином недооценивает потери на дифракцию. Существуют различные способы решения этой задачи. Один из них состоит в том, что вершину препятствия моделируют цилиндром радиуса r , как показано на рис.11.14. Чтобы рассчитать потери, необходимо нарисовать профиль объекта и провести прямые линии из конечных точек линии связи так, чтобы они касались самых высоких частей объекта, которые видны из индивидуальных ракурсов. Далее оценивают параметры Ds, d1, d2 и вычисляют 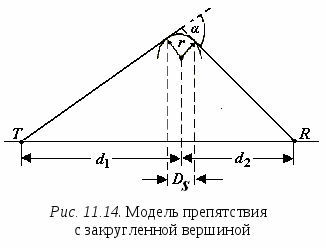 , ,где измеряется в радианах. Далее вычисляют потери на дифракцию на клине, образованном касательными к препятствию, и дополнительные потери При вычислении дополнительных потерь применяется коррекция этих потерь на неровность: если объект, например, холм, вершина которого покрыта деревьями, а не гладкая, то дополнительные потери составят примерно только 65% от потерь, вычисленных согласно (11.17). В общем случае более гладкие объекты дают более высокие потери на дифракцию. Аналогичный способ оценки потерь на дифракцию на препятствии с закругленной вершиной, но со своим методом определения дополнительных потерь представлен в [53]. Еще один вариант оценки потерь на препятствии со скругленной вершиной описан в [52]. Анализируя кривые, приведенные на рис. 11.9, можно установить, что дополнительные потери на дифракцию на препятствиях с фиксированным безразмерным показателем кривизны по отношению к потерям на клине пропорциональны разности потерь на дифракцию на гладкой сфере и клине. Для каждого значения коэффициент пропорциональности есть величина постоянная и не зависит от отношения F/F1. Обозначим его R. Коэффициент пропорциональности R в [52] назван коэффициентом эквивалентной закругленности. Дифракция на клине соответствует R = 0, а на гладкой сфере R= 1 (земля без препятствий). Для препятствий, имеющих 0 < R < 1, потери на дифракцию Lдиф вычисляют, используя выражение Lдиф = Lкл + R( Lсф – Lкл ) (11.18) Пусть x= F/F1. Тогда граничные кривые, определяющие на рис. 11.9 потери на клине и на гладкой сфере, можно аппроксимировать выражениями Lсф= –38.68x + 21.66 (11.19) 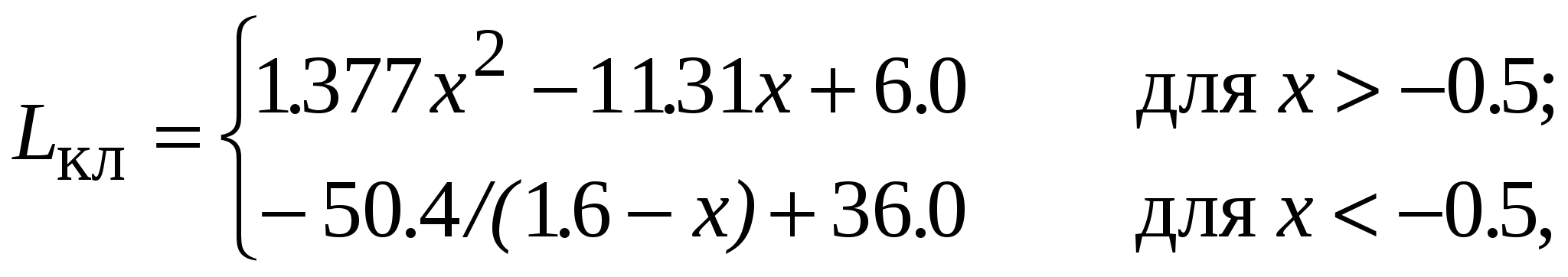 (11.20) (11.20)где Lсф и Lкл соответственно потери на дифракцию на гладкой сфере и на клине по отношению к свободному пространству, дБ, а x 0.6. Просвет F определяют исходя из географических данных о возвышениях на трассе распространения и ходе прямого луча, связывающего передающую и приемную антенны. В качестве главного препятствия рассматривают препятствие, для которого просвет на трассе минимален. Радиус первой зоны Френеля в месте расположения препятствия в метрах дает выражение где c – скорость света, км/с; d1, d2 – расстояния от передатчика и приемника до главного препятствия, км; d = d1 + d2 – длина трассы, км; f – частота, МГц. На основе статистического анализа данных о корреляционных связях между отсчетами уровней местности для вычисления R предложена следующая формула R = 75/(H + 75), где H определяется следующим образом: в окрестности главного препятствия, равной 10 км, вдоль трассы берут отсчеты уровней местности. Для полученных отсчетов по методу наименьших квадратов строят прямую. Далее вычисляют среднеквадратическое отклонение отсчетов относительно построенной прямой. В качестве H берут значение, равное 90% от среднеквадратического отклонения. |