ИДЗ_Физика. Ее задание 1
 Скачать 50.64 Kb. Скачать 50.64 Kb.
|
|
ее задание №1. Вариант № 3. 1. Радиус-вектор материальной точки изменяется со временем по закону: 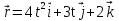 . Определите: а) скорость . Определите: а) скорость  ; б) ускорение ; б) ускорение 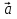 в момент времени t = 2 с. в момент времени t = 2 с.2. Работа, затраченная на толкание ядра, брошенного под углом = 15 к горизонту, равна 800 Дж. Масса ядра 8 кг. На каком расстоянии от места бросания ядро упадет на Землю? Принять g = 10 м/с.2 . Результат представьте в единицах СИ. 3. Частица 1 массой m1, летящая со скоростью , столкнувшись с неподвижной частицей 2 массой М, отскакивает от нее и летит в противоположном направлении со скоростью u1 = /2. Найдите: а) скорость частицы 2 после столкновения; б) энергию, которая пошла на нагревание и деформацию. 4. Маховик радиусом R = 10 см может без трения вращаться вокруг горизонтальной оси. На обод маховика намотан шнур, к которому привязан груз массой m = 800 г. Опускаясь равноускорено, груз прошел расстояние l = 160 см за время t = 2 c. Определите момент инерции I маховика. 5. Какую скорость нужно сообщить ракете, чтобы она не вернулась на Землю? Сопротивление атмосферы можно не учитывать. g = 9,8 м/с2; R3 = 6370 км. 6. Найдите импульс, полную и кинетическую энергии электрона, движущегося со скоростью = 0,9 с, где с = 3108м/с. Масса покоя электрона m0 = 9,110-31 кг. 7. В некоторой среде распространяется волна. За время, в течение которого частица среды совершает 150 колебаний, волна распространяется на 110 м. Найдите длину волны. Результат представьте в единицах СИ и округлите до десятых. 8. Напишите уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с2 , период колебаний 2 с, смещение точки от положения равновесия в начальный момент времени равно 25 мм. Задача №1. Радиус-вектор материальной точки изменяется со временем по закону: 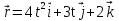 . Определите: а) скорость . Определите: а) скорость 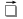 ; б) ускорение ; б) ускорение 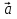 в момент времени t = 2 с. в момент времени t = 2 с.Дано: 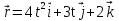 ; t = 2 с. ; t = 2 с.Найти: 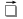 = ?; = ?; 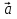 = ?; = ?; 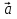 1 = ?. 1 = ?.Решение: Скорость 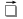 , равна первой производной по времени t от координат радиус-вектора , равна первой производной по времени t от координат радиус-вектора 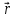 движущейся материальной точки: движущейся материальной точки: 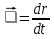 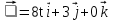 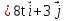 Ускорение 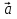 , равно первой производной от скорости υ: , равно первой производной от скорости υ: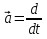 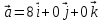 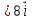 Ускорение 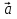 1 в момент времени t = 2: ускорение это первая производная от скорости и от времени не зависит: 1 в момент времени t = 2: ускорение это первая производная от скорости и от времени не зависит: 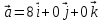 , то , то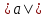 = = 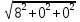 = = 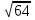 = 8 м/с2. = 8 м/с2.Ответ: 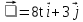 ; ; 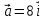 ; ; 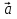 1 = 8 м/с2. 1 = 8 м/с2.Задача №2. Работа, затраченная на толкание ядра, брошенного под углом = 15 к горизонту, равна 800 Дж. Масса ядра 8 кг. На каком расстоянии от места бросания ядро упадет на Землю? Принять g = 10 м/с2. Результат представьте в единицах СИ. Дано: = 15; А = 800 Дж; 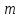 = 8 кг; g = 10 м/с2. = 8 кг; g = 10 м/с2.Найти: L = ? Решение: Работа затраченная на толкание ядра равна изменению его кинетической энергии: A = ΔEk , 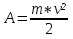 => => 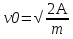 . .Траектория движения ядра, брошенного под углом к горизонту, парабола. Следовательно, ядро движется в двух направлениях, по вертикали и по горизонтали. Движение по горизонтали равномерное с постоянной скоростью v0(x). Определим расстояние, которое преодолело ядро по оси ОХ, напишем уравнение координаты для оси ОХ: L = v0(x)*t = v0*cosα*t. Нам неизвестно время полета, но мы знаем, что время подъема до верхней точки параболы равно времени падения с нее. Найдем время подъема до максимальной высоты: v(y) = v0(y) - g*t, 0 = v0*sinα - g*t, 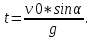 Полное время полета равно: 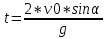 , подставим значение v0, получим t равное: , подставим значение v0, получим t равное: 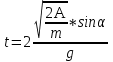 , , В формулу для L подставляем значения t и v0: L = v0*cosα*t = 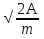 * cosα* * cosα*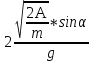 = = 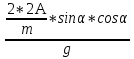 = = 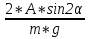 В полученную формулу для L подставляем численные значения: L = 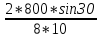 = 10 метров. = 10 метров.Ответ: L = 10 метров. Задача №3. Частица 1 массой m1, летящая со скоростью , столкнувшись с неподвижной частицей 2 массой М, отскакивает от нее и летит в противоположном направлении со скоростью u1 = /2. Найдите: а) скорость частицы 2 после столкновения; б) энергию, которая пошла на нагревание и деформацию. Дано: m1; ; М; u1 = /2; Найти: V = ?; Е = ? Решение: Согласно закону сохранения импульса: p1 = p2, m1* + М*0 = - m1*u1 + M*V m1* = - m1*u1 + M*V m1* + m1*u1 = M*V; подставим значение u1 = /2, m1* + m1*/2 = M*V 1,5*m1 = M*V 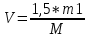 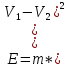 , где , где 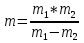 , V1 - скорость первой частицы; V2 - скорость второй частицы. , V1 - скорость первой частицы; V2 - скорость второй частицы.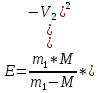 Ответ: 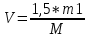 ; ; 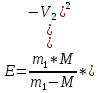 Задача №4. Маховик радиусом R = 10 см может без трения вращаться вокруг горизонтальной оси. На обод маховика намотан шнур, к которому привязан груз массой m = 800 г. Опускаясь равноускорено, груз прошел расстояние l = 160 см за время t = 2 c. Определите момент инерции I маховика. Дано: R = 10 см = 0,1 м; m = 800 г = 0,8 кг; l = 160 см = 1,6 м; t = 2 c. Найти: I = ? Решение: По основному уравнению динамики вращательного движения M = I*ɛ => I = 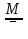 По третьему закону Ньютона: m*g - T = m*a => T = m*(g - a), момент определяется по формуле : M = T*R, подставляем в нее значение Т: M = T*R => M = m*(g - a)*R. При равноускоренном движении: l 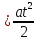 => a => a 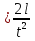 , => , =>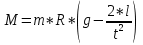 Угловое и линейное ускорение связаны соотношением: 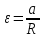 , и подставляем сюда значение линейного ускорения: , и подставляем сюда значение линейного ускорения: 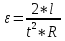 Подставим полученные выражения для ɛ и M в первую формулу, получим: 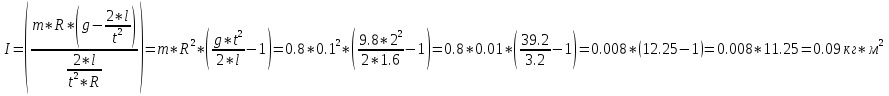 Ответ: I = 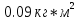 Задача №5. Какую скорость нужно сообщить ракете, чтобы она не вернулась на Землю? Сопротивление атмосферы можно не учитывать, g = 9,8 м/с2; R3 = 6370 км. Дано: g = 9,8 м/с2; R3 = 6370 км. Найти: V0 = ? Решение: При удалении ракеты от Земли будет увеличиваться ее потенциальная энергия 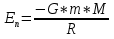 и уменьшаться кинетическая и уменьшаться кинетическая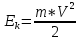 . По закону сохранения энергии: уменьшение кинетической энергии равно увеличению потенциальной: Ek0 – Ek = EП – EП0 . По закону сохранения энергии: уменьшение кинетической энергии равно увеличению потенциальной: Ek0 – Ek = EП – EП0 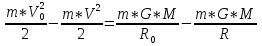 , ,где m - масса ракеты; M - масса Земли; G - гравитационная постоянная; V0 - скорость ракеты относительно Земли в начальный момент; V - скорость ракеты относительно Земли в рассматриваемый моменты; R0 - расстояние от центра Земли до ракеты в начальный момент; R - расстояние от центра Земли до ракеты в рассматриваемый момент; 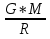 – потенциал поля тяготения Земли на расстоянии R от центра Земли. – потенциал поля тяготения Земли на расстоянии R от центра Земли.Сокращая обе части равенства на m и преобразуя ее получим: 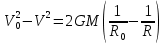 Ракета не вернется на Земля если ее скорость V = 0 при R = , тогда 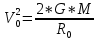 Из закона всемирного тяготения следует, что на поверхности Земли 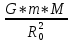 = m*g G*M = g* = m*g G*M = g*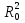 , где g = 9,8 м/с2 – ускорение свободного падения на поверхности Земли. , где g = 9,8 м/с2 – ускорение свободного падения на поверхности Земли.Подставляя значение G*M в первое равенство мы найдем V0: 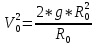 V0 = V0 = 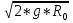 = = 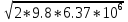 = = 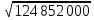 = == 11 174 м/с = 11,174 км/с. Ответ: V0 = 11,174 км/с. Задача №6. Найдите импульс, полную и кинетическую энергии электрона, движущегося со скоростью = 0,9 с, где с = 3108м/с. Масса покоя электрона m0 = 9,110-31 кг. Дано: = 0,9*с; с = 3108м/с; m0 = 9,110-31 кг. Найти: p, E, Ek = ? Решение: Импульс находим по формуле: p = m0*c = 9,110-31*0,9*3108 = 24,57*10-23 кг*м/с. Кинетическая энергия:   Полная энергия:   9,110-31*9*1016 + 9,110-31*9*1016 + 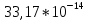 = = = 4,136*10-13 Дж. Ответ: p = 24,57*10-23 кг*м/с; 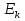 = = 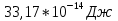 ; ; 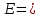 4,136*10-13 Дж. 4,136*10-13 Дж.Задача №7. В некоторой среде распространяется волна. За время, в течение которого частица среды совершает 150 колебаний, волна распространяется на 110 м. Найдите длину волны. Результат представьте в единицах СИ и округлите до десятых. Дано: n = 150; l = 110 м. Найти: λ = ? Решение: Длина волны это расстояние пройденное волной за время равное одному периоду колебания частиц волны, связана со скоростью ее распространения соотношением: λ = v*T. Из условия задачи следует, что: v =  Период колебаний, как время одного колебания, может быть выражен по формуле: T =  Подставляем значения для v и T в первую формулу, длинны волны, и получаем: λ =  => λ = => λ =  ≈ 0.73 м. ≈ 0.73 м.Ответ: λ ≈ 0.73 м. Задача №8. Напишите уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с2 , период колебаний 2 с, смещение точки от положения равновесия в начальный момент времени равно 25 мм. Дано: amax = 49,3 см/с2 = 0,493 м/с2; T = 2 c; x0 = 25 мм = 0,025 м. Найти: x(t) = ? Решение: Уравнение гармонических колебаний выглядит следующим образом: x = A*sin(ω0*t + φ0), где А - амплитуда; ω0 - циклическая частота колебание; (ω0*t + φ0) - фаза колебаний; φ0 - начальная фаза. Из формулы модуля максимального ускорения: = A* 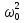 , выразим амплитуду: A = , выразим амплитуду: A = 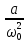 , так как ω0 = , так как ω0 = 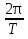 , тогда амплитуда будет равна: , тогда амплитуда будет равна:A = 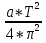 = = 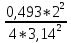 = 0,05 м. = 0,05 м.Начальную фазу φ0 найдем зная x0, из условия что t = 0, a x = x0, тогда наше уравнение колебания примет вид: x0 = A*sin φ0, откуда φ0 = arcsin 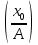 = arcsin = arcsin 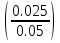 = arcsin (0.5) = 30O. = arcsin (0.5) = 30O.Подставим полученные значения A, ω0 и φ0 в уравнение гармонического колебания и получим: x(t) = 0,05*sin ( 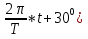 = = 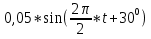 = 0,05*sin (π*t + 30O) = 0,05*sin (π*t + 30O)Ответ: x(t) = 0,05*sin (π*t + 30O), м. |
