Егэ. Даша ЕГЭ 2015 Математика. Егэ 2015 Математика Задание 21
 Скачать 13.93 Kb. Скачать 13.93 Kb.
|
|
ЕГЭ 2015 Математика Задание 21. Каждый из группы учащихся сходил в кино или театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более  от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более  от общего числа учащихся группы, посетивших кино. от общего числа учащихся группы, посетивших кино. а) Могло ли быть в группе 8 мальчиков, если дополнительно известно, что всего в группе было 16 учащихся? б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 16 учащихся? в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б? Решение. а) Если группа состоит из 3 мальчиков, посетивших только театр, 5 мальчиков, посетивших только кино, и 8 девочек, сходивших и в театр, и в кино, то условие задачи выполнено. Значит, в группе из 16 учащихся могло быть 8 мальчиков. б) Предположим, что мальчиков было 9 или больше. Тогда девочек было 7 или меньше. Театр посетило не более 3 мальчиков, поскольку если бы их было 4 или больше, то доля мальчиков в театре была бы не меньше  , что больше , что больше  . Аналогично кино посетило не более 5 мальчиков, поскольку . Аналогично кино посетило не более 5 мальчиков, поскольку 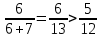 , но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию. , но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.В предыдущем пункте было показано, что в группе из 16 учащихся могло быть 8 мальчиков. Значит, наибольшее количество мальчиков в группе – 8. в) Предположим, что некоторый мальчик сходил и в театр, и в кино. Если бы вместо него в группе присутствовало два мальчика, один из которых посетил только театр, а другой – только кино, то доля мальчиков и в театре, и в кино осталась бы прежней, а общая доля девочек стала бы меньшей. Значит, для оценки наименьшей доли девочек в группе можно считать, что каждый мальчик сходил или только в театр, или только в кино. Пусть в группе  мальчиков, посетивших театр, мальчиков, посетивших театр, 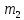 мальчиков, посетивших кино, и мальчиков, посетивших кино, и  девочек. Оценим долю девочек в этой группе. Будем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится. девочек. Оценим долю девочек в этой группе. Будем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.По условию 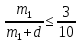 , ,  , значит, , значит,  , ,  . Тогда . Тогда  , поэтому доля девочек в группе: , поэтому доля девочек в группе: 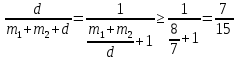 . . Если группа состоит из 3 мальчиков, посетивших только театр, 5 мальчиков, посетивших только кино, и 7 девочек, сходивших и в театр, и в кино, то условие задачи выполнено, а доля девочек в группе равна  . .Ответ: а) да; б) 8; в)  . . |
