Эконометрические модели формирования финансовых активов кредитных организаций ПФО. Курсовая. Эконометрические модели формирования финансовых активов кредитных организаций пфо
 Скачать 436.93 Kb. Скачать 436.93 Kb.
|
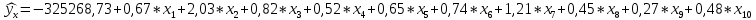 Для построения модели множественной регрессии проверили факторные признаки на отсутствие интеркоррелированности. Была построена матрица парных коэффициентов корреляции (таблица 1). Таблица 1 – Матрица парных коэффициентов корреляции
Определитель данной матрицы составил 0,000001044. Это свидетельствует о присутствии сильной мультиколлинеарности факторных признаков. Наличие мультиколлинеарности также проверялось с помощью 𝜒2– критерия. Значение 𝜒2набл составило 475,14, в то время как 𝜒2табл = 73,31. Наличие мультиколлинеарности подтверждено, так как 𝜒2набл>𝜒2табл. Далее были исключены мультиколлинеарные факторы, то есть факторы, которые в большей степени связаны между собой. Факторы были исключены с помощью пошагового метода с включением в программе «Statistika». Ниже представлена таблица итоговых статистик множественной модели регрессии. Таблица 2 – Итоговые статистики модели регрессии
Условие достаточности количества наблюдений было выполнено, так как уравнение множественной регрессии было построено по 40 наблюдениям, данное число превышало число объясняющих переменных. Модель более качественна, если коэффициент детерминации приближен к единице. Видим, что у данной модели коэффициент детерминации равен 0,996. Значение данного индекса стремится к 1. Таким образом, вариация переменной y – активы банков ПФО на 99,6% объясняется вариацией четырех факторов. Остальные 0,4% приходятся на другие факторы, не учтенные в модели. Коэффициент корреляции составил 0,992. Связь прямая, сильная, так как находится в соответствующем диапазоне от 0,7 до 1. Точность модели доказывалась с помощью расчета стандартной ошибки оценки. Ошибка была равна 2314417, она меньше, чем значение 16248816 – 10% от среднего значения результативного признака, поэтому модель признается точной. Рассчитанное наблюдаемое значение F-критерия Фишера при степенях свободы 4 и 35 составило 1108,285, оно больше его табличного значения 5,6, поэтому уравнение в целом считается статистически значимым и надежным с уровнем значимости 95%. Далее была построена таблица с итогами регрессии для зависимой переменной регрессионной модели. Таблица 3 – Итоги регрессии для зависимой переменной регрессионной модели
В результате осталось 4 наиболее значимых факторных признаков: x2 – ностро-счета, (тыс. руб); x7 – основные средства и нематериальные активы, (тыс. руб); x8 – вклады физических лиц, (тыс. руб); x9 – средства предприятий и организаций, (тыс. руб). Проверка статистической значимости и надежности параметров уравнения регрессии, проверялось на основании t-критерия Стьюдента. Все параметры регрессии оказались статистически значимыми и надежными с уровнем значимости 95% , так как их наблюдаемые значения коэффициента по модулю больше табличного значения 2,03. Таким образом, условие было выполнено. Зависимость активов банков ПФО от четырех факторных признаков можно описать следующим уравнением регрессии: 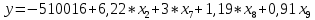 На основании бета-коэффициентов мы можем сделать вывод о силе влияния факторов на результативный признак. Наиболее сильное влияние на сумму активов банков оказывает x2 – ностро-счета, наименьшее влияние оказывает x9 – средства предприятий и организаций, (тыс. руб). Также можем сделать вывод, что при увеличении суммы ностро-счета на 1 тыс. руб активы банков будут увеличиваться на 6,22 тыс. руб, при увеличении основных средств и нематериальных активов на 1 тыс. руб, активы банков будут также увеличиваться на 3 тыс. руб. А сумма активов банков ПФО увеличится на 1,19 тыс. руб, если сумма вкладов физических лиц увеличится на 1 тыс. руб. При увеличении суммы средств предприятий и организаций в банках ПФО на 1 тыс. руб, сумма активов банков увеличится на 0,91 тыс. руб. Далее из исходной модели были исключены факторы с помощью пошагового метода с исключением в программе «Statistika». Таблица итоговых статистик множественной модели регрессии представлена ниже. Таблица 4 – Итоговые статистики модели регрессии
Таким образом, условие достаточности количества наблюдений было выполнено, так как уравнение множественной регрессии было построено по 40 наблюдениям, данное число превышало число объясняющих переменных. Модель более качественна, если коэффициент детерминации приближен к единице. Видим, что у данной модели коэффициент детерминации равен 0,998. Значение данного индекса стремится к 1. Таким образом, вариация переменной y – активы банков ПФО на 99,8% объясняется вариацией пяти факторов. Остальные 0,2% приходятся на другие факторы, не учтенные в модели. Коэффициент корреляции составил 0,997. Связь прямая, сильная, так как находится в соответствующем диапазоне от 0,7 до 1. Точность модели доказывалась с помощью расчета стандартной ошибки оценки. Ошибка была равна 1407730,35, она меньше, чем значение 16248816 – 10% от среднего значения результативного признака, поэтому модель признается точной. Рассчитанное наблюдаемое значение F-критерия Фишера при степенях свободы 5 и 35 составило 2408,67, оно больше его табличного значения 4,4, поэтому уравнение в целом считается статистически значимым и надежным с уровнем значимости 95%. Далее была построена таблица с итогами регрессии для зависимой переменной регрессионной модели. Таблица 5 – Итоги регрессии для зависимой переменной регрессионной модели
В результате осталось 5 наиболее значимых факторных признаков: x3 – выданные МБК, (тыс. руб); x4 – вложения в ценные бумаги (тыс. руб); x5 – кредиты физическим лицам, (тыс. руб); x6 – кредиты предприятиям и организациям, (тыс. руб); x8 – вклады физических лиц, (тыс. руб). Проверка статистической значимости и надежности параметров уравнения регрессии, проверялось на основании t-критерия Стьюдента. Все параметры регрессии оказались статистически значимыми и надежными с уровнем значимости 95% , так как их наблюдаемые значения коэффициента по модулю больше табличного значения 2,032. Таким образом, условие было выполнено. Зависимость активов банков ПФО от пяти факторных признаков можно описать следующим уравнением регрессии: |
