Эконометрические модели формирования финансовых активов кредитных организаций ПФО. Курсовая. Эконометрические модели формирования финансовых активов кредитных организаций пфо
 Скачать 436.93 Kb. Скачать 436.93 Kb.
|
|
Теперь можем заметить, что у всех главных компонент значения критерия информативности больше 60%, они являются оптимальными. Первая компонента нагружена следующими факторами: x2 – ностро-счета, тыс. руб; x3 – выданные МБК, тыс. руб; x4 – вложения в ценные бумаги тыс. руб; х8 – вклады физических лиц, тыс. руб; х9 – средства предприятий и организаций, тыс. руб. Данные принадлежат различным группам показателей, сложно дать обобщенное название первой компоненте, поэтому она была названа как «Депозиты и вложения в ценные бумаги». Следующая вторая компонента нагружена тремя факторами: х6 – кредиты предприятиям и организациям, тыс. руб; х7 – основные средства и нематериальные активы, тыс. руб; х10 – просроченная задолженность по кредитному портфелю, тыс. руб; Компонента «кредиты предприятиям, основные средства и нематериальные активы». Третья компонента состоит из одного факторного признака: х5 – кредиты физическим лицам, тыс. руб. Компонента «кредиты физическим лицам». Ниже представлена таблица с распределением факторов по главным компонентам. Таблица 11 – Состав главных факторных компонент
Таким образом, данные о факторных нагрузках позволили определить набор исходных факторных признаков, которые были определены в три главные компоненты. Наибольший вес в структуре первой факторной компоненты занимают: х3 – выданные МБК с факторной нагрузкой 0,97, х9 – средства предприятий и организаций с нагрузкой 0,967 и х4 – вложения в ценные бумаги с нагрузкой 0,941. В структуре второй компоненты можно выделить фактор с наибольшей факторной нагрузкой 0,913 х6 – кредиты предприятиям и организациям. В третьей компоненте единственный фактор х2 – имеющий факторную нагрузку 0,926 . Далее была построена эконометрическая модель зависимости активов банков от трех главных факторных компонент. При применении пошаговой множественной регрессии с включением и исключением факторов, в обоих случаях значимыми факторными компонентами стали три рассматриваемые: 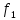 – «депозиты и вложения в ценные бумаги» – «депозиты и вложения в ценные бумаги»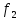 – «кредиты предприятиям, основные средства и нематериальные активы» – «кредиты предприятиям, основные средства и нематериальные активы»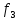 – «кредиты физическим лицам». – «кредиты физическим лицам».Ниже представлена таблица итоговых статистик множественной модели регрессии. Таблица 12 – Итоговые статистики модели регрессии
Условие достаточности количества наблюдений было выполнено, так как уравнение множественной регрессии было построено по 40 наблюдениям, данное число превышало число объясняющих переменных. Модель более качественна, если коэффициент детерминации приближен к единице. У данной модели коэффициент детерминации равен 0,995. Значение данного индекса стремится к 1. Таким образом, вариация переменной y –активы банка на 99,5% объясняется вариацией трех факторных компонент. Остальные 0,5% приходятся на другие факторы, не учтенные в модели. Коэффициент корреляции составил 0,989. Связь прямая, сильная, так как находится в соответствующем диапазоне от 0,7 до 1. Точность модели доказывалась с помощью расчета стандартной ошибки оценки. Ошибка была равна 2 694 015,16, она меньше, чем значение 16 248 815,83 – 10% от среднего значения результативного признака, поэтому модель признается точной. Рассчитанное наблюдаемое значение F-критерия Фишера при степенях свободы 3 и 36 составило 1087,22975, оно больше его табличного значения 8,5, поэтому уравнение в целом считается статистически значимым и надежным с уровнем значимости 95%. Далее была построена таблица с итогами регрессии для зависимой переменной регрессионной модели. Таблица 13 – Итоги регрессии для зависимой переменной регрессионной модели
Проверка статистической значимости и надежности параметров уравнения регрессии, проверялось на основании t-критерия Стьюдента. Все параметры регрессии оказались статистически значимыми и надежными с уровнем значимости 95% , так как их наблюдаемые значения коэффициента по модулю больше табличного значения 2,028. Таким образом, условие было выполнено. Таким образом, зависимость активов банка от трех факторных компонент можно описать следующим уравнением регрессии: 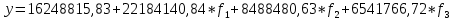 На основании бета-коэффициентов мы можем сделать вывод о силе влияния факторов на результативный признак. Наиболее сильное влияние на сумму активов банка оказывает первая факторная компонента - «депозиты и вложения в ценные бумаги», вторая компонента и третья оказывают меньшее влияние. Затем модель множественной регрессии проверялась на наличие пяти предпосылок МНК или на теорему Гаусса-Маркова.Согласно рисунку 2, представленному ниже, мы увидели, что первая предпосылка о случайном характере остатков не выполняется, так как на графике значения остатков выходят за границы допустимого «коридора», не лежат на одной прямой, то есть остатки представляют собой неслучайные величины. 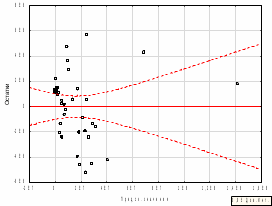 Рисунок 2 – График остатков результативного признака Вторая предпосылка относительно нулевой средней величины остатков тоже не выполняется, так как остатки на графике не лежат на одной прямой и выходят за границы допустимого «коридора», то есть случайное отклонение в среднем оказывает влияние на зависимую переменную и остатки зависимы от значений факторных признаков. 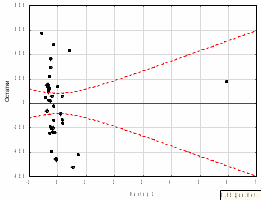 Рисунок 3 – График остатков факторного признака f1  Рисунок 4 – График остатков факторного признака f2 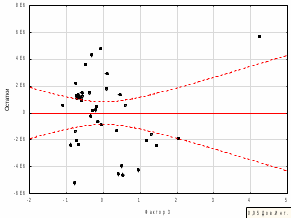 Рисунок 5 – График остатков факторного признака f3 Третья предпосылка о гомоскедастичной дисперсии остатков не выполняется. Если обратиться к рисунку 2, то мы можем увидеть, что дисперсия остатков неоднородна. Наблюдается гетероскедастичность. Четвертая предпосылка – проверка остатков на отсутствие автокорреляции при помощи критерия Дарбина-Уотсона была выполнена. Таблица 14 – Значение критерия Дарбина-Уотсона
При n=40 и k=3 нижняя граница dн=1,34 и верхняя граница dв=1,66. Отсюда получаем, что фактическое значение критерия Дарбина-Уотсона не попадает в зону неопределенности dн < DW < dв, соответственно, присутствует автокорреляция остатков. Пятая предпосылка МНК о нормальном распределении остатков выполняется, так как распределение остатков подобно нормальному, что показывает построенный график нормального распределения. 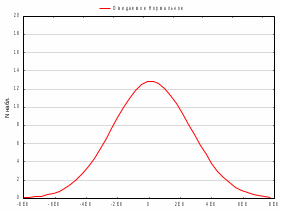 Рисунок 6 – График нормального распределения Таким образом, было проведено исследование модели множественной линейной регрессии по пяти базовым условиям верификации и по пяти предпосылкам метода наименьших квадратов. Так как выполненными оказались все пять базовых условий верификации и выполнена одна последняя предпосылка МНК, можно сделать вывод, что данная модель регрессии подлежит применению на практике для решения исследуемой проблемы, но, чтобы построить достаточно точные дальние прогнозы о величины активов банков ПФО, модель нужно корректировать. 2.3 Построение системы эконометрических уравнений, характеризующих состояние финансовых активов кредитных организаций ПФО Для построения системы уравнений финансовых активов кредитных организаций ПФО были рассмотрены следующие показатели: y1 –активы-нетто (тыс. руб).; y2 – капитал (тыс. руб.).; Для проведения анализа используется следующие экзогенные переменные: x1 – денежные средства в кассе, (тыс. руб); х2 – ностро-счета, (тыс. руб); х3 – выданные МБК, (тыс. руб); х4 – вложения в ценные бумаги (тыс. руб); х5 – кредиты физическим лицам, (тыс. руб); х6 – кредиты предприятиям и организациям, (тыс. руб); х7 – основные средства и нематериальные активы, (тыс. руб); х8 – вклады физических лиц, (тыс. руб); х9 – средства предприятий и организаций, (тыс. руб); х10 – просроченная задолженность по кредитному портфелю, (тыс. руб). Для описания структурных связей была построена СОУ, включающая 2 эндогенные переменные и 10 экзогенных переменных. При отборе переменных во избежание ошибок спецификации модели было принято во внимание то, что для выполнения условия статистической значимости и надежности результатов построения эконометрических моделей количество наблюдений в 3-6 раз должно превышать количество зависимых переменных (наблюдений 40) Для построения системы был использован метод пошагового регрессионного анализа с включением в модель значимых регрессоров. Таким образом, в модели вошли только статистически значимые переменные. Полученная система имеет вид: . 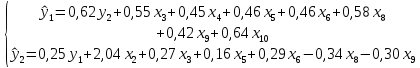 Для оценивания СОУ используется двухшаговый метод МНК. Он дает состоятельные и несмещенные оценки коэффициентов уравнения, является достаточно простым и удобным для вычисления. Использование 2МНК для оценивания структурных коэффициентов модели дает смещенные несостоятельные оценки. Поэтому для определения структурных коэффициентов структурная форма была преобразована в приведенную, которая ничем не отличается от системы независимых переменных, параметры которой оцениваются обычным МНК. Все два уравнения системы были преобразованы в приведенную форму: 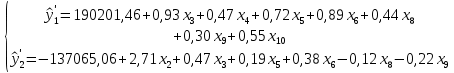 При переходе от приведенной формы модели к структурной возникает проблема идентификации. Идентификация – единственность соответствия между приведенной и структурной формами модели. Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентификацию. Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема. Первое уравнение включает 2 эндогенных переменных (y1, y2). В уравнении отсутствуют 3 экзогенных переменных (x1,x2,x7,). 3+1>1 (D+1>H). Значит уравнение сверхидентифицируемо. Второе уравнение включает 2 эндогенные переменные (y1,y2). В уравнении отсутствуют 4 экзогенные переменные (x1,x4,x7x10). 4+1>3 (D+1>H). Значит уравнение сверхидентифицируемо. Так как все уравнения сверхидентифицируемы, следовательно система сверхидентифицируема. Рассмотренное счетное правило отражает необходимое, но не достаточное условие идентифицируемости. Более точное условие идентификации определяется, если накладывать ограничения на коэффициенты матрицы параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнения системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Поэтому каждое из уравнений было проверено на достаточное условие идентификации. Составим матрицу коэффициентов структурной формы модели. Таблица 15 – Матрица коэффициентов структурной формы модели.
В соответствии с достаточным условием идентификации определить матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы - числу эндогенных переменных минус 1, т.е. 2-1=1. В первом уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
Ранг А1=1, т.к. определитель подматрицы 1х1 матрицы А1 не равен нулю (DefA1*=2,04) Достаточное условие идентификации для первого уравнения выполняется. Во втором уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
Ранг А2=1, т.к. определитель подматрицы 1х1 матрицы А2 не равен нулю (DefA1*=0,45) Достаточное условие идентификации для первого уравнения выполняется. Таким образом, для всех уравнений структурной формы выполняется достаточное условие идентифицируемости. На основе системы приведенных уравнений были получены теоретические значения трех эндогенных переменных. Таким образом, система уравнений приняла следующий вид: 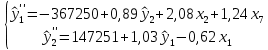 Ниже приведена таблица с итоговыми статистиками структурной формы системы эконометрических уравнений. Таблица 16 – Итоговые статистики структурной формы
Можем заметить, что у первого уравнения коэффициент детерминации равен 0,999. Значение данного индекса близко к 1. Таким образом, вариация переменной y1 – стоимость активов банков на 99,9% объясняется вариацией факторов, включенных в модель. Остальные 0,1% приходятся на другие факторы, не учтенные в модели. Значение коэффициента детерминации второй модели равно 0,989. То есть вариация переменной у2 - капитал банков на 98,9% объясняется вариацией факторов, включенных в эту модель. Коэффициенты корреляции первой модели составили 0,998, второй модели 0,979. Они отражают достаточно тесную связь результативного признака с набором факторных признаков. Точность моделей доказывалась с помощью расчета стандартной ошибки оценки. Ошибка первой и второй модели меньше, чем 10% значения от среднего значения результативного признака, поэтому модель признается точной (1025566,11<1624881,58); (753405,8<1624881,58). Рассчитанные наблюдаемые значения F-критерия Фишера в моделях, больше их табличных значений (3,7; 19,5) соответственно, поэтому уравнения в целом считаются статистически значимыми и надежными с уровнем значимости 95%. Далее по модели регрессии рассматривались итоги регрессии для зависимой переменной. Таблица 17 – Итоги регрессии для зависимой переменной Y1
Таким образом, значимыми факторами в структурной модели регрессии оказались следующие три: y2 – капитал (тыс. руб); х2 – ностро-счета, (тыс. руб); х7 – основные средства и нематериальные активы, (тыс. руб). По данной модели можно сделать следующий вывод. При росте стоимости капитала на единицу тыс. руб при неизменном уровне других показателей стоимость активов увеличится в среднем на 0,89 человек. При увеличении суммы носто-счета на 1 тыс. руб стоимость активов банка увеличится в среднем на 2,08 тыс. руб. С увеличением основных средств и нематериальных активов активы банка возрастут на 1,24 тыс. руб. Ранжирование факторных признаков по степени их влияния на результативный признак проводилось с использованием бета-коэффициентов, были сделаны следующие выводы. Рост стоимости активов в большей степени, зависит от суммы капитала, и в меньшей степени от основных средств и нематериальных активов. Прогнозирование стоимости активов кредитной организации Банк «Йошкар-Ола» методом экспоненциального сглаживания. В настоящее время одним из наиболее перспективных направлений исследования и прогнозирования одномерных временных рядов считаются адаптивные методы. У истоков адаптивных методов находится модель экспоненциального сглаживания. Экспоненциальное сглаживание — один из простейших и распространенных приемов выравнивания ряда. Экспоненциальное сглаживание можно представить как фильтр, на вход которого последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней. Следует иметь в виду, что экспоненциальное сглаживание - это наиболее простой способ построения прогнозов. Часто он даёт быстрые и эффективные результаты. Однако этот метод не позволяет строить доверительные интервалы и, следовательно, рассчитать риски при использовании прогнозов. Рассмотрим прогнозирование с использованием моделей экспоненциального сглаживания. В качестве примера рассмотрим месячные данные о стоимости активов банка «Йошкар-Ола» с январь 2016 г. по январь 2022 г. (Приложение Б) Для моделирования прогноза нам необходимо проверить стационарность временного ряда. Так как стационарность временного ряда означает, что такие компоненты как тренд и сезонность отсутствуют. Говоря более точно, среднее значение и дисперсия не меняются со смещением во времени. Для проверки ряд на стационарность построили график ряда. 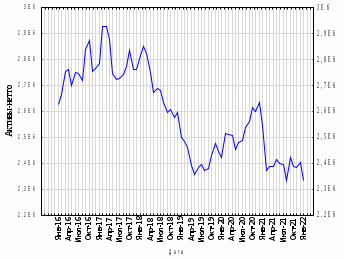 Рисунок 7 – График временного ряда, характеризующего стоимость активов Рисунок 7 – График временного ряда, характеризующего стоимость активовНаблюдаемый ряд не является стационарным, как это хорошо видно на графике. Из графика можно предположить, что в исследуемых данных присутствует линейный возрастающий тренд и сезонная мультипликативная составляющая, следовательно, ряд нестационарен. Признаком стационарности можно считать нормальность распределения остатков ряда. Для этого была построена гистограмма распределения ряда.  Рисунок 8 – Гистограмма распределения остатков исходного временного ряда Из графика видно, что гистограмма распределения остатков плохо подходит к графику нормального распределения. Следовательно, можно предположить, что исходный ряд не является стационарным, и на данном этапе анализа необходимо привести временной ряд к стационарному виду. Для экспоненциального преобразования выберем модель Винтера (модель с линейным мультипликативным трендом), с лаговым значением равным 12. И выполним экспоненциальное сглаживание. В приложении (В) отображенные численные результаты сглаживания и прогноз. Также были выведены стандартные ошибки построенной модели Таблица 18 – Стандартные ошибки построенной модели
В рассмотренном случае процент средней абсолютной ошибки составляет ≈ 1,42% (<13%), что говорит о достаточной точности предложенной модели. Рассмотрим график наблюдаемого временного ряда, сглаженного ряда и остатков. 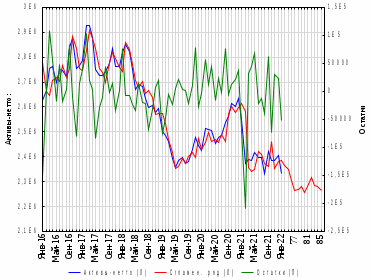 Рисунок 9 – График наблюдаемого временного ряда, сглаженного ряда и остатков Рисунок 9 – График наблюдаемого временного ряда, сглаженного ряда и остатковНа рисунке хорошо просматривается, что значения сглаженного ряда достаточно сильно совпадают с реальными наблюдениями, при этом ряд остатков колеблется около нуля. Из графика (Рис.9) видно, что сглаженные значения ряда повторяют контуры наблюдаемого временного ряда, значения прогнозной линии достаточно близки по структуре к динамике исходного временного ряда, что позволяет сделать вывод об адекватности построенного прогноза реальным данным. Для проверки адекватности прогнозной модели построим гистограмму распределения остатков сглаженного ряда. 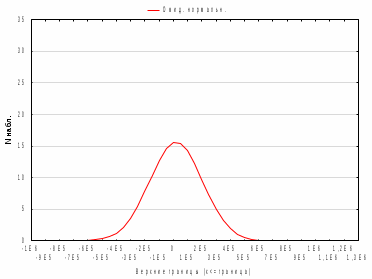 Рисунок 10 – Гистограмма распределения остатков сглаженного ряда Рисунок 10 – Гистограмма распределения остатков сглаженного рядаИз графика видно, что гистограмма распределения остатков сглаженного ряда подобна графику нормального распределения, следовательно, можно сделать вывод, что построенная модель адекватно отражает наблюдаемый процесс динамики стоимости активов банка «Йошкар-Ола» и построенный на её основе прогноз можно считать точным. Для проверки адекватности модели необходимо оценить автокорреляционную функцию и частную автокорреляционную функции остатков, а также плотность распределения остатков. 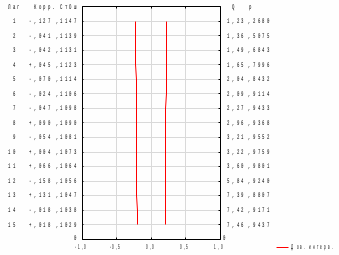 Рисунок11 – График автокорреляционной функции остатков Рисунок11 – График автокорреляционной функции остатков (после преобразований графика) Анализ значений автокорреляционной функции остатков показывает, что ряд остатков похож на белый шум. 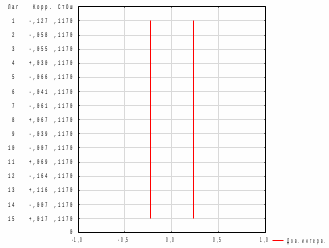 Рисунок 12 – График частной автокорреляционной функции остатков Анализ частной автокорреляционной функции также показывает отсутствие сильных взаимосвязей уровней остаточного ряда. Так как процент ошибки равен 1,42 (<13% - допустимый предел), анализ автокорреляционной и частной автокорреляционной функций доказывает отсутствие сильных взаимосвязей уровней остаточного ряда, плотность распределения остатков близка к плотности нормального распределения можно сделать вывод о достаточно хорошем подборе прогнозной модели. Следовательно, используя полученную модель, можно строить прогноз. Заключение Таким образом, в ходе курсовой работы была достигнута ее цель, при помощи многомерных статистических методов анализа были построены эконометрические модели финансовых активов кредитных организаций ПФО. А также были выполнены все поставленные задачи. Рассмотрели теоретические аспекты кредитных организация и формирования финансовых активов, также было проведено моделирование показателя стоимости активов кредитных организаций ПФО по главным компонентам. Финансовые активы — это ресурсы, контролируемые организацией, использование которых возможно вызовет в будущем приток экономической выгоды. Размещение средств организации имеет огромное значение и в повышении эффективности финансовой деятельности. От того, какие средства вложены в основные и оборотные средства, сколько их находится в сферах производства и обращения, в денежной и материальной форме, насколько оптимально их соотношение, во многом зависят результаты производственной и финансовой деятельности, и, следовательно, и финансовое состояние организации. Можно сказать, что на стоимость активов кредитных организаций Приволжского федерального округа влияют финансовые показатели: x3 – выданные межбанковские кредиты; x4 – вложения в ценные бумаги; x5 – кредиты физическим лицам; x6 – кредиты предприятиям и организациям; x8 – вклады физических лиц. А на основании бета-коэффициентов мы можем сделать вывод о силе влияния факторов на результативный признак. Наиболее сильное влияние на сумму активов банков оказывает два фактора x3 – выданные МБК и x6 – кредиты предприятиям и организациям. Наименьшее влияние оказывает фактор x8 – вклады физических лиц. рабочей силы определенно влияют социально-экономические факторы. В ходе работы были построены три эконометрические модели, отражающие зависимость активов от предложенных показателей. В ходе исследования было выяснено, что тремя главными факторными компонентами, влияющими на исследуемый показатель стали следующие: 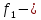 «депозиты и вложения в ценные бумаги». «депозиты и вложения в ценные бумаги».Включает в себя: x2 – ностро-счета, тыс. руб; x3 – выданные МБК, тыс. руб; x4 – вложения в ценные бумаги тыс. руб; х8 – вклады физических лиц, тыс. руб; х9 – средства предприятий и организаций, тыс. руб. Следующая вторая компонента 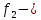 кредиты предприятиям, основные средства и нематериальные активы» нагружена тремя факторами: кредиты предприятиям, основные средства и нематериальные активы» нагружена тремя факторами:х6 – кредиты предприятиям и организациям, тыс. руб; х7 – основные средства и нематериальные активы, тыс. руб; х10 – просроченная задолженность по кредитному портфелю, тыс. руб; Третья компонента 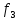 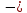 «кредиты физическим лицам»состоит из одного факторного признака: «кредиты физическим лицам»состоит из одного факторного признака:х5 – кредиты физическим лицам, тыс. руб. Наиболее сильное влияние на сумму активов банка оказывает первая факторная компонента - «депозиты и вложения в ценные бумаги», вторая компонента и третья оказывают меньшее влияние. Также была построена система эконометрических уравнений, отражающая зависимость между финансовыми показателями и двумя результативными признаками, характеризующие финансовые активы банков: y2 – капитал (тыс. руб); х2 – ностро-счета, (тыс. руб); х7 – основные средства и нематериальные активы, (тыс. руб). По данной модели можно сделать следующий вывод. При росте стоимости капитала на единицу тыс. руб при неизменном уровне других показателей стоимость активов увеличится в среднем на 0,89 человек. При увеличении суммы носто-счета на 1 тыс. руб стоимость активов банка увеличится в среднем на 2,08 тыс. руб. С увеличением основных средств и нематериальных активов активы банка возрастут на 1,24 тыс. руб. Ранжирование факторных признаков по степени их влияния на результативный признак проводилось с использованием бета-коэффициентов, были сделаны следующие выводы. Рост стоимости активов в большей степени, зависит от суммы капитала, и в меньшей степени от основных средств и нематериальных активов. Список литературы Батищева Г.А., Терехов Н.А. Исследование влияния макроэкономических факторов на эффективность деятельности кредитных организаций [Текст] / Батищева Г.А., Терехов Н.А. – Вестник РГЭУ РИНХ. – 2017. – №3 (59). Бекарева С.В., Мельтенисова Е.Н. Факторы прибыльности российского банковского сектора [Текст] / Бекарева С.В., Мельтенисова – Вестник ОмГУ. Серия: Экономика. – 2018. – №4. Босенко Я.В. Развитие организационно-методического обеспечения учета финансовых результатов деятельности экономического субъекта: дис. на соискание ученой степени канд. экон. наук. [Текст] // Ставрополь. – 2018. – 182с. Горяинова Е.Р. Прикладные методы анализа статистических данных: Учебное пособие / Е.Р. Горяинова, А.Р. Панков, Е.Н. Платонов. — М.: ИД ГУ ВШЭ, 2018. — 310 c. Жуков Е. Ф. Банки и небанковские кредитные организации, и их операции: [Текст] / Е. Ф. Жуков – Москва: Юнити-Дана, 2017. – 559с. Зубов С.А. Финансовые результаты банковского сектора в 2021г. [Текст] / Зубов С.А. – Экономическое развитие России. – 2022. – №2. Инструкция Банка России от 21 июня 2018 г. N 188-И "О порядке применения к кредитным организациям (головным кредитным организациям банковских групп) мер, предусмотренных статьей 74 Федерального закона "О Центральном банке Российской Федерации (Банке России)" (с изменениями и дополнениями) [Электронный ресурс] – https://base.garant.ru/72029492/ (Дата обращения: декабрь 2022). Информационный портал banki.ru [Электронный ресурс] / Рейтинги банков - Электрон, дан. - 2018.- Режим доступа: http://www.banki.ru/ banks/ratings/, свободный. - Загл. с экрана. - Яз. рус. - дата обращения: декбрь 2022. Катаргин Н.В. Экономико-математическое моделирование: учебное пособие / Н.В. Катаргин. – СПб.: Издательство Лань, 2018. - 256 c. Колпаков В.Ф. Экономико-математическое и эконометрическое моделирование: Компьютерный практикум: Учебное пособие / В.Ф. Колпаков. – М.: Инфра-М, 2018. - 672 c. Куликов Е.И. Прикладной статистический анализ. 2-е изд.,/ Е.И. Куликов. — М.: ГЛТ, 2018. — 464 c. Марамыгин М. С., Прокофьева Е. Н. Деньги, кредит, банки: учебное пособие [Текст] / М. С. Марамыгин, Е. Н. Прокофьева – Екатеринбург: Изд-во Урал. Ун-та. 2019. – 384 c. О банках и банковской деятельности: Федеральный закон от 02.12.1990 г. № 395-1-ФЗ [Электронный ресурс] – http:// ivo.garant.ru/#/document/10105800/paragraph/990967/highlight/ (дата обращения: 20.05.2022). Положение Банка России от 22 декабря 2014 г. N 446-П "О порядке определения доходов, расходов и прочего совокупного дохода кредитных организаций" (с изменениями и дополнениями) [Электронный ресурс] – https://base.garant.ru/70832382/ (Дата обращения: декабрь 2022). Указание Банка России от 3 апреля 2017 г. N 4336-У "Об оценке экономического положения банков" (с изменениями и дополнениями) [Электронный ресурс] – https://base.garant.ru/71682362/ (Дата обращения: декабрь 2022). Федеральный закон от 10 июля 2002 г. N 86-ФЗ "О Центральном банке Российской Федерации (Банке России)" (с изменениями и дополнениями) [Электронный ресурс] – https://base.garant.ru/12127405/ (Дата обращения: декабрь 2022). Чеботарева Г.С. Организация деятельности коммерческого банка: учебное пособие [Текст] / Чеботарева Г. С. – Екатеринбург: Издательство Уральского университета, 2018. — 120 с. Шершнева Е.Г. Диагностика финансового состояния коммерческого банка: учебно-методическое пособие [Текст] / Е.Г. Шершнева – Екатеринбург: Издательство Уральского университета, 2017. — 112с. Шелкунова Т.Г., Шеина Е.С. Особенности оценки финансовых результатов и эффективности деятельности коммерческого банка [Текст] / Шелкунова Т.Г., Шеина Е.С. – Экономика и бизнес: теория и практика. 2018. №4. Юзвович Л. И., Мокеева Н. Н., Слепухина Ю. Э., Бакунова Т. В., Заборовская А. Е., Чеботарева Г. С. Банковское дело: учебное пособие [Текст] / Л. И. Юзвович, Н. Н. Мокеева, Ю. Э. Слепухина, Т. В. Бакунова, А. Е. Заборовская, Г. С. Чеботарева – Екатеринбург: Издательство Уральского университета, 2020. – 296 с. Приложения Приложение А Исходные данные для факторного анализа
Приложение Б Показатели деятельности банка «Йошкар-Ола» за период c 01.01.2016 по 01.01.2022 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

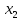 - ностро-счета, тыс. руб;
- ностро-счета, тыс. руб;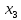 - выданные МБК, тыс. руб;
- выданные МБК, тыс. руб;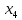 - вложения в ценные бумаги тыс. руб;
- вложения в ценные бумаги тыс. руб;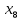 - вклады физических лиц, тыс. руб;
- вклады физических лиц, тыс. руб;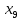 - средства предприятий и организаций, тыс. руб.
- средства предприятий и организаций, тыс. руб. - кредиты предприятиям и организациям, тыс. руб;
- кредиты предприятиям и организациям, тыс. руб;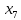 - основные средства и нематериальные активы, тыс. руб;
- основные средства и нематериальные активы, тыс. руб;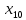 - просроченная задолженность по кредитному портфелю, тыс. руб;
- просроченная задолженность по кредитному портфелю, тыс. руб;