Практическая ЭММ. Практическая работа ЭММ. Экономикоматематические методы
 Скачать 37.83 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ В ЛОГИСТИК____ Группа Студент МОСКВА 2022 СОДЕРЖАНИЕ: Практическое занятие 1. Методы составления первоначального плана поставок. Метод северо-западного угла. Задача 1…………………………………………………………………..3 Практическое занятие 1. Методы составления первоначального плана поставок. Метод минимальной стоимости. Задача 2…………………………………………………………………..5 Практическое занятие 1. Методы составления первоначального плана поставок. Особый случай построения первоначального плана поставок. Задача 3…………………………………………………………………..6 Практическое занятие 2. Методы решения транспортной задачи. Матрица оценок. Задача 1………………………………………………….………………8 Практическое занятие 2. Методы решения транспортной задачи. Метод оптимизации первоначального плана поставок. Задача 2………………………………………………………………….10 Практическое занятие 1. Методы составления первоначального плана поставок. Метод северо-западного угла. Задача 1. Найти первоначальный план поставок методом северо-западного угла для данных представленных в таблице. Вычислить значение целевой функции.
Решение: Стоимость перевозок единицы груза от поставщиков к потребителям задается матрицей коэффициентов затрат: С = 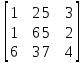 Определим суммарную мощность поставщиков: 𝑀 = 60 + 120 +100 = 280 единиц. Определим суммарный спрос потребителей: 𝑁 = 20 + 110 + 40 + 110 =280 единиц. Поскольку 𝑀 = 𝑁, то экономико-математическая модель транспортной задачи является закрытой. Запишем исходные данные в виде таблицы поставок:
Вычислим значение целевой функции для полученного первоначального плана поставок транспортной задачи по формуле: F = 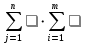 cij ⋅ xij= 1×20 +2×40+6×70+5×40+2×10+ 4×100 =1170 д.е. Ответ: суммарные затраты на перевозку груза от поставщиков к потребителям по плану поставок, полученному методом северо-западного угла, равняются 1170 у.е. Практическое занятие 1. Методы составления первоначального плана поставок. Метод минимальной стоимости. Задача 2. Найти первоначальный план поставок методом минимальной стоимости для данных представленных в задаче 1. Вычислить значение целевой функции.
Решение. В этом методе на каждом шаге решения поставка осуществляется в клетку с наименьшей стоимостью перевозки единицы груза среди всех незаполненных клеток.
Вычислим значение целевой функции для полученного первоначального плана поставок транспортной задачи по формуле: F = 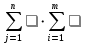cij ⋅ xij= 1×20+2×40+5×40+2×100+3×70 =710 д.е. Ответ: Видим, что суммарные затраты на перевозку груза от поставщиков к потребителям по плану поставок, полученному методом минимальной стоимости равны 710 у.е., что на 460 у.е. меньше, чем в методе северо- западного угла (1170у.е.). Практическое занятие 1. Методы составления первоначального плана поставок. Особый случай построения первоначального плана поставок. Задача 3. У поставщиков 𝐴1, 𝐴2, 𝐴3 сосредоточено соответственно 80, 30, 50 единиц некоторого однородного груза. Этот груз необходимо доставить потребителям 𝐵1, 𝐵2, 𝐵3 в количестве 20, 60 и 80 единиц соответственно. Стоимость перевозок единицы груза от поставщиков к потребителям задается матрицей коэффициентов затрат С= 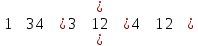 Необходимо построить первоначальный план поставок методом северо- западного угла и вычислить их суммарную стоимость. Решение. Рассмотрим алгоритм решения. Шаг 1. Для клетки (1,1): 𝑥11 = min (𝑀1,𝑁1 )= min (80, 20) = 20. Исключаем из решения первый столбец. Шаг 2. Для клетки (1,2): 𝑥12 = min (𝑀1,𝑁2) = min (80 – 20, 60) = 60. Исключаем из решения второй столбец и первую строку одновременно. Поэтому в первой строке или во втором столбце одну пустую клетку надо перевести в отмеченные с нулевым объемом поставок. Далее решение задачи производится по обычной схеме. Окончательно получаем следующую таблицу поставок:
Суммарную стоимость всех поставок вычислим по формуле: F = 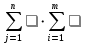cij ⋅ xij= 1×20+3×60+2×30+2×50=360 д.е.Ответ : 360 д.е. Практическое занятие 2. Методы решения транспортной задачи. Матрица оценок. Задача 1. С помощью матрицы оценок исследовать на оптимальность план поставок:
Решение: Вычислим потенциалы всех базисных клеток по формуле: Сiut = Uit + Vut где Сiut – тариф U1+V1 = 1 U2+V1 = 4 U2+V2 = 6 U2+V3 = 5 U3+V3 = 6 U3+V4 = 4 Находим значение потенциалов: U1=0 V1=1 U2=3 V2=3 U3=4 V3=2 V4= 0 Вычислим потенциалы всех небазисных клеток по формуле: dijt = Cij – (Ui + Vj) d12= C12 – (U1 + V1) = 2-(0+3) = -1 d13= C13 – (U1 + V3) = 5-(0+2) = 3 d14= C14 – (U1 + V4) = 3-(0+0) = 3 d24= C24 – (U2 + V4) = 2-(3+0) = -1 d31= C31 – (U3 + V1) = 6-(4+1) = 1 d32= C32 – (U3 + V2) = 3-(4+3) = -4 Получаем матрицу: C= 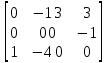 Заполним таблицу:
Ответ: Поскольку матрица оценок содержит отрицательные числа, то план поставок не является оптимальным. Практическое занятие 2. Методы решения транспортной задачи. Метод оптимизации первоначального плана поставок. Задача 2. С помощью распределительного метода найти оптимальный план поставок, используя первоначальный план (таблица).
Решение: 1.Вычислим потенциалы всех базисных клеток по формуле: Сiut = Uit + Vut где Сiut – тариф U1+V1 = 1 U2+V1 = 4 U2+V2 = 6 U2+V4 = 2 U3+V2 = 3 U3+V3 = 6 2.Находим значение потенциалов: U1=0 V1=1 U2=3 V2=3 U3=0 V3=6 V4= -1 3.Вычислим потенциалы всех небазисных клеток по формуле: dijt = Cij – (Ui + Vj) d12= C12 – (U1 + V1) = 2-(0+3) = -1 d13= C13 – (U1 + V3) = 5-(0+6) = -1 d14= C14 – (U1 + V4) = 3-(0+(-1)) = 4 d23= C23 – (U2 + V3) = 5-(3+6) = -4 d31= C31 – (U3 + V1) = 6-(0+1) = 5 d34= C34 – (U3 + V4) = 4-(0+(-1)) = 5 Получаем матрицу: C= 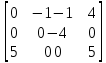 Поскольку матрица оценок содержит отрицательные числа, то план поставок не является оптимальным. Проведём его оптимизацию распределительным методом. Заполняем таблицу:
Построим 1 цикл пересчета. Клетка (1:2). (1:2 +) – (1:1 -) – (2:1 +) – (2:2 -) – (1:2 +) min (-) = 20, тогда проставим новые значения в таблице:
Вычислим потенциалы всех базисных клеток по формуле: Сiut = Uit + Vut где Сiut – тариф U1+V1 = 1 U1+V2 = 2 U2+V1 = 4 U2+V4 = 2 U3+V2 = 3 U3+V3 = 6 Находим значение потенциалов: U1=0 V1=1 U2=3 V2=2 U3=1 V3=5 V4= -1 Вычислим потенциалы всех небазисных клеток по формуле: dijt = Cij – (Ui + Vj) d13= C13 – (U1 + V3) = 5-(0+5) = 0 d14= C14 – (U1 + V4) = 3-(0+(-1)) = 4 d22= C22 – (U2 + V2) = 6-(3+2)= 1 d23= C23 – (U2 + V3) = 5-(3+5) = -3 d31= C31 – (U3 + V1) = 6-(1+1) = 4 d34= C34 – (U3 + V4) = 4-(1+(-1)) = 0 Получаем матрицу: С= 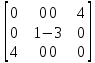 Первая итерация закончилась. Поскольку матрица оценок содержит отрицательные числа, то план поставок цикла пересчета для клетки (1:2) не является оптимальным. Построим 2 цикл пересчета. Клетка (2:3). (2:3 +) – (2:2 -) – (3:2 +) – (3:3 -) – (2:3 +) min (-) = 20, тогда проставим новые значения в таблице:
Вычислим потенциалы всех базисных клеток по формуле: Сiut = Uit + Vut где Сiut – тариф U2+V1 = 4 U2+V3 = 5 U2+V4 = 2 U3+V2 = 3 U3+V3 = 4 Вычислим потенциалы всех небазисных клеток по формуле: dijt = Cij – (Ui + Vj) d12= C12 – (U1 + V2) = 2-(0+1) = 1 d13= C13 – (U1 + V3) = 5-(0+2) = 3 d14= C14 – (U1 + V4) = 3-(0+(-1)) = 4 d22= C22 – (U2 + V2) = 6-(3+1) = 2 d31= C31 – (U3 + V1) = 6-(3+1) = 2 d34= C34 – (U3 + V4) = 4-(3+(-1)) = 2 С= 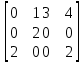 Полученная матрица оценок указывает на то, что новый план поставок является оптимальным. Вычислим значение целевой функции для транспортной задачи по формуле: F = 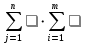cij ⋅ xij= 1×70+4×20+5×20+2×120+3х110+6х120=1550 д.е.Ответ: план поставок цикла пересчета для клетки (2:3) является оптимальным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||