письменная работа. Экономико-математические методы и модели в логистике. Найти первоначальный план поставок методом северозападного угла для данных представленных в таблице. Вычислить значение целевой функции
 Скачать 150.03 Kb. Скачать 150.03 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ __Экономико-математические методы и модели в логистике__ Группа Го19М471_ Студент С.П. Маяренко МОСКВА 2021_ Задача 1. Найти первоначальный план поставок методом северо-западного угла для данных представленных в таблице. Вычислить значение целевой функции.
Решение. Определим суммарную мощность поставщиков 𝑀= 60 +120 + 100= =280 (единиц). Определим суммарный спрос потребителей 𝑁=20+110+40+110= 280 (единиц). 𝑥11 = min 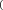 𝑀1, 𝑁1 𝑀1, 𝑁1  = min (60,20) =20; = min (60,20) =20;𝑥12 = min 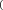 𝑀1, 𝑁2 𝑀1, 𝑁2  = min (60-20,110) =40; = min (60-20,110) =40;𝑥22 = min 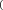 𝑀2, 𝑁2 𝑀2, 𝑁2  = min (120-40,110) =70; = min (120-40,110) =70;𝑥23 = min 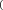 𝑀2, 𝑁3 𝑀2, 𝑁3  = min (120-70,40) =40; = min (120-70,40) =40;𝑥24 = min  𝑀2, 𝑁4 𝑀2, 𝑁4  = min (120-70-40,110) =10; = min (120-70-40,110) =10;𝑥34 = min  𝑀3 𝑁4 𝑀3 𝑁4  = min (100,110-10) =100. = min (100,110-10) =100.  Х = Х =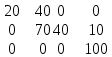 ; ;6 = 3+4-1 – правило соблюдается. nm F=∑∑cij⋅ xij=1×20+2×40+6×70+5×40+2×10+4×100 =1140. j=1 i=1 Ответ: суммарные затраты на перевозку груза от поставщиков к потребителям по плану поставок, полученному методом северо-западного угла, равняются 1140 у.е. Задача 2. Найти первоначальный план поставок методом минимальной стоимости для данных представленных в задаче 1. Вычислить значение целевой функции.
Решение: 𝑥21 = min 𝑀, 𝑁1 = min (120,20) =20; 𝑥12 = min 𝑀1, 𝑁2= min (60,110) = 60; 𝑥24 = min 𝑀2, 𝑁4= min (110,120 – 20) = 100; 𝑥32= min 𝑀3, 𝑁2= min (100,110 – 60) = 50; 𝑥34= min 𝑀3, 𝑁4= min (100 – 50, 110 – 100) = 10; 𝑥33= min 𝑀3, 𝑁3= min (100 – 50, 40) = 40;   Х = Х =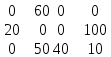 ; ;6 = 3+4-1 – правило соблюдается. nm F=∑∑cij⋅ xij=2×60+1×20+2×100+3×50+7×40+4×10 =810 j=1 i=1 Ответ: минимальной стоимости поставки равна 810 у.е. Задача 3. У поставщиков 𝐴!, 𝐴!, 𝐴! сосредоточено соответственно 80, 30, 50 единиц некоторого однородного груза. Этот груз необходимо доставить потребителям 𝐵!, 𝐵!, 𝐵! в количестве 20, 60 и 80 единиц соответственно. Стоимость перевозок единицы груза от поставщиков к потребителям задается матрицей коэффициентов затрат
Необходимо построить первоначальный план поставок методом северо-западного угла и вычислить их суммарную стоимость. Решение:
𝑥11 = min M1, 𝑁1 = min (80,20) =20; 𝑥12 = min M1, 𝑁2 = min (80 – 20,60) =60; 𝑥22 = min M2, 𝑁2 = 0; 𝑥23 = min M2, 𝑁3 = min (30,80) =30; 𝑥33 = min M3, 𝑁3 = min (50,80) =50. n m F=∑∑cij ⋅ xij =1×20+3×60+1×0+2×30+2×50 =360 j=1 i=1 Ответ: суммарная стоимость всех поставок составила 360 у.е. Задача 1. С помощью матрицы оценок исследовать на оптимальность план поставок
Решение: 𝑥11 = 0 = 0 + а + 1; а = -1 𝑥21 = 0 = -1 + b+ 4; b = -3 𝑥22 = 0 = -3 + c + 6; с = -3 𝑥23 = 0 = -3 +d +5; d = -2 𝑥33 = 0 = e + (-2) + 6; е = -4 𝑥34 = 0 = -4 +f +4; f = 0 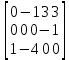 – не является оптимальной. – не является оптимальной.Задача 2. С помощью распределительного метода найти оптимальный план поставок, используя первоначальный план (таблица).
Решение: 𝑥11 = 0 = 0 + а + 1; а = -1 𝑥21 = 0 = b+ (-1) + 4; b = -3 𝑥22 = 0 = -3 + c + 6; с = -3 𝑥32 = 0 = -3 +d +3; d = 0 𝑥33 = 0 = 0 + 6; е = -6 𝑥24 = 0 = -3 +f 2; f = 1 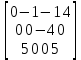 (2,3)→(3,3) →(3,2) →(2,2) →(2,3)
𝑥11 = 0 = 0 + а + 1; а = -1 𝑥21 = 0 = b + (-1) + 4; b = -3 𝑥23 = 0 = -3 + е + 5; е = -2 𝑥24 = 0 = -3 +f +2; f= 1 𝑥33 = 0 = -2+ d+ 6; d = -4 𝑥32 = 0 = -4 +c+3; c = 1 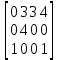 – является оптимальной. – является оптимальной. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||













































 -
-

