Математика готовые вопросы. Математика. Экзаменационные вопросы Множества, операции над множествами. Символика математической логики. Действительные числа и их свойства
 Скачать 2.32 Mb. Скачать 2.32 Mb.
|
|
Математика Экзаменационные вопросы: 1. Множества, операции над множествами. Символика математической логики. Действительные числа и их свойства. 2. Понятие окрестности точки. Предельные, граничные и внутренние точки множества. Открытые и замкнутые множества. Отрезок, интервал, промежуток действительной прямой. Ограниченные множества. 3. Понятие функции. Способы задания функции. Обратная функция, сложная функция. 4. Числовые последовательности. Ограниченность, монотонность и сходимость последовательности. Теоремы о свойствах сходящихся последовательностей. Число e. Понятие предела функции по Коши и по Гейне. 5. Теоремы о пределах для функций. Односторонние пределы. Бесконечно большие, бесконечно малые и эквивалентные величины, – символика. 6. Основные виды неопределенностей. Замечательные пределы. Непрерывность функции в точке и на множестве. 7. Теоремы о свойствах функции, непрерывной в точке. Теоремы о свойствах функции, непрерывной на отрезке. Точки разрыва и их классификация. 8. Производная и дифференциал функции. Геометрический и механический смысл производной. 9. Геометрический смысл дифференциала. Связь с непрерывностью. 10. Понятие дифференцируемости функции, необходимое и достаточное условие дифференцируемости. 11. Правила дифференцирования и формулы производной конкретных функций. Производные высших порядков. 12. Дифференциалы высших порядков. Дифференцирование сложной функции, функции, заданной неявно и параметрически. 13. Теоремы Ферма, Ролля, Лагранжа, Коши. 14. Формула Тейлора. 15. Исследование функции, построение ее графика на основе полного исследования. 16. Производная и дифференциал функции. Геометрический и механический смысл производной. Геометрический смысл дифференциала. 17. Связь с непрерывностью. Понятие дифференцируемости функции, необходимое и достаточное условие дифференцируемости. 18. Правила дифференцирования и формулы производной конкретных функций. Понятие функции нескольких переменных, предел, непрерывность. 19. Определение частных производных. Дифференцируемость функции нескольких переменных в точке. 20. Связь понятий «непрерывность», «существование частных производных», «дифференцируемость в точке». 21. Достаточные условия дифференцируемости. Частные производные и дифференциалы высших порядков. 22. Формула Тейлора. Неявное задание функции. Представление ее по формуле Тейлора. Локальный экстремум. 23. Необходимые и достаточные условия существования. Критерий Сильвестра. Абсолютный экстремум функции нескольких переменных на замкнутой и ограниченной области. Ответы: 1.         2.   3.    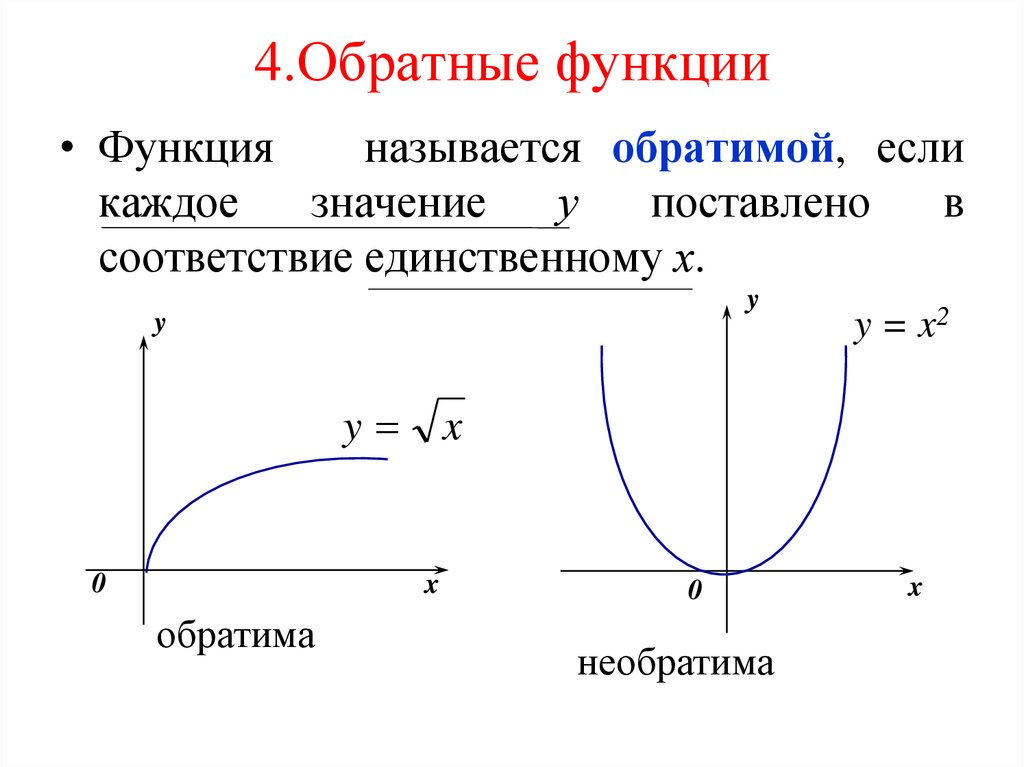  4. 5. 6.    7. 8. 9.   10. 11. 12. 13. 14.   15.     16. 17. 18. 19. 20. 21. 22. 23. |
