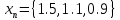Ответы на экзамен. Ответы на экзаменэ. Экзаменационные вопросы по дисциплине Цифровая обработка сигналов
 Скачать 2.67 Mb. Скачать 2.67 Mb.
|
|
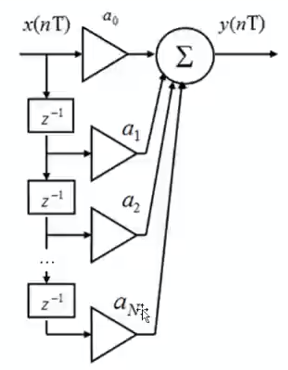
У рекурсивных фильтров ИХ является бесконечной поэтому их называют БИХ-фильтрами. Если коэффициент в цепи обратной связи будет больше единицы, может образоваться положительная обратная связь, фильтр может завестись, и сигнал на его выходе может продолжаться и усиливаться даже после выключения входного воздействия, Задержка на один такт означает, что берётся предыдущий отчёт сигнала. Задержка на один шаг является элементом памяти. Это такой элемент, который получает на вход значение и возвращает значение, которое находится до него. Он хранит отчёты сигнала и при необходимости их выдаёт. У рекурсивного фильтра две линии задержки. Коэффициенты, расположенные в числителе это коэффициенты не рекурсивной части. Коэффициенты в знаменателе — это коэффициенты рекурсивной части. 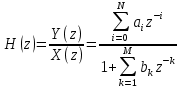 В соответствии с каким алгоритмом осуществляется обработка сигнала нерекурсивным цифровым фильтром? Какой объём вычислительных операций выполняется в нерекурсивном фильтре при обработке одного отсчёта сигнала? Какие способы описания цифровых фильтров вы знаете? Характеристики цифрового фильтра: АЧХ, ФЧХ, ИХ, ПФ, групповая задержка, фазовая задержка.
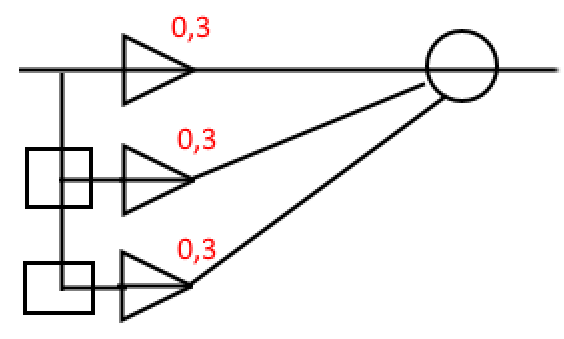
Данную структурную схему можно представить в виде уравнения: 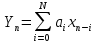 Нерекурсивный фильтр не имеет обратной связи, его выходной сигнал определяется взвешенной с весами al суммой текущего и N (порядок фильтра) предыдущих отсчётов входного сигнала. Нерекурсивные фильтры имеют конечную ИХ поэтому их называют так же КИХ-фильтрами. Нерекурсивные фильтры являются устойчивыми. У нерекурсивного фильтра одна линия задержки. Коэффициенты, расположенные в числителе это коэффициенты не рекурсивной части. Коэффициенты в знаменателе — это коэффициенты рекурсивной части. 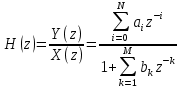 Описание схемы нужно смотреть в предыдущем вопросе (5). Как аналитически могут быть найдены отклики рекурсивного и нерекурсивного фильтров на заданное входное воздействие?
Рис. на входе x = 1.5
Рис. на входе x = 1.1
Рис. на входе x = 0.5
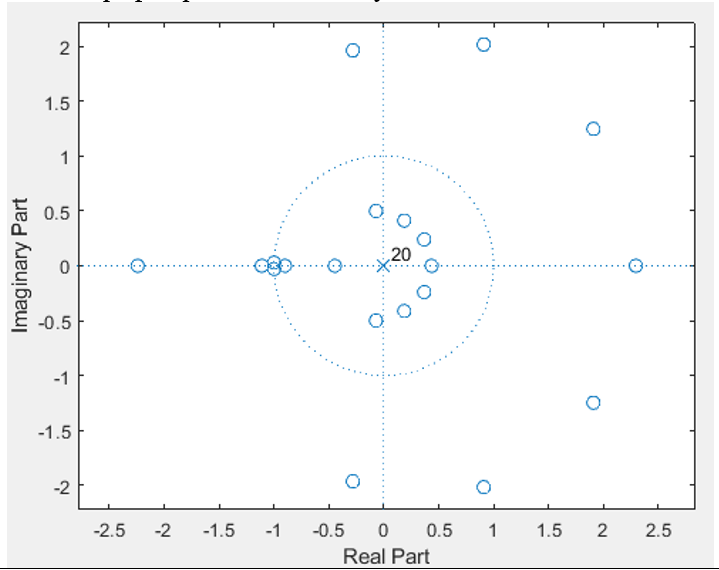
Как определяется импульсная характеристика цифрового фильтра, какие цифровые фильтры называют фильтрами БИХ и КИХ-типа? Какой смысл имеют коэффициенты цифровых фильтров? Импульсная характеристика фильтра — это выходная последовательность фильтра во временной области при подаче на вход фильтра дельта-функции, или функции Дирака — единственного отсчёта, равного единице (единичного импульса), которому предшествуют и за которым следуют нулевые отсчёты. ИХ это реакция на цифровую дельта функцию. Коэффициенты КИХ-фильтра (нерекурсивного) также называют его импульсной характеристикой. Характеристики фильтра можно разделить на временные и частотные. Временные характеристики — это реакция фильтра на какой-то сигнал строго определённой формы. Типовые последовательности для определения характеристик фильтров: Единичный импульс. Цифровая дельта функция. Результатом подачи этого сигнала является на выходе ИХ. Импульсная характеристика – это реакция фильтра на единичный импульс. У нерекурсивного фильтра ИХ представляет собой коэффициенты, выстроившиеся в ряд. У рекурсивного фильтра ИХ длинная и иногда бесконечна из-за рекурсии и из-за того, что алгоритм сложнее чем у нерекурсивного фильтра. За счёт бесконечной ИХ рекурсивный фильтр при одном и том же порядке фильтра имеет лучшее характеристики чем нерекурсивный фильтр. 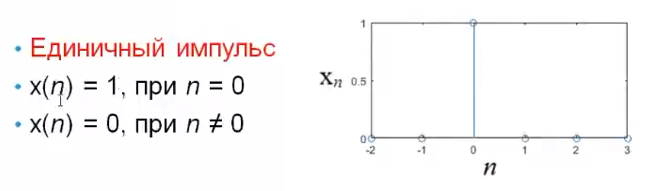 Единичный скачок. Этот сигнал используется для того, чтобы увидеть какова будет реакция на изменения постоянной составляющей. 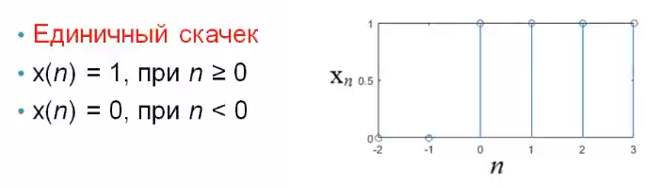 Гармонический сигнал. Дискретная синусоида используется для исследования АЧХ. 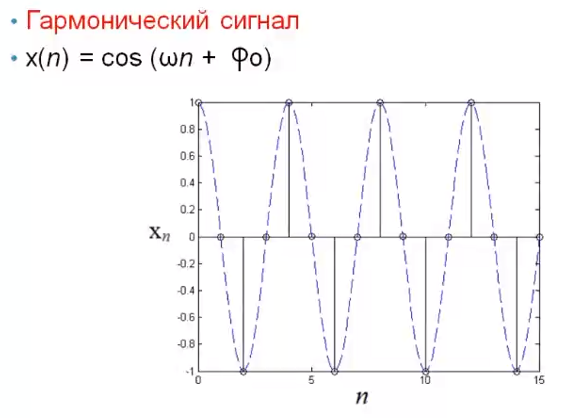 Нерекурсивные фильтры имеют конечную ИХ поэтому их называют так же КИХ-фильтрами. Нерекурсивные фильтры являются устойчивыми. У рекурсивных фильтров ИХ является бесконечной поэтому их называют БИХ-фильтрами. Любой цифровой фильтр работает во временной области. Коэффициенты фильтра перемножаются с отчётами сигнала и таким образом получается выходной сигнал. АЧХ зависит как от коэффициентов фильтра, при изменении хотя бы одного коэффициента приведёт к изменению АЧХ фильтра. Существует жёсткая связь между АЧХ фильтра и его коэффициентами. Как определяются передаточная функция и амплитудно-частотная характеристика цифрового фильтра? Какова их связь с его импульсной характеристикой цифрового фильтра? Передаточная функция H(z) дискретной цепи определяется как отношение z-преобразований выходной и входной последовательностей: 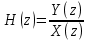 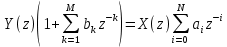 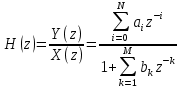 АЧХ это соотношение между амплитудами. Амплитуда выходного сигнала в соответствии с частотой сравнивается с амплитудой входного сигнала на этой же заданной частоте. Можно сказать так: Фурье-образ сигнала на выходе соотносится с Фурье-образом сигнала на входе. АЧХ – это соотношение амплитуды на выход к амплитуде сигнала на входе. АЧХ связана с передаточной функцией. Передаточная функция определяется как отношение z-преобразований выходного и входного сигналов. Для того, чтобы из передаточной функции H(z) получить АЧХ и ФЧХ фильтра, надо вычислить значения модули (для АЧХ) и аргумента (для ФЧХ) передаточной функции для точек, лежащих на оси вещественных частот 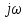 . . АЧХ, ФЧХ связаны с импульсной характеристикой преобразованием Фурье. Эта связь взаимно однозначна. Для получения АЧХ из импульсной характеристики нужно взять прямое преобразование Фурье, а чтобы из АЧХ получить импульсную характеристику нужно взять обратное преобразование Фурье. В чём особенности частотных характеристик цифровых фильтров и чем они обусловлены? Информативной характеристикой является АЧХ. АЧХ определяется весовыми коэффициентами и порядком фильтра. Порядок фильтра равен числу элементов задержки. Коэффициенты фильтра и АЧХ связаны преобразованием Фурье. Рекурсивные фильтры обычно имеют меньший порядок в отличаи от нерекурсивного. Рекурсивный и нерекурсивный линейные фильтры позволяют реализовать фильтры с следующими типами избирательности: фильтр нижних частот, фильтр верхних частот, полосовой фильтр, режекторный фильтр, многополосный фильтр. Рис 1. Примеры АЧХ фильтров 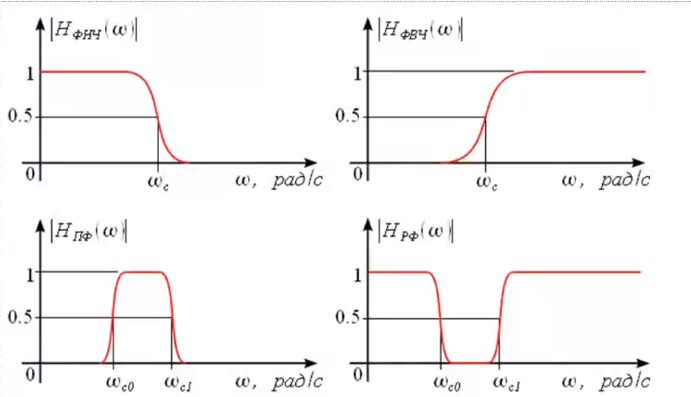  АЧХ зависит как от коэффициентов фильтра, так и от его порядка. Характеристики фильтра можно разделить на временные и частотные. Частотные характеристики — это характеристики у которых какая-то из осей (обычно ось абсцисс) является частотой или какой-то характеристикой, связанной с частотой (нормированной частотой, соотношение частот). Временные характеристики — это реакция фильтра на какой-то сигнал строго определенной формы. Если нерекурсивный фильтр имеет одинаковы значения коэффициентов равные 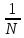 , то это усредняющий фильтр (сглаживающий). АЧХ такого фильтра всегда соответствует АЧХ фильтра нижних частот. С увеличением порядка данный фильтр становится более узкополосным и растёт затухание. , то это усредняющий фильтр (сглаживающий). АЧХ такого фильтра всегда соответствует АЧХ фильтра нижних частот. С увеличением порядка данный фильтр становится более узкополосным и растёт затухание. 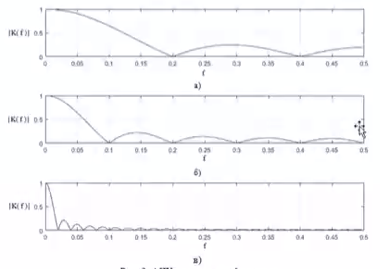 Как отображаются нули и полюсы цифрового фильтра на комплексной Z-плоскости и какую информацию о фильтре можно получить по картине его нулей и полюсов? Нулю и полюсы ПФ. У дробной функции есть понятие нулей и полюсов. Нули — это значения переменных, при которых функция равна нулю (корни числителя). Полюсы — это корни при которых знаменатель равен нулю и, следовательно, вся дробь будет равна бесконечности. Полюсы — это ключевая характеристика устойчивости фильтра. По расположению на комплексной плоскости можно судить о том является фильтр устойчивым или нет. 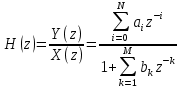
Расположение нулей на устойчивость фильтра не влияет. Матлаб всегда синтезирует коэффициенты фильтра так чтобы фильтр получился устойчивым. Но при переносе полученных коэффициентов на с программу могут возникнуть проблемы. Из-за переполнения разрядов часть числа отбросится и это приведёт к тому, что фильтр может стать неустойчивым. Какие возможны формы реализации рекурсивных фильтров и как они описываются математически? АЧХ строится от нуля до половины частоты дискретизации. В соответствие с теоремой Котельникова. При увеличении частоты дискретизации все характеристики фильтра растянуться от масштабируются. Что понимается под синтезом цифрового фильтра? Коэффициенты фильтра синтезируются на основании АЧХ. Эти коэффициенты и АЧХ связанны преобразованием Фурье. Под синтезом цифрового фильтра понимается процесс вычисления его весовых коэффициентов по заданной АЧХ. Что понимается под адаптивным цифровым фильтром? Какие задачи он решает? Параметры адоптивного фильтра меняются в соответствии алгоритму. В зависимости от входного сигнала. Его параметры являются переменными. В процессе своего функционирования адоптивный фильтр меняет свою АЧХ. Существует жёсткая связь между АЧХ фильтра и его коэффициентами. Для получения АЧХ из импульсной характеристики нужно взять прямое преобразование Фурье, а чтобы из АЧХ получить импульсную характеристику нужно взять обратное преобразование Фурье.
|