Ответы на экзамен. Ответы на экзаменэ. Экзаменационные вопросы по дисциплине Цифровая обработка сигналов
 Скачать 2.67 Mb. Скачать 2.67 Mb.
|
|
Задачи, решаемые адоптивными фильтрами различны. Задача активного шумоподавления, сжатие речи, голосовой датчик в сотовых телефонах. При изменении параметров сигнала так же меняется и адоптивный фильтра поэтому АЧХ можно использовать для характеристики определённого сигнала. В сотовой связи по линии передачи не передаются отчёты сигнала, а передаются некие заархивированные параметры коэффициенты адоптивного фильтра. Звуковая дорожка разделяется на малые промежутки, к примеру по 120 ms. Каждый промежуток представляется в виде АЧХ некоего адоптивного фильтра. Сигнал на каждом таком участке подаётся на вход адоптивного фильтра и коэффициенты этого адоптивного фильтра настраиваются так чтобы его выходной сигнал был максимально похож на сигнал на заданном промежутке (120 ms). Будет наеден оптимальный набор коэффициентов адоптивного фильтра тоесть тот набор при котором выходной сигнал адоптивного фильтра максимально похож на сигнал на входе. И получается, что сигнал на заданном промежутке характеризуется набором коэффициентов адоптивного фильтра. Коэффициентов фильтра гораздо меньше, чем отчётов сигнала. Сжатие речи осуществляется с помощью адоптивных фильтров. Алгоритмы сжатия речи используют разные параметры сигнала. Анализируется дисперсия, среднеквадратическое отклонение по ним оценивается говорит абонент или нет. Так же выполняется анализ сигнала на разных участках. Сначала сигнал анализируется на коротких участках, а затем выполняется анализ на большом промежутке времени. Речевой кодер выполняет дискретизацию сигнала. Речевой кодер — это вычислитель, выполняющий сжатие речи. Когда абонент молчит нет никакого смысла передавать сигнал, который не несёт никакой информации и засорять канал передачи. Задачу определения молчит пользователь или нет выполняет датчик активности голоса. На определённой порции отсчётов, которая передаётся в виде коэффициентов фильтра (к примеру, 160) анализируется по дисперсии. Что такое сигнал ошибки адаптивного цифрового фильтра? Что такое рабочая функция адаптивного фильтра? Адоптивный фильтр должен иметь алгоритм изменения весовых коэффициентов фильтра (алгоритм адаптации). В структурную схему адоптивного фильтра обязательно входит вычислитель (блок адаптации) весовых коэффициентов. Вычислитель основан на базе микропроцессоров, флисах, пк, специальных ядер предназначенных для обработки сигналов. Подбор коэффициентов должен происходить по определённым критериям оптимальности. Функционирование АФ привязано к тому, что он использует некие критерии оптимальности и способен к обучению. Чтобы перестраивать весовые коэффициенты нужно знать: как изменяется входной сигнал, для правильной настройки весовых коэффициентов должен быть известен эталонный сигнал. Обучение происходит путём того, что на вход фильтра подаются отчёты сигнала, но при этом цифровой фильтр знает какую требуемую реакцию он должен выработать. Цифровой фильтр обучается на выборке сигналов. Выход адоптивного фильтра может сравниваться с сигналом, который использовался в качестве эталонного сигнала (чистый сигнал без шума). Критерии оптимальности зависят от поставленной задачи. Функционирование адоптивного цифрового фильтра должно улучшаться со временем. Адоптивный фильтр должно уметь функционировать после обучения и без эталонного сигнал. Адоптивные фильтры применяются при сжатии речи в системах сотовой связи в качестве «предсказателей». Реализация адоптивного цифрового фильтра в основном программная. При использовании обычного цифрового фильтра необходимо знать какие полосы частот соответствуют полезному сигналу, какие полосы частот соответствуют полезному сигналу. Задача сводится к следующему: полезный сигнал сосредоточен в некой узкой полосе, а шум занимает широкую полосу в зависимости от того в какой области частот располагается спектр сигнала используются разные фильтры (ФВЧ, ФНЧ, полосовой, режекторный и др). Неизбежно то что в полосу пропускания фильтра будет попадать и часть шума. Полоса частот полезного сигнала может изменится (расширятся или сужаться) или может происходить с течением времени перемещение полосы полезного сигнала по оси частот. В таком случае обычный цифровой фильтр уже не подойдёт. Это связано с тем, что если фильтр сделать слишком широким, то в полосу пропускания будет пролазить большая доля шумов. Если фильтр сделать узким, то в этом случае сигнал, изменивший свои характеристики, может этим фильтром подвалятся. Поэтому адоптивный фильтр должен отслеживать меняющиеся характеристики сигнала и если характеристики сигнала каким, то образом поменялись (ширина спектра, центральная частота полосы этого спектра), то адоптивный алгоритм (алгоритм адаптации) адоптивного фильтра должен отслеживать эти изменения и соответствующе на них реагировать. Адоптивные алгоритмы это отслеживают по косвенным признакам. Алгоритм адаптации должен применять такие правила, при которых признаки изменения сигнала давали бы команду правильно перестроить коэффициенты цифрового фильтра. На этапе обучения необходимо иметь эталонный (обучающий сигнал). У обучающегося фильтра есть рассогласование (сигнал ошибки) разность между эталонным сигналом и выходным сигналом.
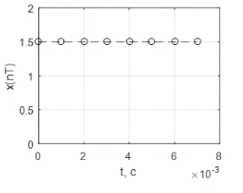
СКО критерий который используется для случая, когда необходима чтобы форма сигнала была сохранена. Среднеквадратическая ошибка представляет собой поверхность, которая зависит от весовых коэффициентов. 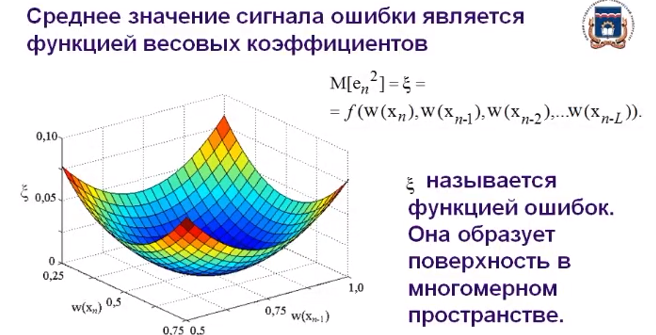 Задача адоптивного цифрового фильтра спустится в самую нижнюю точку данной поверхности. У поверхности может быть более одной точки минимума. Но один или несколько минимумом в любом случае имеется. Приведите структурную схему адаптивного нерекурсивного цифрового фильтра. 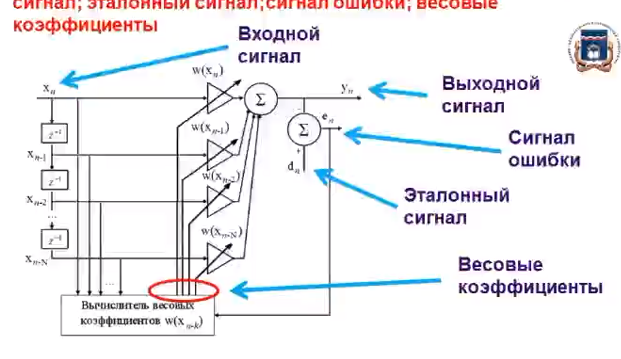 17. Какие задачи решаются с помощью дискретного преобразования Фурье? Для чего предназначено прямое дискретное преобразование Фурье? Какими свойствами должна обладать функция, используемая в качестве исходных данных для прямого дискретного преобразования Фурье? ДПФ это алгоритм, который позволяет получать амплитудный спектр сигнала из временной формы сигнала. ДПФ позволяет из временной формы сигнала получить частотную форму. Обратное преобразование Фурье позволяет получить из частотной формы сигнала временную. ДПФ есть ничто иное как разложение дискретного сигнала на гармонические составляющие. Произвольный сигнал представляется в виде суммы гармоник (синусоид, косинусоид). В ряд Фурье можно раскладывать любые сигналы, периодические и непериодические. Гармонический сигнал раскладывается сам в себя. Прямое преобразование Фурье: 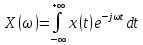 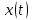 – аналоговый сигнал, t – время, – аналоговый сигнал, t – время, 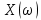 – спектральная плотность сигнала (Фурье-образ), – спектральная плотность сигнала (Фурье-образ), 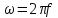 – циклическая частота сигнала, f– частота в герцах,j – мнимая единица. – циклическая частота сигнала, f– частота в герцах,j – мнимая единица.Прямое преобразование Фурье исходными данными использует временное представление сигнала, а результатом преобразования является спектральное представление сигнала. Обратное преобразование Фурье использует представление сигнала в частотной области, а результатом преобразования является временная форма сигнала. Дискретное преобразование Фурье: 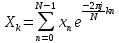 ПФ применяется к аналоговым сигналам а ДПФ применяется к дискретным сигналам. Результат прямого преобразования Фурье — это всегда функция комплексная. Ограничений к функции почти никаких нет. Функция должна иметь конечную длину (должна обладать конечной энергией). Свойство ДПФ. 18. В какой форме представляется результат прямого дискретного преобразования Фурье? Какую информацию содержит в себе результат прямого дискретного преобразования Фурье? Как связан результат прямого дискретного преобразования Фурье со спектром дискретного сигнала? Прямое преобразование Фурье исходными данными использует временное представление сигнала, а результатом преобразования является спектральное представление сигнала. Результат прямого преобразования Фурье — это всегда функция комплексная. Количество комплексных числе полученных в результате прямого преобразования Фурье, всегда равно количеству отсчётов сигнала во временной форме. ДПФ есть ничто иное как разложение дискретного сигнала на гармонические составляющие. Произвольный сигнал представляется в виде суммы гармоник (синусоид, косинусоид). В ряд Фурье можно раскладывать любые сигналы, периодические и непериодические. Гармонический сигнал раскладывается сам в себя. Спектр — это разложение на что-то. Разложение сигнала на частоты, содержащиеся в нём. По оси абсцисс откладывается частота в диапазоне от 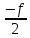 до до 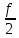 , если это математический спектр и от 0 до , если это математический спектр и от 0 до 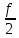 , если это физический спектр. В цифровой обработке сигналов информативным является физический спектр. , если это физический спектр. В цифровой обработке сигналов информативным является физический спектр. Результат ДПФ обычно содержит отрицательные частоты. Если имеются 100 отсчётов сигнала, то получится 100 отсчётов амплитудного спектра и обязательно 50 из этих будет отдано на представление отрицательных частот. После преобразования Фурье, по сути, получается 200 чисел (мнимая и действительная части). На каждый отчёт сигнала приходится одно комплексное число. У этих комплексных чисел берётся модуль и аргумент. Модуль откладывается по оси ординат и получается амплитудный спектр. Если по оси ординат отложить аргумент, то получится фазовый спектр. Спектр можно представить в виде математического спектра либо в виде физического спектра. При ДПФ получается математический спектр. Математический амплитудный спектр гармонического сигнала с частотой 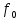 и амплитудой и амплитудой 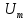 является комбинацией из двух дельта-функций, расположенных в точках является комбинацией из двух дельта-функций, расположенных в точках 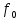 и и 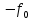 и с коэффициентом и с коэффициентом 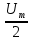 . Если убрать отрицательные частоты, то из математического спектра можно получить физический. . Если убрать отрицательные частоты, то из математического спектра можно получить физический.Дискретное преобразование Фурье выполняется в несколько этапов. Первичным результатом является результат с порядковым номером отсчёта. Затем выполняется переход к частоте. Для сигнала, который представляет собой прямую постоянную во времени линию, то на спектре будет видно, что максимум находится на нулевой частоте. Сигнал с амплитудной модуляцией. Синусоида модулирована по амплитуде каким-то импульсом. Спектр будет смещён на частоту модулированной синусоиды. Прямоугольный импульс имеет самый широкий спектр. Самый узкий спектр имеет треугольный сигнал. Спектр последовательности дискретный, а спектр одиночного импульса непрерывной. Непрерывный значит, что точки спектрального отчёта нужно соединить кривое. Дискретный спектр представляет собой просто ряд спектральных отчётов. Для сигнала, который представляет собой прямую постоянную во времени линию, то на спектре будет видно, что максимум находится на нулевой частоте.
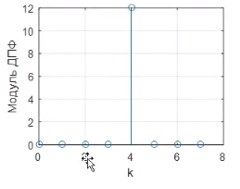
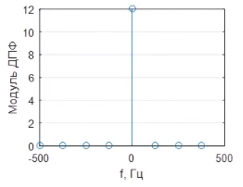
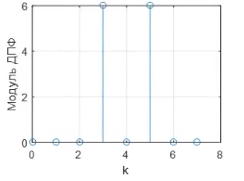
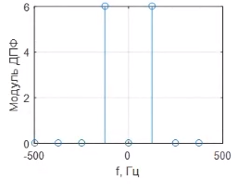
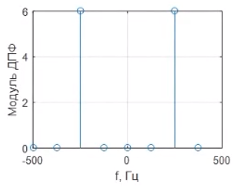
Гармонический сигнал. С частотой 125 Гц.
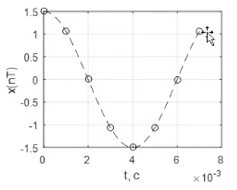
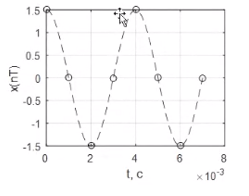
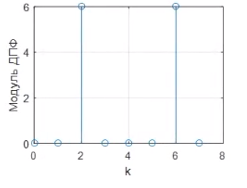
Гармонический сигнал. С частотой 250 Гц.
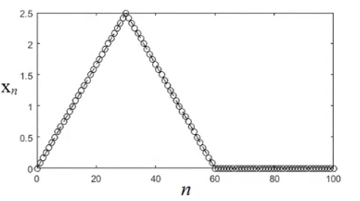
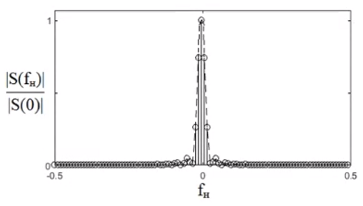
Диапазон берётся  в соответствии с теоремой Котельникова. в соответствии с теоремой Котельникова. Треугольный видеоимпульс.
  Аргументом комплексного числа называется угол, который образует вектор комплексного числа с положительным направлением оси абсцисс. Из-за этого график математического спектра симметричен. Фазовый спектр наиболее важен не для сигнала, а для устройства. ФЧХ показывает, как будет задерживать фильтр те или иные частоты, она показывает какой фазовый сдвиг будет вносить фильтр для конкретной частоты. Фазовый спектр сигнала показывает из гармоник с какими начальными фазами состоит сигнал. 19. Перечислите основные свойства дискретного преобразования Фурье. Поясните их смысл. ДПФ линейно. Преобразование Фурье линейной комбинации функций будет такой же линейной комбинацией результатов преобразования Фурье этих функций по отдельности. Данное свойство позволяет сводить сложные функции и их спектры к более простым. К примеру, есть сигнал с определённым спектром и есть шум со своим спектром, то сумма сигнал шум будет иметь спектр, который будто представлять собой сумму двух спектров. Примером так же является математический амплитудный спектр, рассмотренный выше. Если взять функцию, состоящую из суммы множества гармонических сигналов с разными частотами, то согласно свойству линейности амплитудный спектр этой функции будет состоять из соответствующего набора дельта функций. Задержка. Амплитудный спектр не зависит от сдвига сигнала по времени. Если сдвинуть функцию влево или вправо по оси t, то поменяется лишь её фазовый спектр. Растяжение сжатие. Возможность растяжения сжатия исходной функции по оси времени. Растяжение исходной функции по оси t пропорционально сжимает её амплитудный спектр по оси частот f. И наоборот сжатие исходной функции по оси t пропорционально растягивает её амплитудный спектр по оси частот f. В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности. Чем более длительным является импульс, тем уже у него спектр. Чем более узкий импульс, тем более широкий у него спектр. Чем меньшую длительность имеет импульс, тем из синусоид с большими частотами будет этот импульс состоять. Свёртка функций. Возможность свести свёртку функций к поточечному перемножению их Фурье-образов. Данное свойство служит основой для алгоритмов линейной цифровой фильтрации. Любой цифровой фильтр работает во временной области. Коэффициенты фильтра перемножаются с отчётами сигнала и таким образом получается выходной сигнал. Но в таком случае происходит неизбежное преобразование в частотной области так как временная и частотная область связаны друг с другом. По сути, перемножается Фурье-образ сигнала и АЧХ фильтра. К примеру, если дельта функции попадает в полосу пропускания, то она перемножается с единицей, а если в область задерживания, то к числу близкому к нулю. Поточечное перемножение. Возможность свести поточечное перемножение функций к свёртке из Фурье-образов. Данное свойство используется для проектирования цифровых фильтров. Задаётся АЧХ и по нему создаются коэффициенты фильтра. Симметрия. Симметрия амплитудного спектра вещественного сигнала. На практике большинство сигналов описываются действительными функциями. Амплитудный спектр действительнозначной функции является чётной функцией, а фазовый спектр (если его перевести к диапазону от 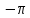 до до 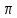 ) – нечётный. По этой причине на графиках спектров часто не изображают отрицательную часть спектра. Тоесть изображают только в виде физического спектра. Для действительнозначимых сигналов часть спектра, соответствующая отрицательным частотам, не даёт никакой новой информации. ) – нечётный. По этой причине на графиках спектров часто не изображают отрицательную часть спектра. Тоесть изображают только в виде физического спектра. Для действительнозначимых сигналов часть спектра, соответствующая отрицательным частотам, не даёт никакой новой информации.Применение для сигналов, имеющих конечную энергию. Применение ПФ к сигналам, имеющим конечную энергию. Преобразование Фурье осмысленно только для сигналов конечной продолжительности. Спектр таких сигналов должен быть отличным от нуля только на некотором конечном временном отрезке. Последовательность, к которой применяется ПФ должна быть конечной. Любой дискретный сигнал является конечным. 20. Что такое быстрое преобразование Фурье? При каких условиях достигается наибольшее ускорение вычислений при выполнении алгоритма быстрого преобразования Фурье? |