Пропорциональное звено - это звено, для которого в любой момент времени выходная величина пропорциональна входной. Его уравнение: y(t) = k u(t). u(t). Передаточная функция: W(p) = k. Переходная характеристика: h(t) = k 1(t). 1(t). Любое реальное звено обладает инерционностью, но с определенной точностью. Некоторые реальные звенья могут рассматриваться как безынерционные, например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель и т.п. В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе и сохраняет это значение. При k = 1 звено никак себя не проявляет, а при k = - 1 - инвертирует входной сигнал. Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее jω вместо p, получим АФЧХ W(jω). Затем надо выразить из нее вещественную ЧХ P(ω) и мнимую ЧХ Q(ω). После этого преобразуют АФЧХ в показательную форму и получают АЧХ A(ω) и ФЧХ φ(ω), а затем определяют выражение ЛАЧХ L(ω) = 20lgA(ω) (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс). АФЧХ: W(jω) = k. ВЧХ: P(ω) = k. МЧХ: Q(ω) = 0. АЧХ: A(ω) = k. ФЧХ: φ(ω) = 0. ЛАЧХ: L(ω) = 20lgk. Типовые динамические звенья первого порядка подразделяются на статические, астатические, дифференцирующие и звено чистого запаздывания. К статическим относятся такие звенья, которые при ступенчатом входном воздействии переходят из начального положения равновесия в новое. Это звено называют также усилительным и безынерционным. Звено описывается алгебраическим уравнением y = к × x , где k – коэффициент передачи (усиления), имеющий размерность единицы выходной величины y, деленную на единицу входной величины x. Передаточная функция пропорционального звена равна его коэффициенту передачи – W(p) = k. Усилительное звено не трансформирует форму входного сигнала, а изменяет только его масштаб в k раз. Примерами пропорциональных звеньев могут служить: а) рычаг, если входная величина х – усилие на одном конце рычага, а выходная величина у – усилие на другом его конце; б) зубчатая передача, если х = jвх – угол поворота малой шестерни, а у = jвых – угол поворота большой шестерни; в) теплоотдача конвекцией от движущегося газа к стенке, если х –разность температур газа и стенки D t = tГ – tСT, а у – количество отдаваемого тепла Q; г) потенциометрический датчик измерительного прибора, если х – перемещение движка l, a у – снимаемое с датчика напряжение Uвых. Звено апериодическое первого порядка (инерционное).
Динамика этого звена описывается дифференциальным уравнением
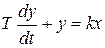 , ,
где k – коэффициент передачи; Т – постоянная времени, с.
Передаточная функция звена
W(p) = k / (Tp+1).
Переходная характеристика звена h(t) = k (1 – e – t / T).
Таким образом, звено накапливает энергию или вещество и, благодаря этому, Y принимает свое значение через время.
Следовательно, постоянная времени – это время, за которое выходная величина достигла бы своего установившегося значения, если бы изменялась с постоянной начальной скоростью. Чем больше Т, тем длительнее переходный процесс. Практически переходный процесс считается закончившимся через время t » 3 Т.
Примерами апериодических звеньев могут служить:
а) электропривод постоянного тока, если входная величина х подводимое напряжение и, а выходная величина у – скорость вращения n;
б) промежуточный ковш МНЛЗ, если х = Gпр – Gот – баланс поступления и расхода жидкого металла, а у – уровень металла Н;
в) нагрев тела, помещенного в среду с температурой tc (теплоотдача оценивается по закону Ньютона q = a (tc – tм), где q – плотность теплового потока на нагреваемое тело; a – коэффициент теплоотдачи), если tc – входная величина, а средняя температура тела tм – выходная величина;
г) электрическая RC-цепочка, если Uвх = х, а Uвых = у.
|
 Скачать 317.1 Kb.
Скачать 317.1 Kb.