Главная страница
Навигация по странице:

  • Частотная передаточная функция

  • оси абсцисс.

    		•

    ответы на вопросы. тау. Экзаменационные вопросы по предмету тау


    Скачать 317.1 Kb.
    НазваниеЭкзаменационные вопросы по предмету тау
    Анкорответы на вопросы
    Дата12.01.2023
    Размер317.1 Kb.
    Формат файлаdocx
    Имя файлатау.docx
    ТипЭкзаменационные вопросы
    #883065
    страница2 из 4
    1   2   3   4
    электронные усилители – устройства, позволяющие увеличить мощность электрического сигнала без изменения его формы и частотного спектра. Увеличение мощности сигнала происходит за счет энергии источника питания.

    Ко входу усилителя подключается источник сигнала  к выходу – нагрузка .

    Операционный усилитель (ОУ) является усилителем постоянного тока (УПТ) с очень большим коэффициентом усиления. Словосочетание «усилитель постоянного тока» не означает, что операционный усилитель может усиливать только постоянный ток. Имеется в виду, начиная с частоты в ноль Герц, а это и есть постоянный ток.

    Термин «операционный» укрепился давно, так как первые образцы ОУ использовались для различных математических операций типа интегрирования, дифференцирования, суммирования и тд. Коэффициент усиления ОУ зависит от его типа, назначения, структуры и может превышать 1 млн.

    Принцип работы ОУ очень прост. Он сравнивает два напряжения и на выходе уже выдает отрицательный, либо положительный потенциал питания. Все зависит от того, на каком входе потенциал больше. Если потенциал на неинвертирующем входе U1 больше, чем на инвертирующем U2, то на выходе будет +Uпит, если же на инвертирующем входе U2 потенциал будет больше, чем на НЕинвертирующем U1, то на выходе будет -Uпит.

    1. Измерительные устройства и их характеристики.

    Измерительное устройство служит для получения информации о состоянии объекта и по обратной связи эта информация в виде сигналов подается в регулятор, вместе с полезной информацией в регулятор также поступают помехи. В общем случае комплекс измерительных средств системы сам по себе является динамической системой и описывается дифференциальными уравнениями.

    Входами в такой системе являются переменные состояния объекта и помехи, а выходами измеряемые переменные. В тех случаях, когда динамикой измерительных устройств пренебрегать нельзя, дифференциальные уравнения измерителей относят к уравнениям объекта, а для описания выходных переменных измерителей используют алгебраические уравнения:   σ(t) – измеряемая величина, v(t) – помеха.

    Чаще всего в системах с обратной связью на вход регулятора подаются сигналы, отражающие разность между заданным и истинным состоянием объекта.

    Если в системе происходит измерение нескольких параметров:  , причем каждое уравнение будет описывать отдельный параметр. Для того чтобы описать все контролируемые параметры используется понятие матрицы.  , где С[i]- матрица контролируемых параметров, x(t) – помехи,   - все контролируемые параметры.

    При проектировании систем измерительное устройство выбирают так, чтобы диапазон измерения приходился на линейный участок статической характеристики, а возможные нелинейные эффекты были незначительны. Исполнительные устройства служат для передачи и преобразования управляющего воздействия на объект управления. Они бывают разного рода. И исполнительные устройства и устройства измерения относятся к неизменяемой части системы, поэтому при составлении модели системы их собственную динамику относят к объекту управления.

    Основные датчики в автоматизированном оборудовании можно разделить на следующие группы:

    1) датчики положения: а) датчики линейного перемещения, б) датчики фиксированных положений;

    2) датчики скорости;

    3) датчики температуры (окружающей среды, рабочей жидкости и др.);

    4) датчики усилия (например, усилия резания по цифровому датчику давления).

    Сельсином называется информационная электрическая машина переменного тока, вырабатывающая напряжения, амплитуды и фазы которых определяются угловым положением ротора. Сельсины позволяют осуществить без общего механического вала согласованное вращение или поворот механизмов. Известны два режима работы сельсинов: индикаторный и трансформаторный. При работе сельсинов в индикаторном режиме происходит передача на расстояние угла поворота механической системы. При работе сельсинов в трансформаторном режиме передается сигнал, воздействующий на исполнительный механизм таким образом, чтобы заставить его отработать заданный поворот.

    Синусно-косинусный вращающийся трансформатор, резольвер (anglecomponent solver) - синусно-косинусный датчик угла, представляющий трансформатор, состоящий из ротора и статора, несущих по паре взаимноперпендикулярных обмоток.

    При повороте ротора в зависимости от режима Датчики автоматизированных электроприводов работы изменяются амплитуды (пропорционально синусу и косинусу угла поворота) или фаза напряжения вторичных обмоток.

    Различают: 1) синусно-косинусные поворотные трансформаторы (СКПТ), которые выдают два напряжения, изменяющиеся по гармоническому закону Us= Umsina и Uc = Umcosa;

    2) линейные поворотные трансформаторы (ЛПТ), выходное напряжение которых изменяется по закону U = ka.

    Поворотным, или вращающимся, трансформатором называется информационная электрическая машина, амплитуда выходного напряжения которой является функцией входного напряжения и углового положения ротора.

    Поворотные трансформаторы конструктивно сходны с асинхронными машинами с фазным ротором и контактными кольцами. К ним обычно подводится питание со стороны статора от источника переменного напряжения. На обмотке ротора (на выходе) получают напряжение, представляющее собой определенную функцию угла поворота ротора α. Обычно требуется, чтобы это напряжение было пропорционально sinα, cosα. В соответствии с этим, различают синусные, косинусные и синус - косинусные трансформаторы.

    Резольвер работает по принципу вращающегося трансформатора. У вращающегося трансформатора ротор состоит из катушки (обмотки), которая вместе с обмоткой статора образует трансформатор. Принципиально резольвер устроен точно так же с той лишь разницей, что статор выполнен не из одной, а из двух расположенных под углом 90 градусов друг к другу обмоток. Резольвер служит для определения абсолютного положения вала двигателя внутри одного оборота. Кроме того, по сигналу резольвера определяется значение скорости и моделируется инкрементный датчик для регулирования положения.

    Энкодеры – преобразователи информации об абсолютном или относительном угловом положении вала в кодовый цифровой сигнал.

    Абсолютный энкодер, как правило, отличается наличием уникальной комбинации меток в виде линий или секций переменной угловой ширины для каждого углового положения, а инкрементальный энкодер использует диск, на котором равномерно нанесены однотипные метки (за исключением, индексной), поскольку основная задача инкрементального устройства — детектирование пошагового перемещения с опорой на нулевую (индексную) метку при включении питания. Энкодеры с большим интервалом между масштабными штрихами (с меньшим количеством штрихов) обеспечивают более высокую частоту выдачи данных, в то время как энкодеры с меньшим интервалом между штрихами (большим количеством штрихов), как правило, имеют более низкие ошибки интерполяции.

    Строго говоря, угловыми энкодерами называются преобразователи угловых перемещений, имеющие 10 000 и более масштабных штрихов на оборот, точность которых не хуже 5 угловых секунд, а под «круговыми датчиками» подразумеваются энкодеры, которые не удовлетворяют этим критериям. Вместе с тем, зачастую угловым энкодером называют любой преобразователь угловых перемещений.

    1. Исполнительные элементы. Примеры исполнительных элементов (сервоприводы).

    Исполнительные устройства — электромагниты с втяжным и поворотным якорями, электромагнитные муфты, а также электродвигатели, относящиеся к электромеханическим исполнительным элементам автоматических устройств.

    Наиболее широко в качестве электромеханических исполнительных элементов применяют электродвигатели постоянного и переменного тока.

    Исполнительные элементы (ИЭ) систем автоматики предназначены для создания управляющего воздействия на регулирующий орган (РО) объекта управления (ОУ). При этом изменяется положение или состояние РО, что приводит в конечном итоге к изменению положения или состояния ОУ в соответствии с алгоритмом управления.

    Еще одним вариантом ИЭ является следящий привод, который воспроизводит на выходе заданное на входе перемещение, но с большим механическим усилием, т.е. момент или сила на выходе его существенно больше, чем на входе. Следящий привод широко применяется в автоматических манипуляторах (роботах), станках с числовым программным управлением (ЧПУ), для управления прокатными станами, антеннами радиолокаторов, в космической и ракетной технике и т. д.

    Исполнительный элемент {исполнительное устройство) — функциональный элемент системы автоматического управления, осуществляющий воздействие на объект управления путем изменения потока энергии и потока материалов, поступающих на объект. Исполнительные элементы в основном бывают двух типов:

    с механическим двигателем (в частности, сервомотор, серводвигатель или сервопривод), в этом случае исполнительный элемент производит механическое перемещение регулирующего органа;

    с электрическим выходом, в этом случае воздействие, непосредственно прикладываемое к объекту регулирования, имеет электрическую природу.

    Например, в регуляторе напряжения генератора постоянного тока регулирующим воздействием является напряжение возбуждения, получаемое от усилителя.

    В зависимости от характера объекта и вида вспомогательной энергии, применяемой в системе автоматического управления, роль исполнительных элементов выполняют самые разные конструктивные элементы: электронные, электромашинные, магнитные или полупроводниковые усилители, реле, пневматические или гидравлические сервомоторы и др.

    Динамические характеристики исполнительных элементов с механическим выходом отличаются значительно большей инерционностью, чем элементы с электрическим выходом. Часто исполнительные элементы второго типа служат приводом исполнительных элементов первого типа.

    Сервоэлектродвигатели, применяемые в качестве исполнительных элементов с механическим выходом, отличаются специальным исполнением, обеспечивающим пониженную инерционность (удлиненным ротором малого диаметра, полым ротором). Значительно меньшую инерционность при той же мощности имеют гидравлические и пневматические серводвигатели.

    Требования к исполнительным элементам определяются характеристиками объекта регулирования и требуемым качеством процесса регулирования.

    Исполнительный механизм (сервопривод) — исполнительный элемент с механическим выходом. Исполнительные механизмы классифицируются по назначению и типу управляемых элементов, виду осуществляемых перемещений, роду применяемой энергии.

    Исполнительные механизмы предназначаются для привода:

    элементов, регулирующих потоки энергии, жидкости, газа, сыпучих и перемещаемых твердых тел (реостатов, клапанов, задвижек и заслонок, направляющих аппаратов турбин и насосов, шлагбаумов и других устройств);

    элементов следящих систем (копировальных станков, манипуляторов, автокомпенсационных, регулирующих и других устройств);

    рулевых устройств транспортных объектов;

    особых элементов систем управления (противовесов в грузоподъемных сооружениях, зажимных автоматических устройств и т.п.).

    Управление электрическим исполнительным механизмом с помощью соответствующих обратных связей можно построить так, чтобы перемещение регулирующего органа или скорость его движения изменялись пропорционально сигналу управления.

    Конструктивно электродвигательные исполнительные механизмы выполняются, как правило, с вращательным движением выходного вала и реже с поступательным перемещением выходного штока. В системах общепромышленной автоматики для привода заслонок, кранов, шиберов и других устройств наиболее часто применяются однооборотные электрические исполнительные механизмы, в которых поворот выходного вала составляет 120... 170°. С помощью многооборотных электрических исполнительных механизмов обычно перемещаются такие регулирующие органы, как запорные вентили и задвижки.

    1. Корректирующие устройства (основные характеристики, примеры реализации)

    Смысл введения в автоматическую систему корректирующих устройств можно пояснить, рассмотрев их влияние на изменение частотных характеристик автоматической системы. Неустойчивая автоматическая система может быть приведена к устойчивой путем коррекции АФЧХ с обеспечением достаточного запаса устойчивости.

    Отметим основные особенности постановки и решения задачи синтеза корректирующих устройств:
         1. Обычно автоматическая система содержит объект регулирования и звенья с трудно изменяемыми параметрами и характеристиками, а также она содержит звенья с легко изменяемыми параметрами и характеристиками, которые служат для придания автоматической системе требуемых динамических свойств. Эти функции возлагаются на корректирующие устройства автоматических систем;
          2. При синтезе корректирующих устройств важно знать оптимальные динамические характеристики автоматической системы, к реализации которых следует стремиться. Условия качества работы задаются лишь на верхние допустимые границы отдельных показателей качества. Они ограничивают лишь область допустимых значений, но не определяют однозначно характер переходного процесса. Поэтому задачей синтеза корректирующих устройств является получение требуемого качества работы, определяемого областью допустимых значений регулируемой величины;
          3. Решение задачи синтеза корректирующих устройств не является однозначным. Одни и те же требования можно удовлетворить при помощи различных корректирующих устройств. На практике в таких случаях выбирают такое корректирующее устройство, которое технически наиболее просто осуществимо;
          4. Вследствие сложности многих современных автоматических систем, являющихся динамическими системами со многими степенями свободы, содержащими кроме постоянных и переменные, а иногда и распределенные параметры. Во многих случаях нельзя получить точных результатов расчетным путем, поэтому теоретический анализ и расчет обычно имеют целью лишь облегчить выбор рациональной структурной схемы автоматической системы.

    Синтез корректирующих устройств автоматических систем состоит из следующих этапов:
          1. Анализа свойств объекта регулирования и определения его статических и динамических характеристик;
          2. Формулировки и обоснования критерия оптимальности, условий качества регулирования и других требований, которым должна удовлетворять автоматическая система;
          3. Выбора структурной схемы автоматической системы и технических средств ее реализации;
          4. Синтеза оптимальных динамических характеристик автоматической системы;
          5. Аппроксимации оптимального режима, т. е. выбора желаемых характеристик, отвечающих качеству регулирования и простотой технической реализации;
          6. Определения желаемых динамических характеристик корректирующих устройств, обеспечивающих требуемые динамические свойства автоматической системы в целом;
          7. Выбора схемы и способа технической реализации корректирующих устройств;
          8. Анализа полученной схемы автоматической системы, цель которого состоит в проверке расчетным или экспериментальным путем соответствия полученного результата требованиям технического задания.

    Существует три основных типа корректирующих устройств - последовательное, параллельное и обратная связь. Использование того или иного типа корректирующих устройств определяется удобством их технической реализации. 

    В некоторых учебниках и справочниках приводятся таблицы, содержащие схемы сотен корректирующих звеньев различного типа на все случаи жизни. В линейных автоматических системах динамические свойства их при введении корректирующих устройств различного типа могут быть сделаны одинаковыми, и для корректирующего устройства одного типа можно подобрать эквивалентное корректирующее устройство другого типа. Эквивалентность обозначает, что присоединение к системе автоматического регулирования одного или другого корректирующего устройства образует полностью подобные в динамическом отношении автоматические системы.

    К основным корректирующим устройствам относятся:
          1. Пассивные корректирующие устройства - это такие устройства, которые не требуют подвода энергии из вне автоматической системы;
          2. Активные корректирующие устройства - это такие устройства, для нормального функционирования которых требуется подвод энергии от постороннего источника.

    1. Преобразующие устройства (основные характеристики, примеры - магнитный, электромашинный усилитель )

    Преобразующие устройства служат для преобразования управляющих и информационных сигналов в устройствах автоматики к виду, удобному для их последующей обработки или фиксации. Преобразующие устройства должны иметь малую инерционность и хорошую согласованность с другими узлами автоматики, достаточно высокое быстродействие.

    Магнитным усилителем называется устройство, использующее дроссель насыщения (в простейшем виде сердечник из ферромагнитного материала с двумя обмотками – переменного и постоянного тока) в сочетании с другими элементами для усиления или преобразования различных электрических сигналов.

    Действие магнитных усилителей основано на свойстве дросселя насыщения изменять свою индуктивность под влиянием подмагничевающего поля, что в свою очередь обуславливается нелинейным характером кривой намагничивания ферромагнитных материалов.

    Достоинствами магнитных усилителей являются большой срок службы, надежность в эксплуатации, большая ударная и вибрационная стойкость, простота суммирования большого числа сигналов.

    Применяемые в настоящее время схемы магнитных усилителей очень многообразны. По виду нагрузочной характеристики магнитные усилители делятся на реверсивные и нереверсивные, по способу осуществления обратной связи – на усилители с внешней и внутренней обратной связью. Различаются усилители однополупериодные, с выходом на постоянном токе и с выходом на переменном токе, однофазные, трехфазные и многофазные.

    Электромашинные усилители (ЭМУ) применяют на судах в схемах автоматического регулирования, а также в качестве возбудителей генераторов и двигателей.

    Простейшим ЭМУ является генератор постоянного тока с независимым возбуждением, у которого мощность управляющего сигнала в цепи возбуждения Ру=IуUу значительно меньше мощности выходного сигнала на нагрузку Рн=IнUн. Отношение мощности выходного сигнала к мощности управляющего сигнала называется коэффициентом усиления ЭМУ по мощности kу=Pн/Pу. Коэффициент усиления у простейшего ЭМУ небольшой (80—100), поэтому широкого применения такие ЭМУ не нашли. Наибольшее применение получили многоступенчатые ЭМУ, коэффициенты усиления которых достигают 10—12 тыс.

    В системах автоматического регулирования широко применяют ЭМУ с поперечным полем (амплидины), представляющие собой двух- или четырехполюсные генераторы постоянного тока со специальной конструкцией статора. На полюсах ЭМУ расположено несколько обмоток управления (ОУ).

    1. Способы описания САУ. Математическое описание, схематическое изображение. Структурная, функциональная схема.

    Первоочередной задачей теории автоматического управления при исследовании системы автоматического управления (САУ) является формализованное описание системы, т.е. составление её математической модели. Исходным описанием исследуемой системы является её техническое описание, содержащее принципиальные схемы, чертежи устройства и другую техническую документацию. На основе этой документации и необходимо разработать математическую модель исследуемой системы.

    Для составления математической модели САУ в теории автоматического управления используется структурный метод. При этом САУ представляется в виде соединений элементарных элементов, каждый из которых выполняет определенные функции по преобразованию сигналов в системе. Такое соединение изображается упрощенной схемой, которая может быть двух видов: функциональная и структурная.

    Функциональная схема – схема, в которой исследуемая система представляется в виде соединения функциональных элементов и каждому функциональному элементу САУ приписывается некоторая функция преобразования входного сигнала в выходной. Преобразуемые сигналы являются при этом реальными сигналами описываемой системы. Компонентами функциональной схемы являются функциональные элементы.

    Структурная схема – схема, в которой преобразование каждого сигнала описывается математически. Математические описания взаимосвязей между входными и выходными сигналами преобразующих элементов системы приписываются компонентам структурной схемы – структурным звеньям. В результате структурная схема является математическим описанием взаимосвязей между сигналами в исследуемой системе, т.е. математической моделью системы.

    Рассмотрим в качестве примера систему регулирования частоты вращения n(t) вала электродвигателя, построенную по схеме "генератор – двигатель" и используемую в системах автоматизированного электропривода. Целью управления в системе является поддержание постоянной частоты вращения n(t) вала электродвигателя Д при изменении нагрузки на его валу.

    Скорость вращения двигателя преобразовывается тахогенератором Тг в пропорциональное напряжение Uтг, которое сравнивается с напряжением задания Uз, задаваемым потенциометром Rз. Разность напряжений U усиливается усилителем У и подаётся на обмотку возбуждения генератора Г. При изменении величины напряжения возбуждения Uв изменяется выходное напряжение генератора Uг, подаваемое на электродвигатель, что вызывает изменение его частоты вращения.

    За счёт изменения напряжения в цепи якоря электродвигателя, при изменениях нагрузки на валу двигателя его частота вращения оставалась бы постоянной. В системе происходит автоматическая стабилизация скорости вращения вала электродвигателя. Для изменения заданной скорости вращения служит потенциометр Rз, который позволяет изменять напряжение задания Uз.

    На первом этапе применения структурного метода принципиальная схема системы заменяется упрощенной функциональной схемой. Функциональная схема позволяет проследить последовательность преобразования сигналов.

    На втором этапе применения структурного метода для каждого функционального элемента математически описывается связь в динамике между входным и выходным сигналами, т.е. с использованием дифференциального уравнения. Для описания используются известные физические законы, применимые к описываемому элементу с учётом его физической природы. При описании системы в качестве входного сигнала как элемента, так и всей системы в целом может рассматриваться любое внешнее воздействие. В качестве выходного сигнала рассматривается управляемая величина.

    Электронный усилитель с учётом того, что процессы протекают в нём во много раз быстрее процессов в электромеханических элементах системы, можно описать дифференциальным уравнением нулевого порядка (т.е. алгебраическим уравнением).

    Аналогичные дифференциальные уравнения (и операторы) можно получить и для других элементов системы. Заменяя функциональные элементы в функциональной схеме операторами этих элементов, получим структурную схему системы автоматического управления. Структурная схема состоит из структурных звеньев. Каждое структурное звено описывается его оператором.

    При описании функциональных элементов необходимо соблюдать условие ограничения порядка получаемого дифференциального уравнения. Этот порядок не должен быть выше второго. Если при описании получается более высокий порядок дифференциального уравнения, то элемент следует разбить на более простые элементы.

    Полученная структурная схема дает математическое описание САУ. Это описание учитывает параметры исследуемой системы. Вместо структурных схем для описания САУ могут применяться направленные графы. При этом вершины графа соответствуют сигналам системы, а дуги графа - операторам структурных звеньев.

    При описании САУ могут применяться как структурные схемы, так и графы. В настоящее время более широкое распространение имеет описание САУ при помощи структурных схем.

    1. Частотная и операторная передаточные функции.

    Одной из основных характеристик объекта управления, используемой в теории автоматического управления, является передаточная функция, записываемая в терминах преобразования Лапласа.

    Передаточной функцией объекта называется отношение преобразованного по Лапласу выхода объекта у(s) к преобразованному по Лапласу входу х(s) при нулевых начальных условиях.

    Передаточная функция определяется только внутренними свойствами системы, является функцией комплексного переменного и обозначается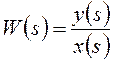



    Передаточная функция характеризует динамику объекта по каналу, связывающему конкретный вход и выход объекта.



    Рисунок - Примеры различных объектов: а) с одним входом и одним выходом; б) двумя входами и одним выходом; в) двумя входами и двумя выходами

    Если объект имеет несколько входов и выходов, то он характеризуется несколькими передаточными функциями.

    Передаточная функция характеризует динамику линейного объекта. Если задано дифференциальное уравнение, то для получения передаточной функции необходимо преобразовать дифференциальное уравнение по Лапласу и из алгебраического уравнения найти отношение   .

    Дифференциальное уравнение объекта представляется в виде

    any(n)(t)+an−1y(n–1)(t)+…+a1y¢(t)+a0y(t)=bmx(m)(t)+bm−1x(m-1)(t)+…+b1x¢(t)+b0x(t),

    где an, …, a0; bm, …, b0 – постоянные коэффициенты.

    После преобразования по Лапласу при нулевых начальных условиях

    ansny(s)+an−1sn–1y(s)+...+a0y(s)=bmsmx(s)+bm−1sm–1x(s)+...+b0x(s),

    (ansn+an−1sn–1+...+a1s+a0)y(s)=(bmsm+bm−1sm–1+...+b1s+b0)x(s),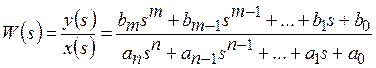

    .

    Если известна передаточная функция объекта, то изображение выхода объекта у(s)= W(s)x(s).

    Передаточная функция является отношением полиномов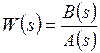

    ,

    где B(s)=bmsm+bm−lSm–l+...+b1s+b0;

    A(s)=ansn+an−lSn–l+…+a1s+a0y.

    Для реальных физических объектов степень полинома В(s)всегда меньше или равна степени полинома A(s), то есть m ≤ n.

    Для переходной функции входной сигнал x(t) = 1(t), 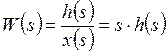  , выходной сигнал y(t) = h(t), y(s) = h(s), и тогда передаточная функция равна

    .

    Из этого выражения может быть получено выражение для переходной функции

    .

    Если известно выражение для весовой функции, то входной сигнал x(t) = δ(t), x(s) = 1, выходной сигнал w(t) и передаточная функция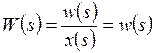

    ,

    является преобразованием Лапласа от весовой функции.

    Из полученных выражений имеем w(s) = s×h(s), то есть w(t) = h¢(t).

    1. Временные характеристики САУ. Переходная, весовая функции.

    Временной характеристикой системы называется закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.

    К основным временным характеристикам относятся переходная функция и функция веса.

    Типовые воздействия. В качестве типовых воздействий при исследовании систем используются:

    – единичная функция;

    – единичный импульс;

    – линейно – растущее воздействие;

    – квадратичное воздействие;

    – гармоническое воздействие.

    Переходная функция. Переходная функция h(t) – реакция системы на единичное воздействие при нулевых начальных условиях.

    Весовая функция. Весовая функция k(t) – реакция системы на единичный импульс при нулевых начальных условиях.

    Методы определения временных характеристик

    1. Классический метод (основан на решении дифференциальных уравнений).

    2. Операторный метод, использующий разложение на простые дроби.

    3. Операторный метод, использующий вычеты.

    4. Метод аналогового и цифрового моделирования.

    5. Метод трапеций.

    1. Частотные характеристики САУ, в т.ч. логарифмические.

    Частотными характеристиками называются зависимости, характеризующие реакцию звена на гармоническое входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена. Частотные характеристики, определяют зависимость между амплитудой и фазой входного и выходного гармонических сигналов при изменении частоты входного сигнала.

    Если на вход линейного звена подать гармоническое воздействие:



    где X0 - амплитуда,

    ω - угловая частота, имеющая размерность [рад/с] или [c-1],

    то на выходе звена в установившемся режиме будет также гармоническая функция той же частоты, но другой амплитуды Y0 и сдвинутая по фазе относительно входной величины на угол ψ:

     .

    Связь между выходной гармоникой и входной устанавливается с помощью частотной передаточной функции звена W(jω).

    Частотная передаточная функция представляет собой отношение изображений по Фурье выходного и входного сигналов при нулевых начальных условиях и равных нулю воздействиях на остальных входах: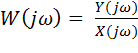

     

    Из сравнения преобразований Фурье и Лапласа следует, что частотную передаточную функцию звена легко получить из его передаточной функции путем замены s на jω(подстановка Фурье), т.е.



    Запись W( jω) означает, что в передаточную функцию W(s) подставляется чисто мнимое число s = jω , где j =   .

    Зависимость отношения амплитуды выходного сигнала к амплитуде входного сигнала при фиксированной частоте называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w).

    Сдвиг фаз между входным и выходным сигналами при фиксированной частоте называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w).

    Амплитудная фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости в полярных координатах и представляет собой геометрическое место концов векторов (годографов), соответствующих частотной передаточной функции W(jω) при изменении частоты от нуля до бесконечности.

    Полученные точки соединяются затем плавной кривой. АФЧХ строится как для положительных, так и для отрицательных частот. При замене в W(jω) ω на -ω получается сопряженная комплексная величина. Поэтому АФЧХ для отрицательных частот является зеркальным отображением относительно вещественной оси АФЧХ для положительных частот.

    Как видим, (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси абсцисс.

    В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) : логарифмическая амплитудная ЧХ (ЛАЧХ) L( ) и логарифмическая фазовая ЧХ (ЛФЧХ)  ( ).

    Они получаются путем логарифмирования передаточной функции:



    ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L( ) = 20lgA( ). Величина L( ) откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так как

    lg(P2/P1) = lg(A22/A12) = 20lg(A2/A1).

    По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой. Так как lg(0) = -  , то ось ординат проводят произвольно.

    ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси  . Величина  ( ) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -       +  .

    ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.

    1. Пропорциональное звено. Диф. уравнение, передаточная функция, все временные и частотные характеристики. Примеры реализации.
    1   2   3   4

    написать администратору сайта