ответы на вопросы. тау. Экзаменационные вопросы по предмету тау
 Скачать 317.1 Kb. Скачать 317.1 Kb.
|
Звено апериодическое второго порядка.Дифференциальные уравнения таких звеньев имеют общий вид а передаточная функция – W(p) = K / (T22 p2 + T1 p + 1). В зависимости от соотношения постоянных времени Т1 и Т2 : а) Если 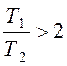 , то звено называется апериодическим второго порядка. Переходной процесс представляет собой S-образную кривую с перегибом в точке О (рис. 6.10). , то звено называется апериодическим второго порядка. Переходной процесс представляет собой S-образную кривую с перегибом в точке О (рис. 6.10).Примеры апериодического звена второго порядка: а) последовательное соединение двух пневматических емкостей, если входная величина х = Рпит, а выходная величина – давление во второй емкости у = Р ; б) двойная электрическая RC–цепочка. Колебательное звено. Если 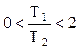 , то звено называется колебательным. , то звено называется колебательным.Дифференциальное уравнение звена обычно представляется в виде где x – коэффициент затухания, 0 < x < 1. При этом корни характеристического уравнения комплексные. Переходная характеристика звена представляет собой периодический сходящийся процесс, описываемый формулой 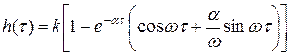 , ,где a = x / T, Примерами колебательных звеньев могут служить (рис. 6.13): а) электрический колебательный RCL–контур (R – активное сопротивление, C – емкость, L – индуктивность); б) упругая механическая передача, которая состоит из входного 1 и выходного 2 валов, упругого элемента 3, маховика 4 и демпфера 5, оказывающего сопротивление вращению вала. Входная величина х – угол поворота входного вала j1, выходная величина у – угол поворота выходного вала j2. Консервативное звено. Если Т1 = 0, то есть нет демпфирования, имеем консервативное звено 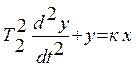 . .Это звено получается при мнимых полюсах передаточной функции и его можно рассматривать как частный случай колебательного звена при Ь = 0. Таким образом, консервативное звено – это идеальное колебательное звено, в котором нет рассеивания энергии (постоянная времени Т2 = 0) и колебания не затухают. Переходная характеристика представляет собой гармонические незатухающие колебания (в природе такого звена нет). Интегрирующие звенья В интегрирующих звеньях выходная величина пропорциональна интегралу по времени от входной величины. В отличие от позиционных звеньев интегрирующие звенья не приходят к установившемуся новому состоянию, а их выходная величина имеет тенденцию к неограниченному увеличению. Таким образом, интегрирующим называют звено, у которого выходная величина пропорциональна интегралу от входной величины. Дифференциальное уравнение интегрирующего звена Ему равноценно интегральное уравнение где K - коэффициент пропорциональности. Электрический конденсатор можно рассматривать как интегрирующее звено, если за выходную величину рассматривать напряжение. Передаточная функция интегрирующего звена имеет вид Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования. Интегрирующим звеном является также обычный гидравлический демпфер. Входной величиной здесь является сила F, действующая на поршень, а выходной — перемещение поршня х2. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил). Дифференцирующее звенья Дифференцирующее звено реализует функцию дифференцирования входного сигнала. Для этого звена выходной сигнал пропорционален скорости изменения входного сигнала. Уравнение и передаточная функция звена: 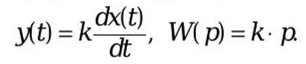 Выходная величина пропорциональна скорости изменения входной величины. Если входная и выходная величины имеют одинаковую размерность, то коэффициент кизмеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена. Выражения для основных функций: 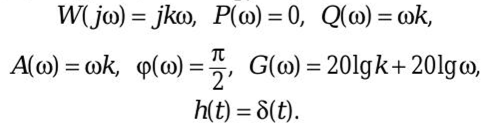 Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена являются обратными передаточной функции и соответствующим характеристикам интегрирующего звена. Логарифмические частотные характеристики рассматриваемого звена приведены на рис. 3.2а. При построении ЛАЧХ удобно отложить точку с координатами С(со) =20, 1до) = 1, провести через нее прямую с наклоном плюс 20 дБ/дек, затем отложить на оси С(со) отрезок С0 = 201дк (поскольку, как правило, к< 1, точка во будет находиться ниже оси 1дсо) и провести параллельную прямую. О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить мгновенный скачок выходной величины бесконечной амплитуды. Реальные дифференцирующие звенья обладают конечной инерционностью, вследствие чего осуществляемое ими дифференцирование не является точным. Структурная схема САУ.(условные обозначения на схемах) Структурной схемой системы автоматического управления называют графическое представление ее математической модели в виде соединений звеньев, изображаемых в виде прямоугольников или окружностей (для сумматора), с указанием входных и выходных переменных. Обычно внутри прямоугольника указывается условное обозначение оператора, изображаемого им звена, а сам оператор в виде передаточной функции или дифференциального уравнения задается вне структурной схемы. В сумматоре входные переменные складываются. Однако если перед каким-либо входом стоит знак минус, переменная по этому входу вычитается (складывается со знаком минус). При изображении структурной схемы САУ применяют следующие обозначения ее элементов. Блок с указанной внутри него динамической характеристикой элемента (как правило, передаточной функцией). Сумматор, выход которого равен сумме входных сигналов. Знак каждого сигнала может быть указан возле соответствующего входа или закрашиванием секторов внутри сумматора; при этом сигналы, подходящие к закрашенным секторам, суммируются со знаком «-». Интегратор может быть условно обозначен символом интегрирования или как другие блоки - передаточной функцией. Структурная схема может быть построена как на основе дифференциальных уравнений, так и передаточных функций элементов САУ. При этом существует множество вариантов решения. Возможен и обратный переход, т. е. на основе структурной схемы можно получить дифференциальное уравнение системы, причем в данном случае решение будет единственным. Решение обеих задач связано с преобразованием структурных схем. Правила преобразования структурных схем В тех случаях, когда структурная схема оказывается слишком сложной, например, содержит перекрестные связи, ее упрощают, пользуясь правилами преобразования структурных схем. Смысл этих правил состоит в переносе элементов структурной схемы из одного положения в другое, так чтобы при этом сохранялась эквивалентность структурных схем. 1. Перенос узла через звено. 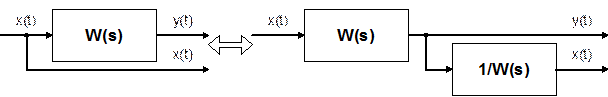 Чтобы перенести узел через звено с передаточной функцией W(s), необходимо включить в линию, не проходящую через звено (выход 2), дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Действительно, сигнал у(t) после такого переноса не изменится, а сигнал на выходе 2 будет равен: Х(s)·W(s)·1/W(s) = Х(s), т.е. он совпадает с исходным сигналом х(s). 2. Перенос звена через узел. 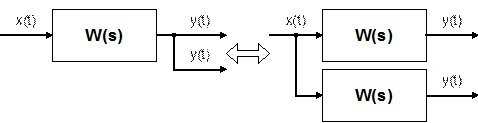 Чтобы перенести звено с передаточной функцией W(s) через узел, необходимо включить в обе линии звенья с передаточной функцией W(s). Легко убедиться, что эквивалентность структурных схем при этом сохраняется. 3. Перенос сумматора через звено. 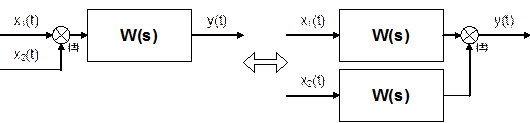 Сразу отметим, что данное правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения, т.к. элемент сравнения можно рассматривать как сумматор с инвертированным входом. Чтобы перенести сумматор через звено с передаточной функцией W(s), необходимо к обоим входам на сумматор добавить дополнительный элемент – звено с передаточной функцией W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·[X1(s) ± X2(s)]; выходной сигнал на преобразованной схеме равен: Y(s) = W(s)X1(s) ± W(s)X2(s), т.е. выходные сигналы совпадают. 4. Перенос звена через сумматор.  Это правило преобразования структурных схем также применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести звено с передаточной функцией W(s) через сумматор, необходимо в линию без звена (вход 2) включить дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·X1(s) ± X2(s); выходной сигнал на преобразованной схеме равен: Y(s) = W(s)·[X1(s) ± 1/W(s)·X2(s)] = W(s)·X1(s) ± X2(s), т.е. выходные сигналы совпадают. 5. Перенос узла через сумматор. 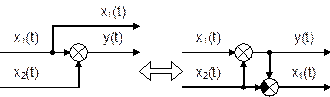 Чтобы перенести узел через сумматор, необходимо в схему включить дополнительный элемент – элемент сравнения. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t) и х1(t) = у(t) – х2(t) = х1(t) + х2(t) – х2(t). 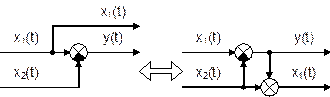 При применении этого правила преобразования структурных схем для переноса узла через элемент сравнения в схему необходимо включить дополнительно не элемент сравнения, а сумматор. Эквивалентность этих схем также легко проверить: у(t) = х1(t) – х2(t) и х1(t) = у(t) + х2(t) = х1(t) – х2(t) + х2(t). 6. Перенос сумматора через узел. 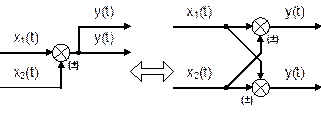 Это правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести сумматор через узел, необходимо в схему включить дополнительный сумматор. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t). 7. Перенос сумматора через сумматор. 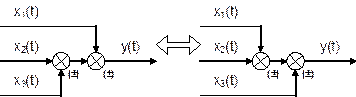 Это правило преобразования структурных схем фактически реализует правило коммутативности сложения в математике – от перестановки мест слагаемых сумма не изменяется. Оно, разумеется, применимо как к сумматорам, так и к элементам сравнения. 8. Перенос звена через звено.  Это правило преобразования структурных схем фактически реализует правило коммутативности умножения в математике – от перестановки мест множителей произведение не изменяется. Обратные связи САУ, виды, примеры. Обратная связь – это процесс передачи воздействия или подача на вход АУУ управляемой велечины или её части посредством первичного измерительного преобразователя установленного на выходе системы для формирования управляющего воздействия. Обратная связь может быть главной, отрицательной и положительной. Когда воздействия по цепи обратной связи складывается м задающим воздействием, то обратная связь называется положительной. Обр. связь образуемая регулятором по отношению к управляемому объекту называется главной – связь в САУ между входом и выходом объекта, образующая замкнутый контур управления. И обратные связи в самом регуляторе называются местными - связь между входом и выходом любого функционального элемента АР. Обр. связь может быть жесткой и гибкой. Жесткая (ОС) действует в переходном и установившихся режимах. Гибкая – только в неустановившемся режиме работы объекта. Наибольшее распространение в технике получил принцип обратной связи. Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). И уже не важно, какие возмущения действуют на ОУ. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Связь выхода ОУ с его входом называется главной обратной связью (ОС). В частном случае ЗУ формирует требуемое значение выходной величины yо(t), которое сравнивается с действительным значением на выходе САУ y(t). Отклонение e = yо-y с выхода сравнивающего устройства подается на вход регулятора Р, объединяющего в себе УУ, УО, ЧЭ. Если e0, то регулятор формирует управляющее воздействие u(t), действующее до тех пор, пока не обеспечится равенство e = 0, или y = yо. Так как на регулятор подается разность сигналов, то такая обратная связь называется отрицательной, в отличие от положительной обратной связи, когда сигналы складываются. Такое управление в функции отклонения называется регулированием, а подобную САУ называют системой автоматического регулирования (САР). Наличие усилителя говорит о том, что данная САР является системой непрямого регулирования, так как энергия для функций управления берется от посторонних источников питания, в отличие от систем прямого регулирования, в которых энергия берется непосредственно от ОУ, как, например, в САР уровня воды в баке. Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации, что позволяет объединить достоинства обоих принципов: быстроту реакции на возмущение принципа компенсации и точность регулирования независимо от природы возмущений принципа обратной связи. |
