Дифференциальные уравнения. Задача_4958_дифференциальные_уравнения. Решение Выразим производную Теперь разделим переменные Проинтегрируем обе части Мы получили общий интеграл дифференциального уравнения. При желании можно выразить Найти решение задачи Коши Решение
 Скачать 0.54 Mb.
|
 Решение: Выразим производную: 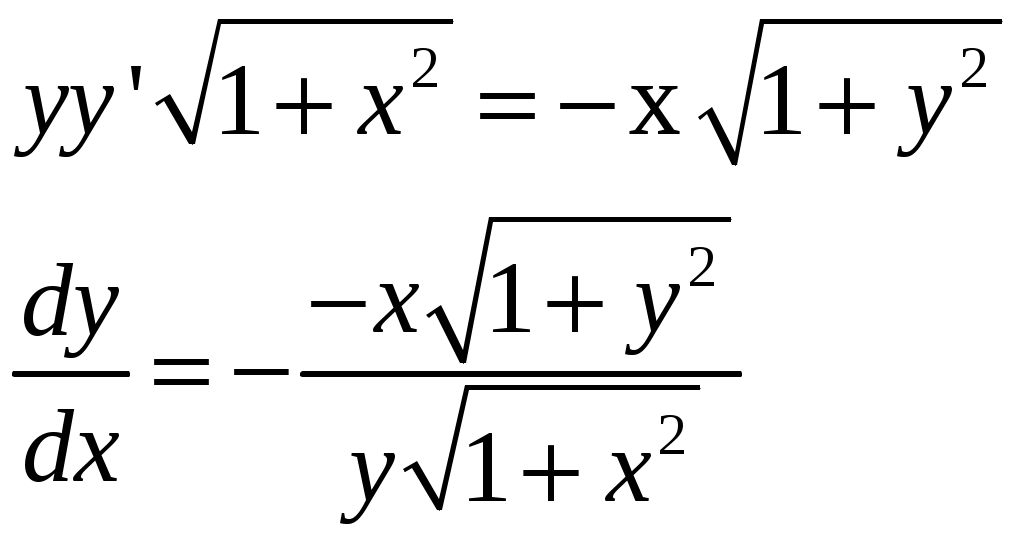 Теперь разделим переменные: 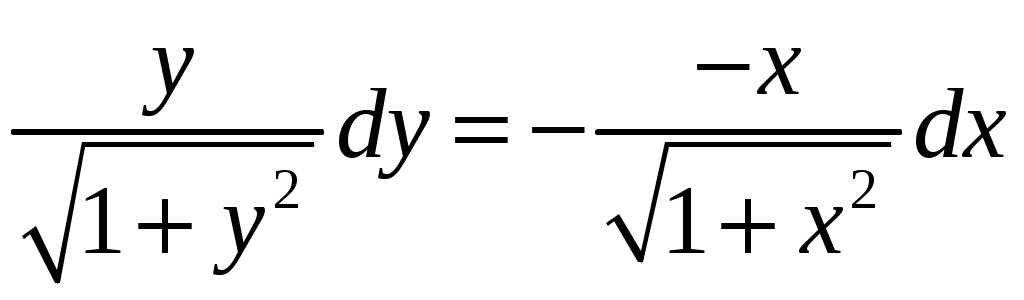 Проинтегрируем обе части: 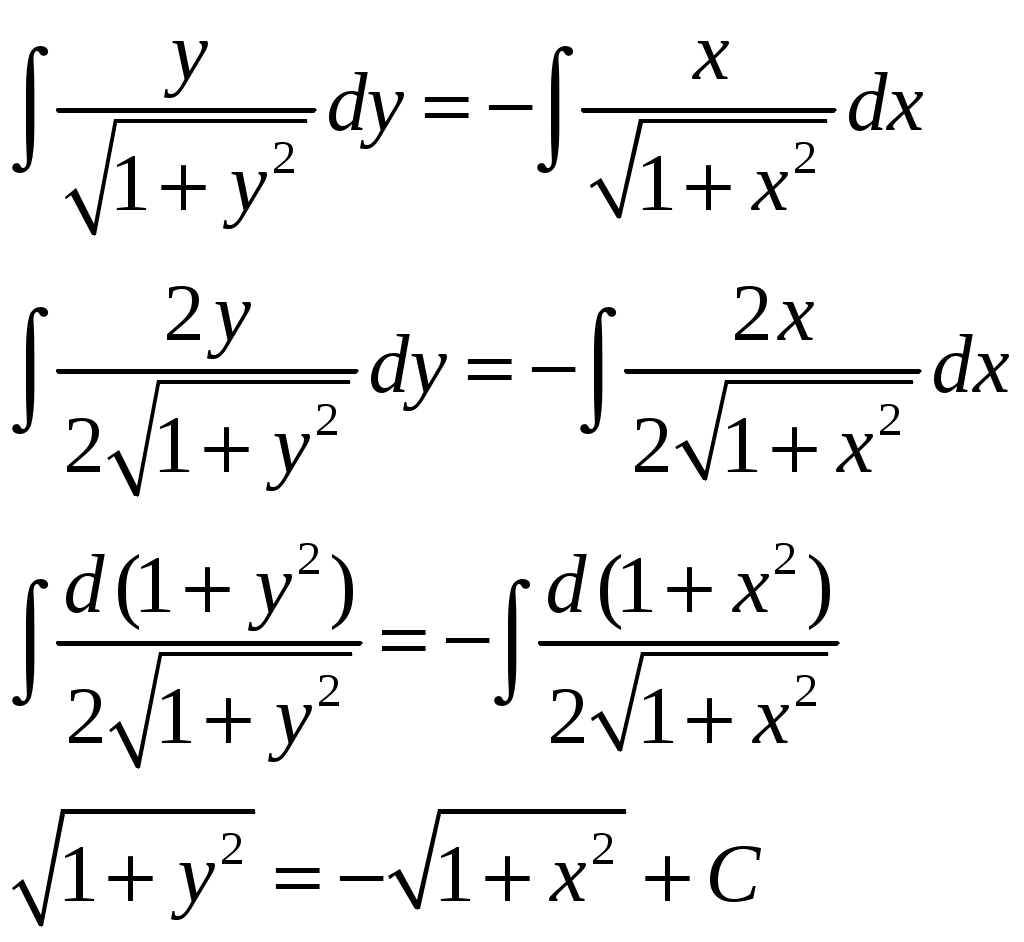 Мы получили общий интеграл дифференциального уравнения. При желании можно выразить  : Найти решение задачи Коши  Решение: Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Общий вид таких уравнений следующий:  В нашем случае и  , и  .Решить такое уравнение можно домножив обе части уравнения на интегрирующий множитель, который можно найти по формуле:  Если мы это сделаем, мы получим в левой части полный дифференциал:   И получим уравнение с разделяющимися переменными. Найдем интеграл   В интегрирующем множителе нам не важна константа интегрирования. Найдем Q(x) для наших данных: 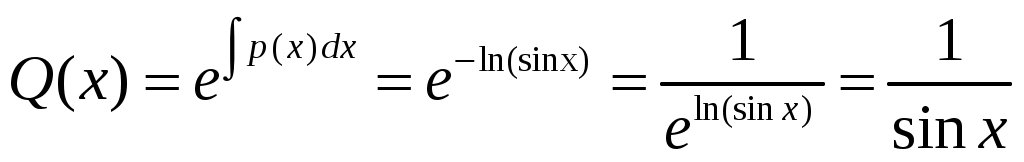 Домножим обе части уравнения на интегрирующий множитель:  Левая часть получилась равна 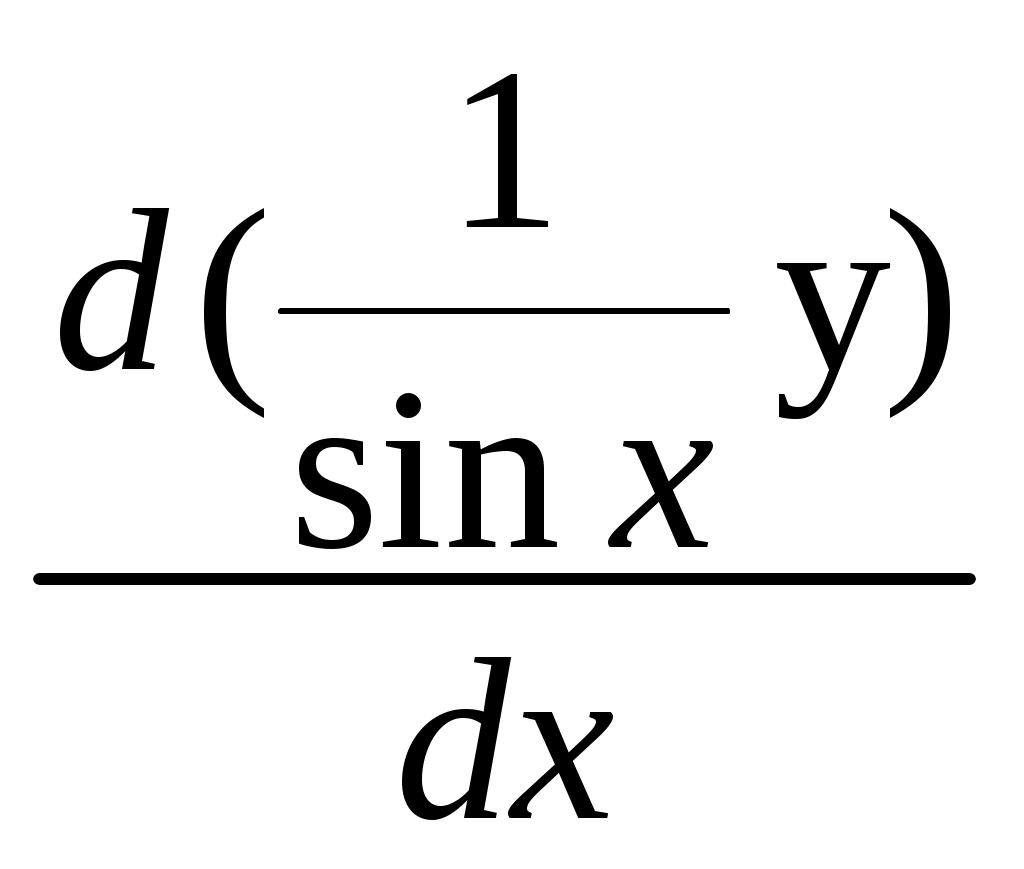 . Проверим это: Следовательно, левую часть можно свернуть: 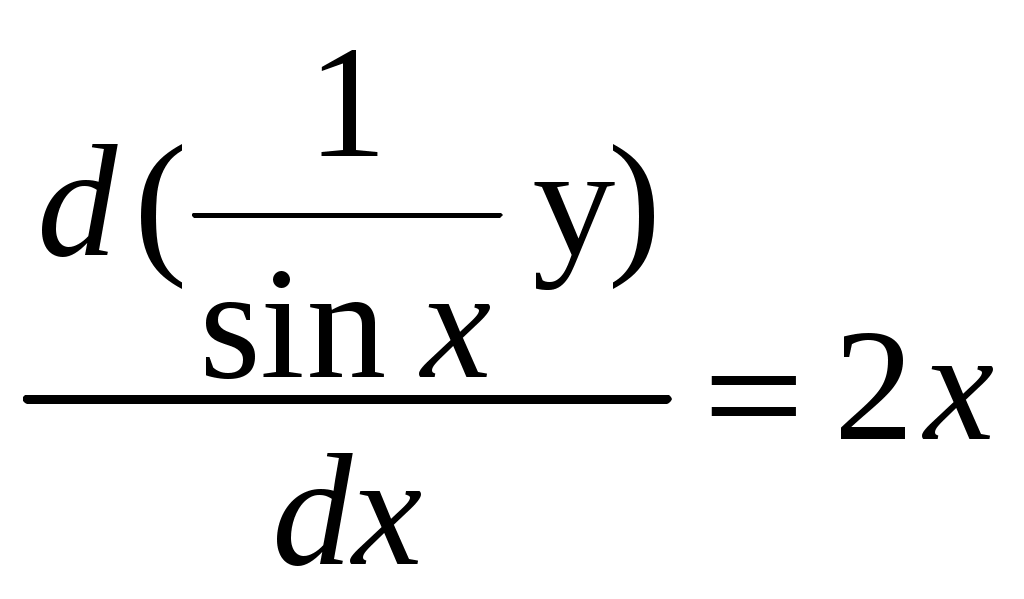 .Перенесем  в правую часть уравнения: Проинтегрируем обе части: 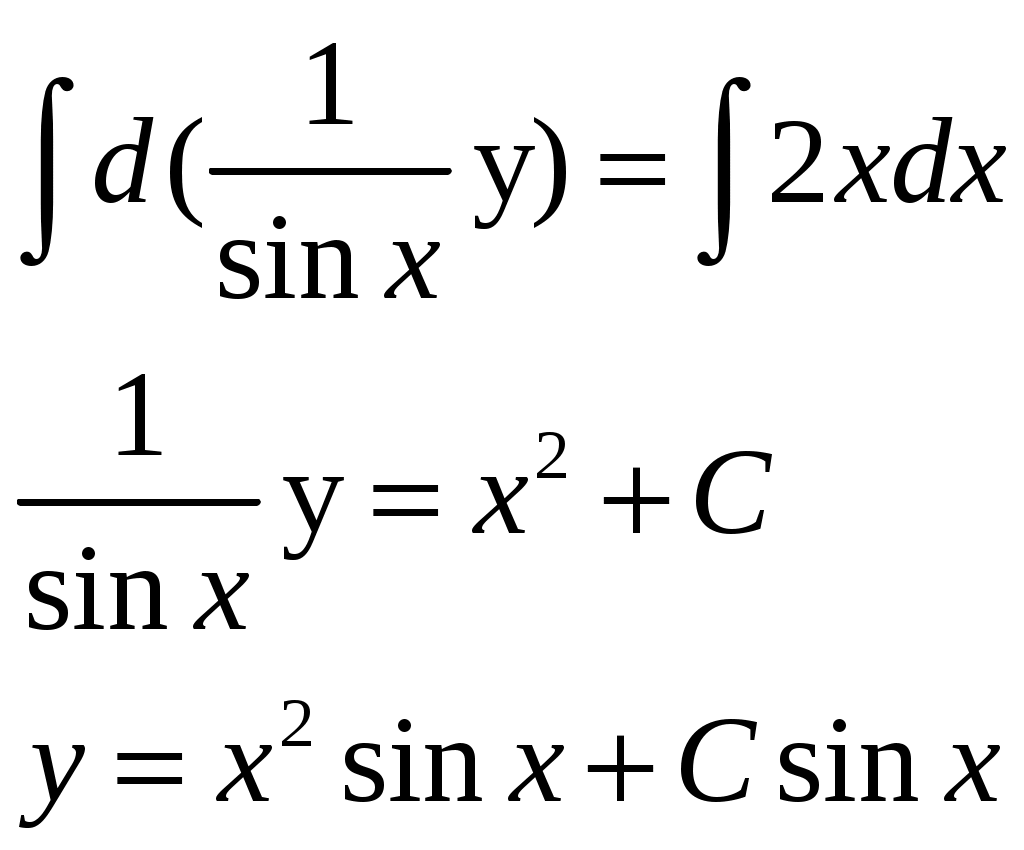 Для решения задачи Коши подставим начальные условия:  Следовательно, решением задачи Коши будет  Найти общий интеграл дифференциального уравнения 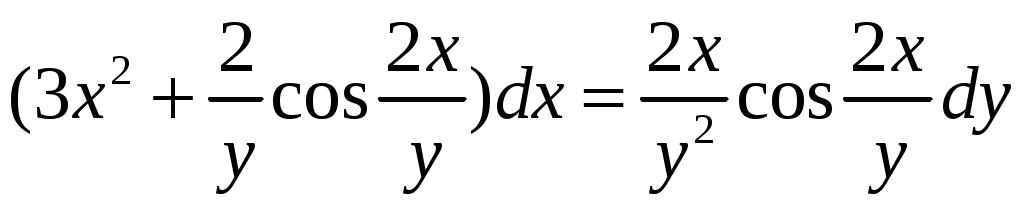 Решение: Преобразуем наше уравнение  Обозначим  ;  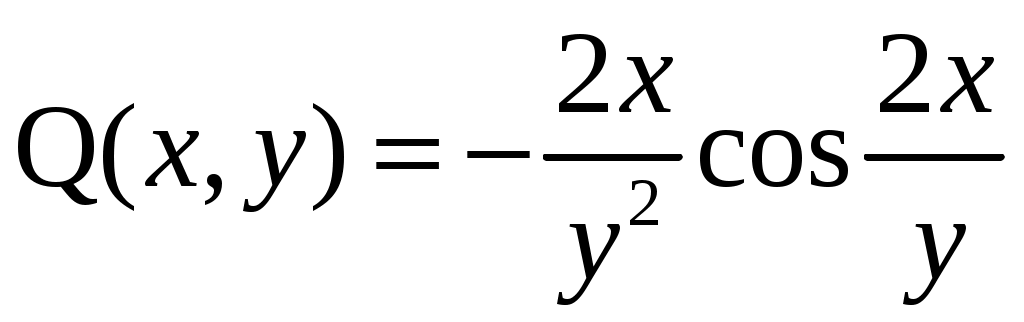, тогда наше уравнение будет иметь вид: Наше уравнение похоже на уравнение в полных дифференциалах, но чтобы это доказать, необходимо показать равенство частных производных. Найдем их: 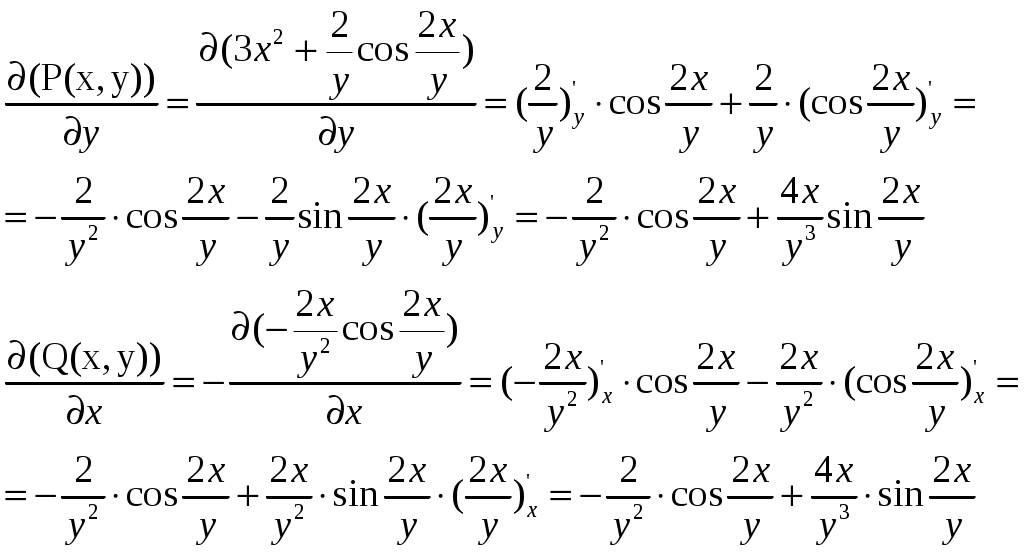 Таким образом, у нас уравнение в полных дифференциалах, которое имеет вид 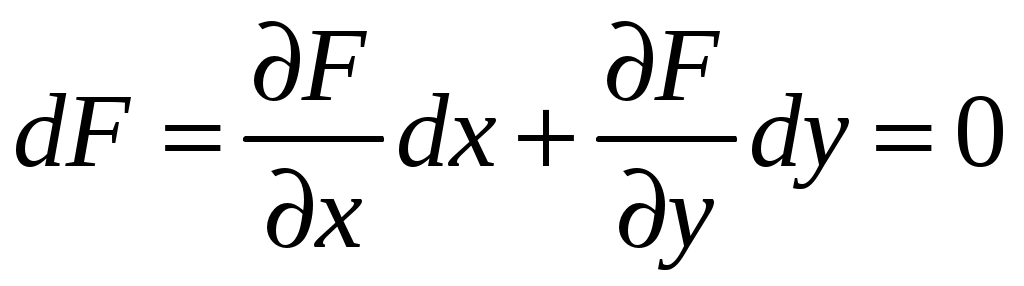 . Нам известны две частных производных некоторой функции F, и нам нужно ее найти. Получаем систему уравнений: Проинтегрируем первое выражение:  Дифференцируем переменную F по y:  Сравним два полученных выражения: 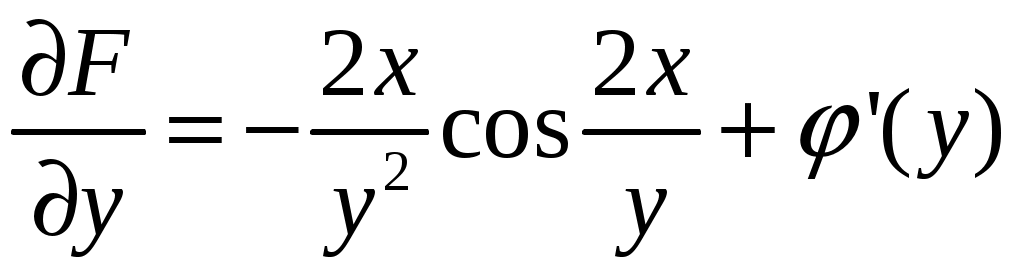 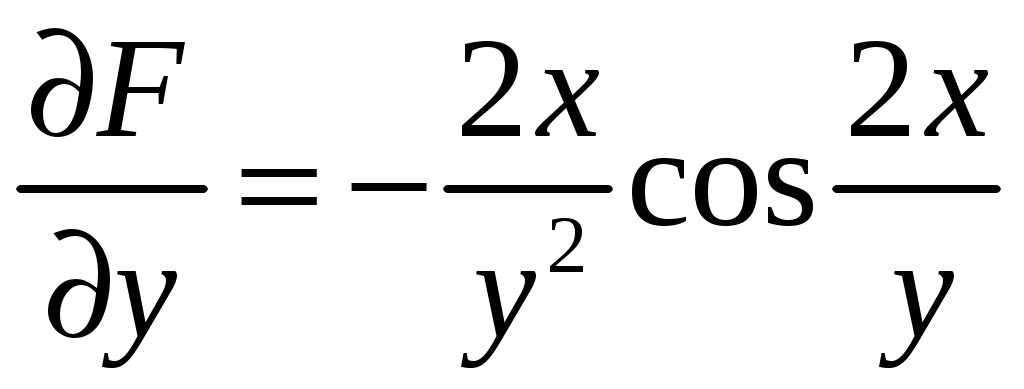 Откуда сразу видно, что  Проинтегрируем данное выражение:  Следовательно, мы имеем: 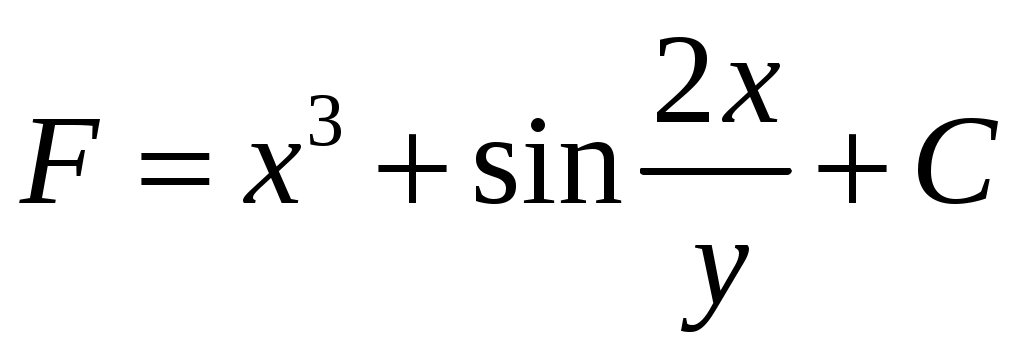 Тогда ответ на задачу можно записать в виде: 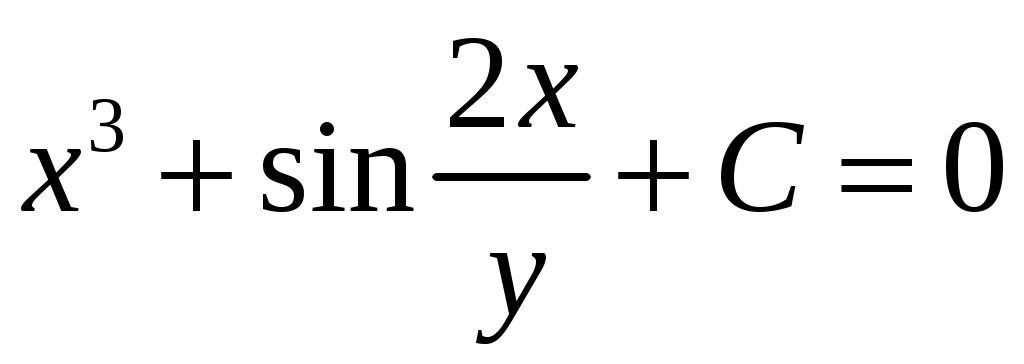 Либо можно выразить 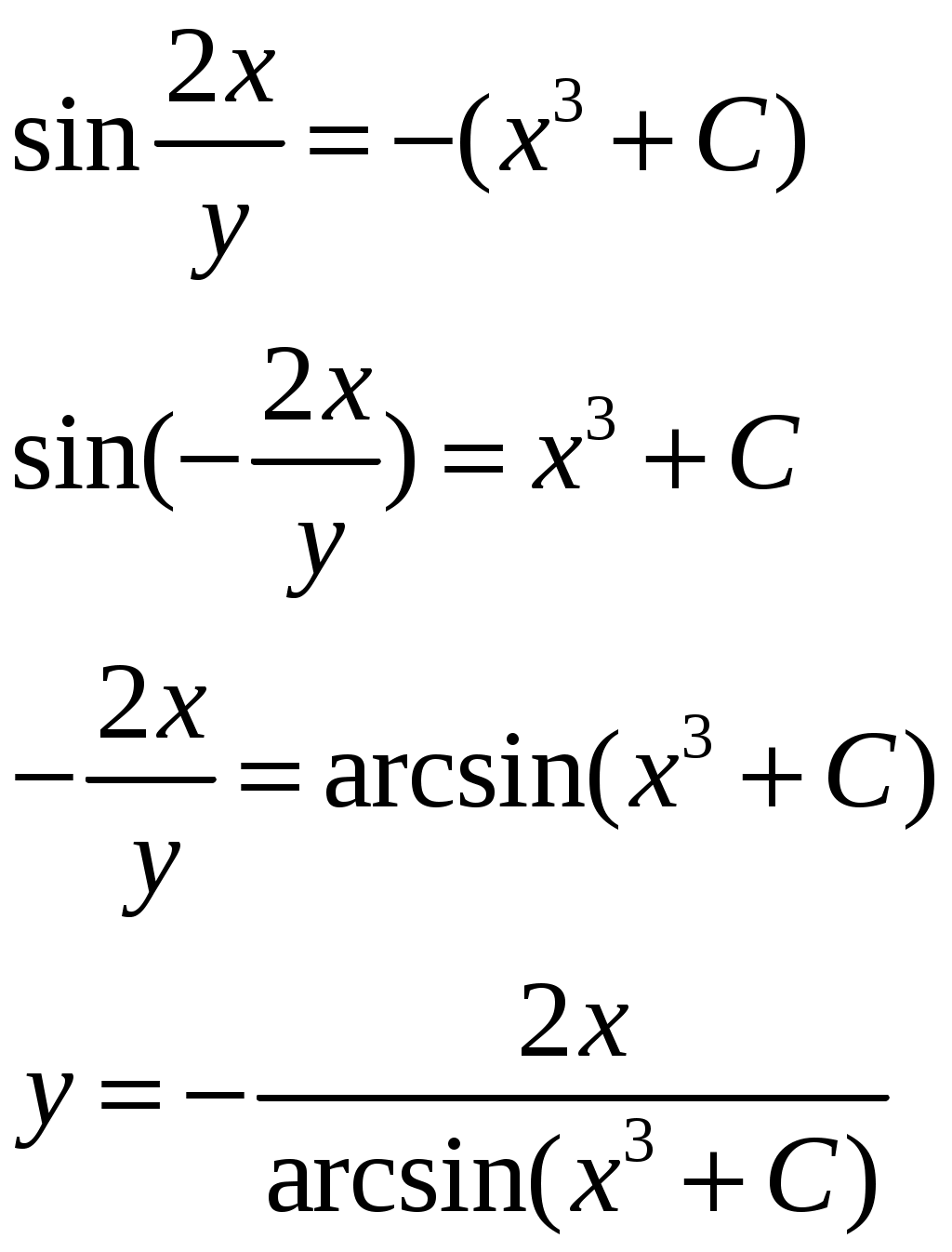: Мы воспользовались тем, что синус это нечетная функция. Найти общее решение дифференциального уравнения  Решение: Введем новую переменную 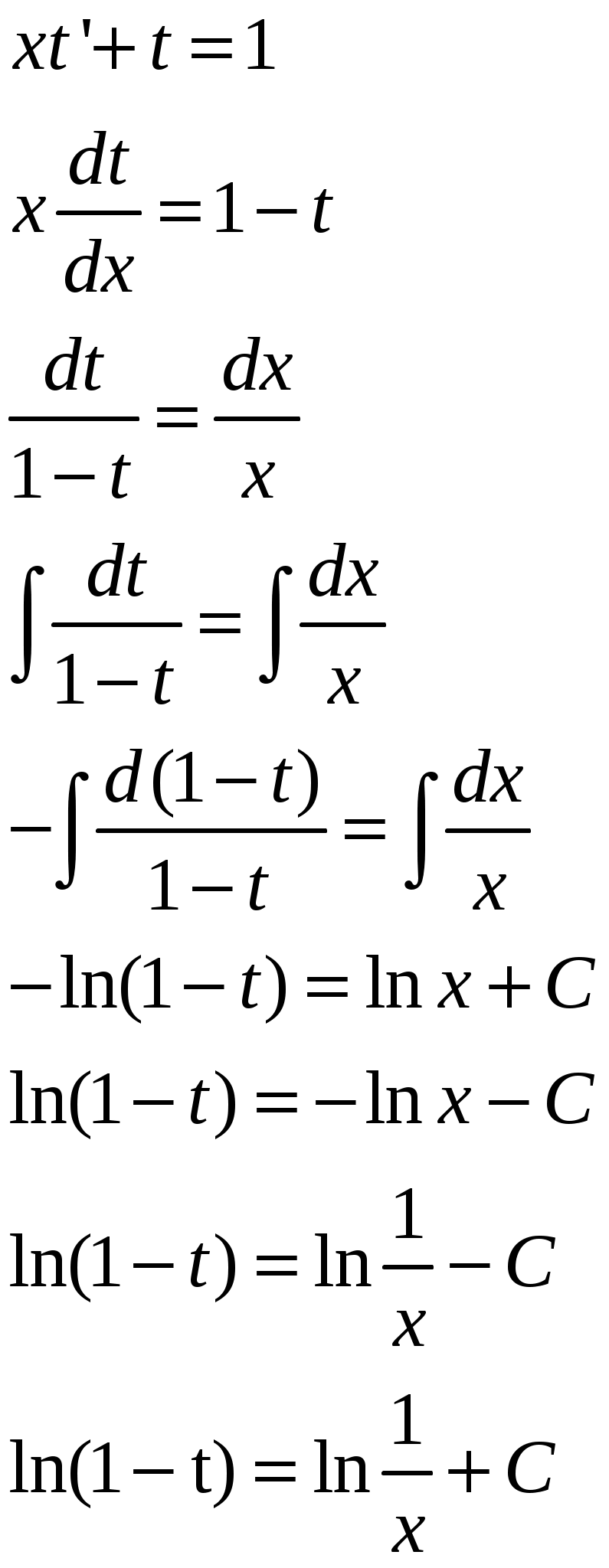 . Получим: Мы воспользовались тем, что константа с обратным знаком все равно остается константой.  Мы воспользовались тем, что экспонента в степени константы все равно равна константе. 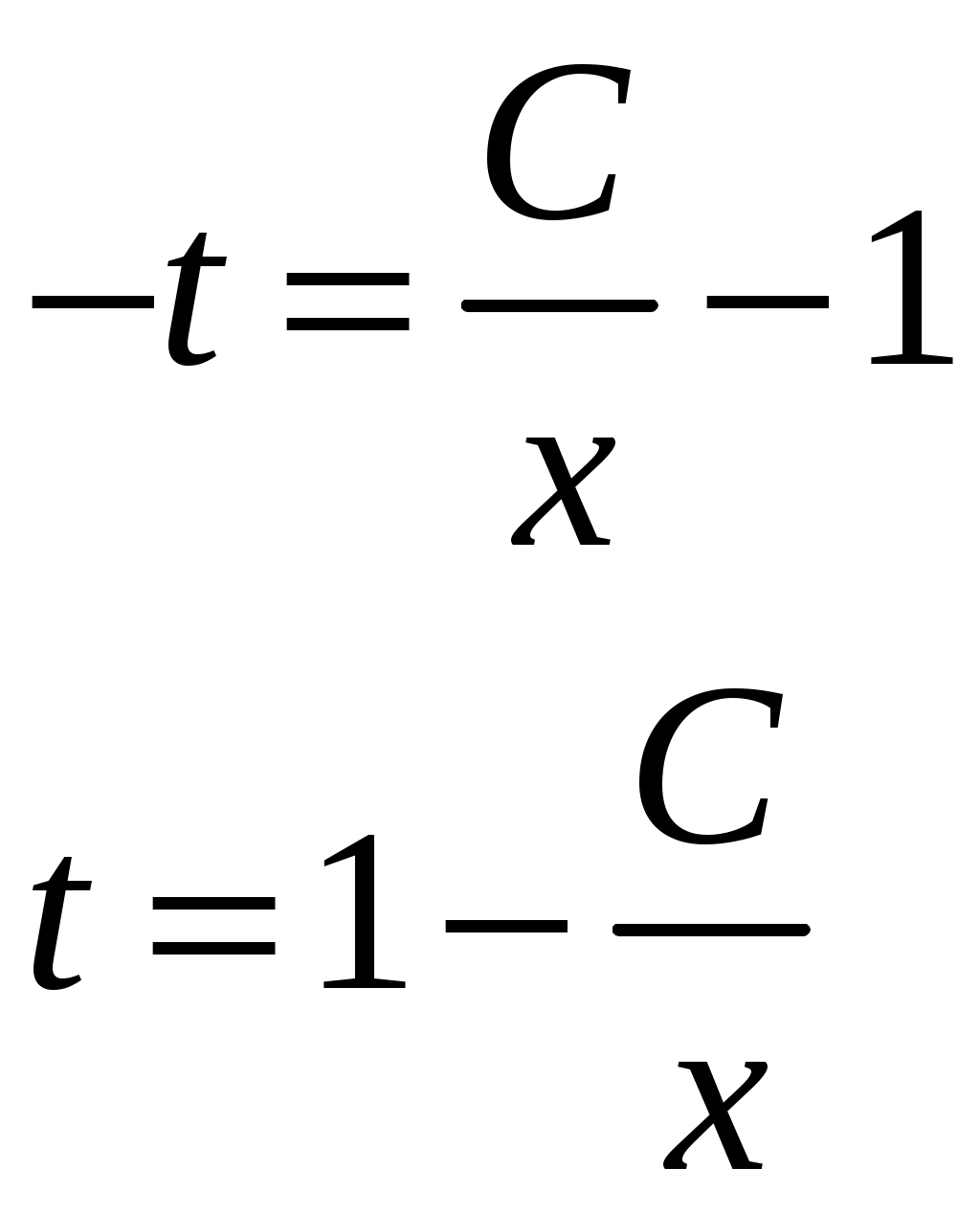 Теперь вернемся к переменной и два раза проинтегрируем уравнение: Мы воспользовались тем, что  все равно остается константой.Найти решение задачи Коши  Решение: Введем новую переменную  , тогда  . Получаем: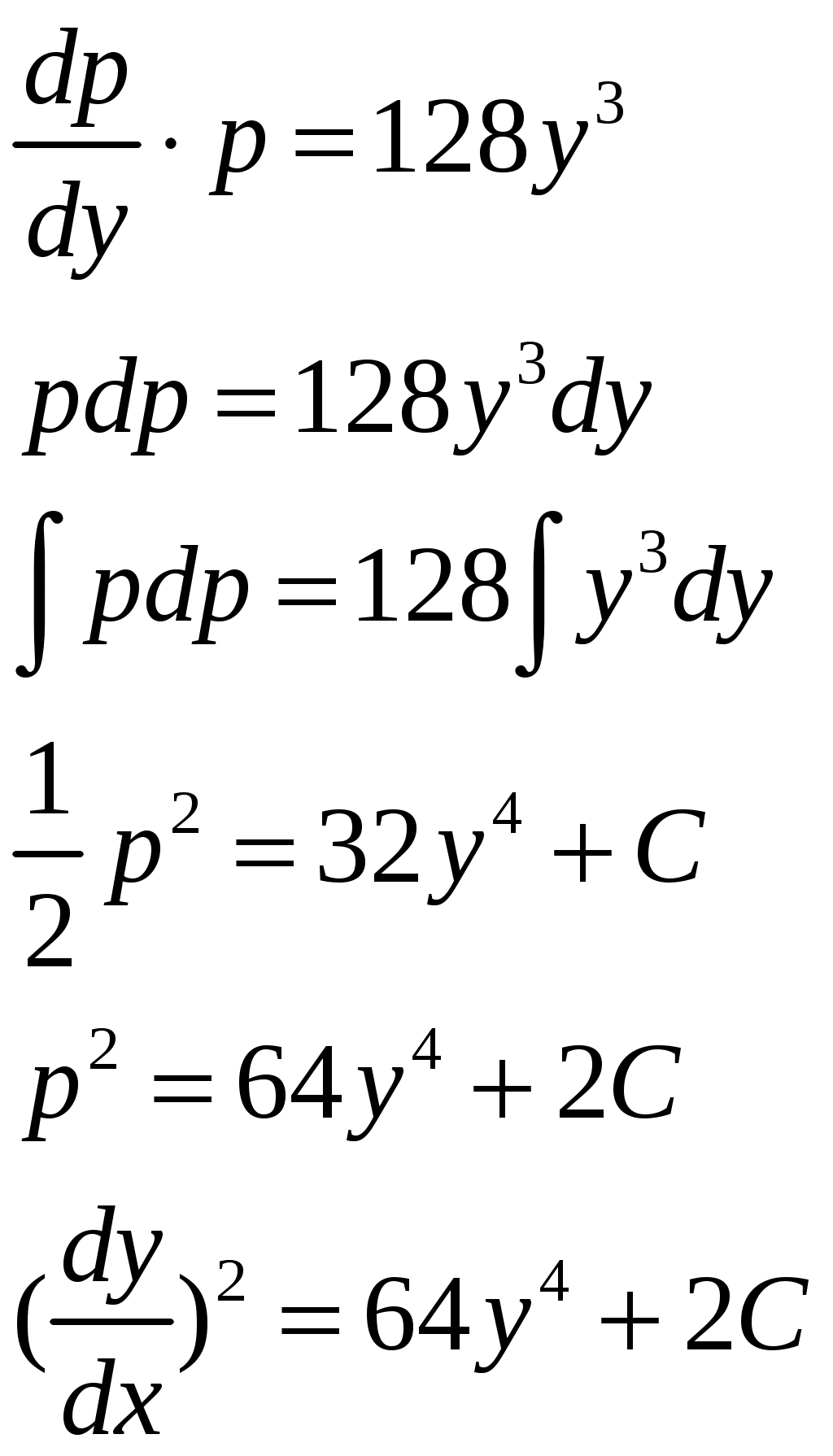 Подставим начальное условие 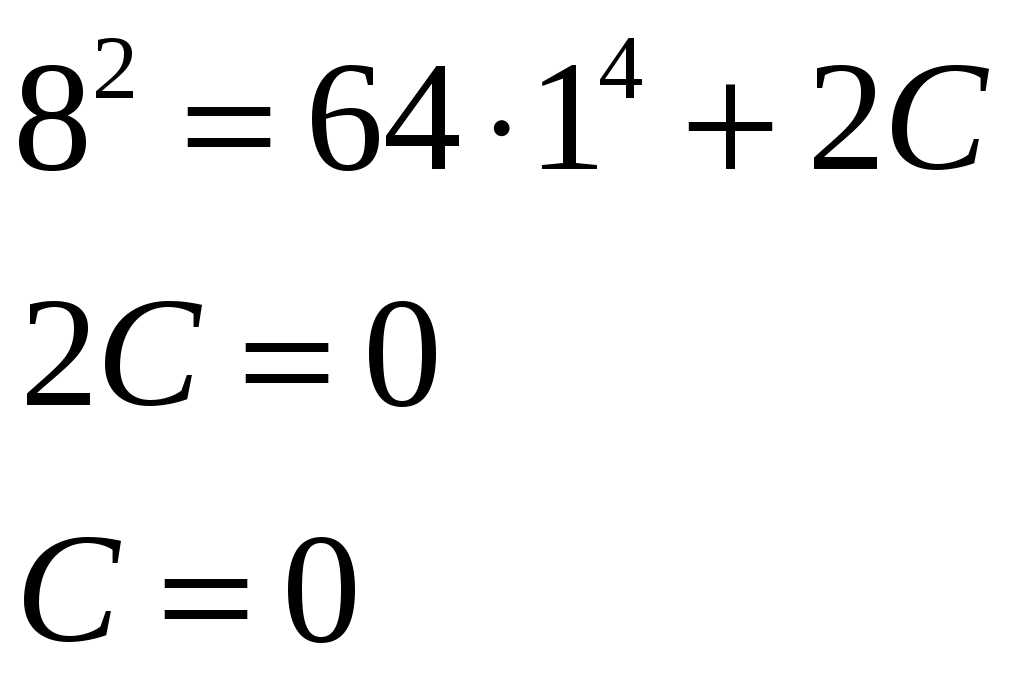 , и получим: То есть, получаем, что 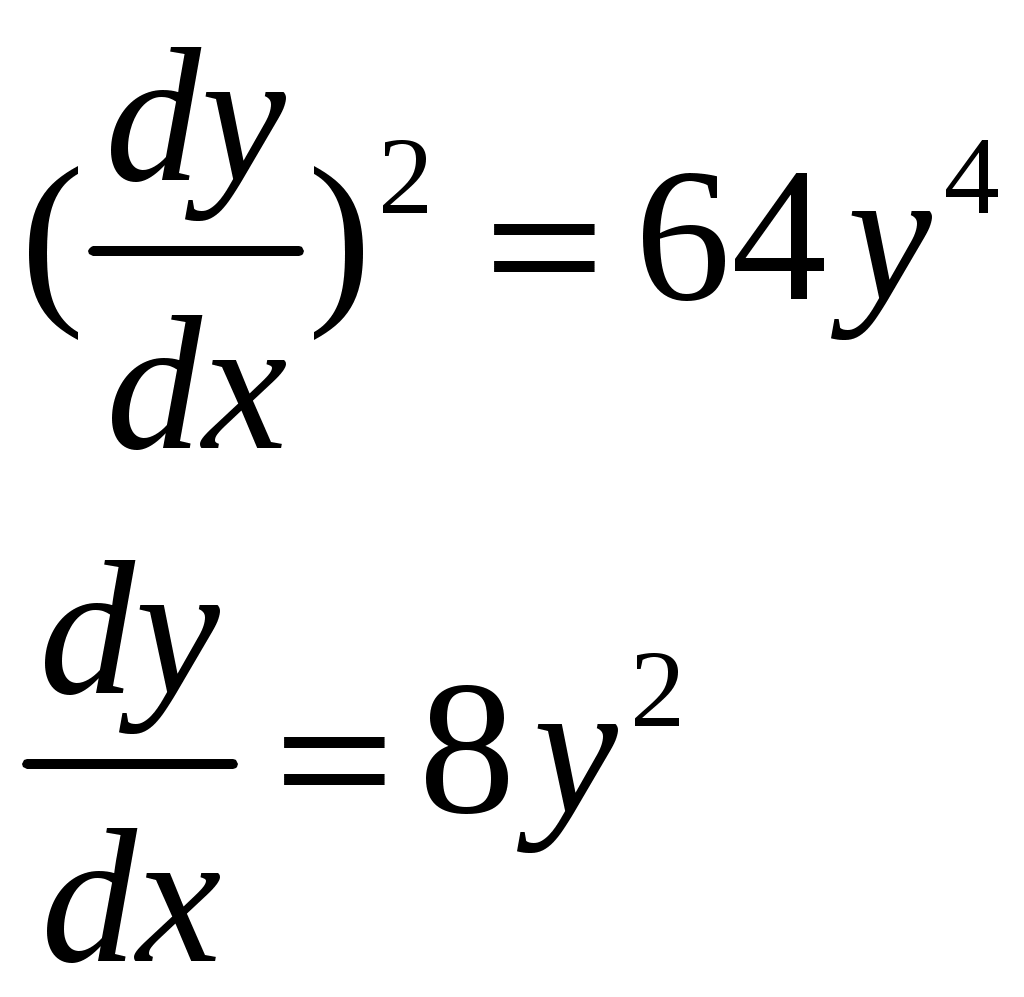 Мы взяли только положительный корень, так как по начальным условиям 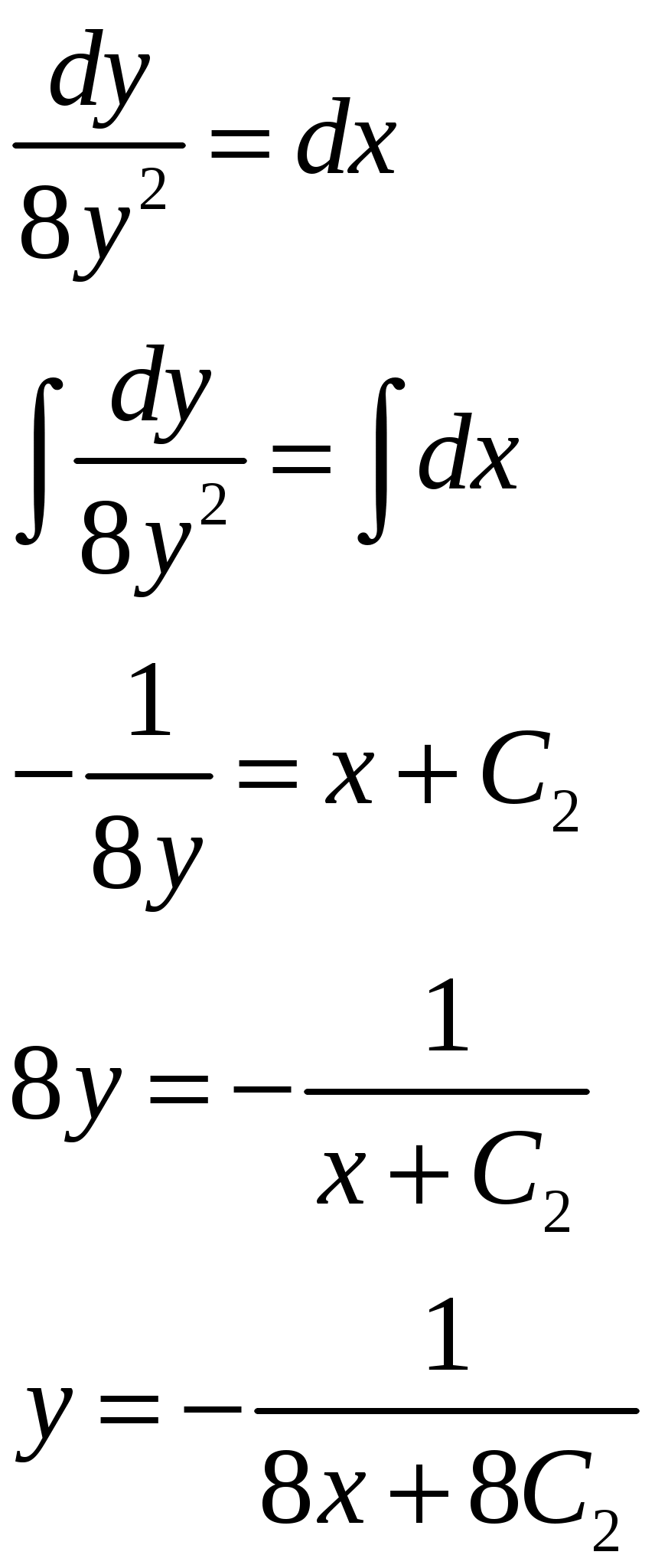, что больше нуля. Подставим начальные условия, чтобы найти константу: 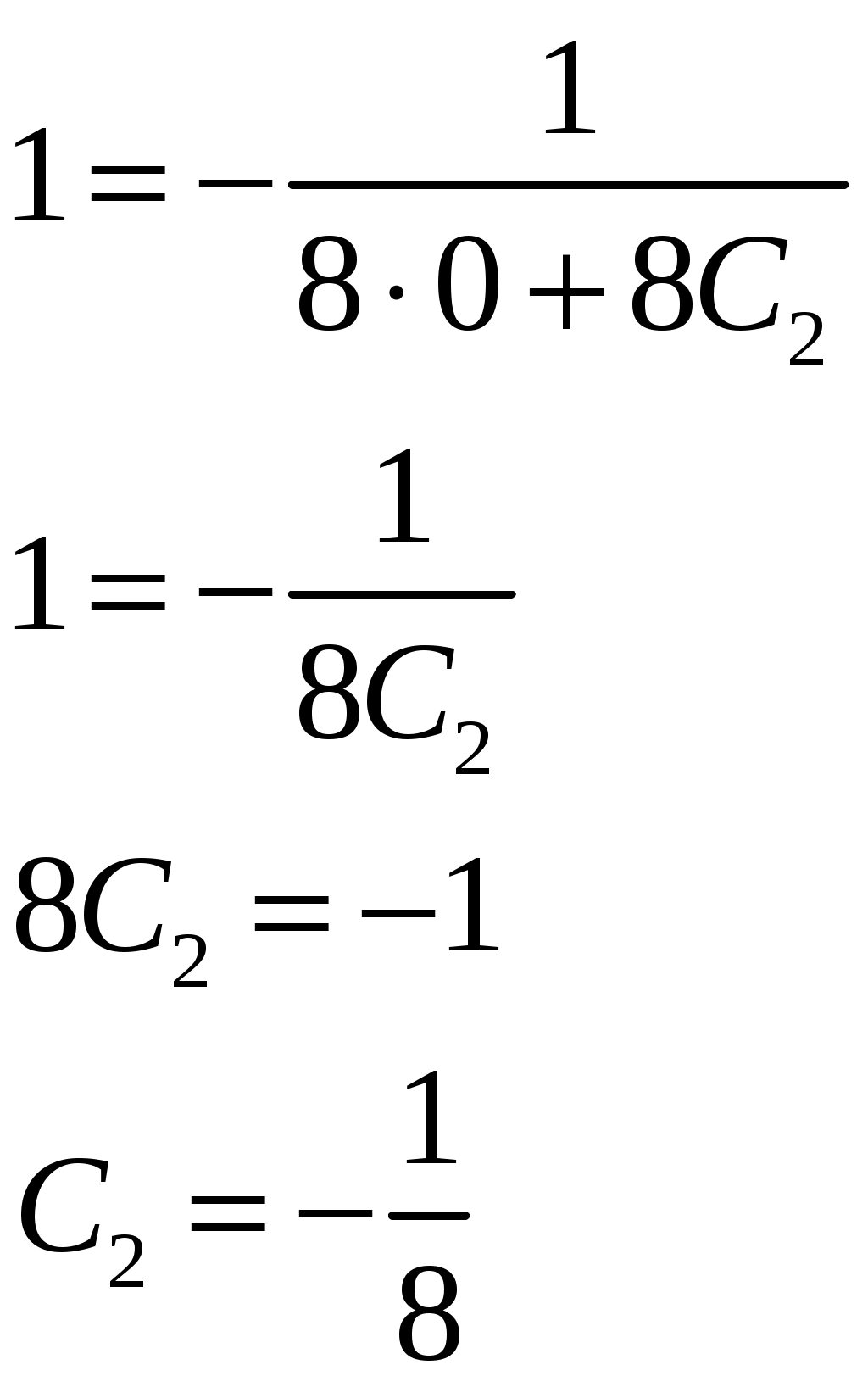 Следовательно, мы получаем, что  Найти общее решение дифференциального уравнения  Решение: Введем новую переменную  . Получим: Общее решение обыкновенного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами будет суммой общего решения соответствующего однородного уравнения и частного решения неоднородного. Сначала найдем общее решение соответствующего однородного уравнения  Сначала решим характеристическое уравнение: 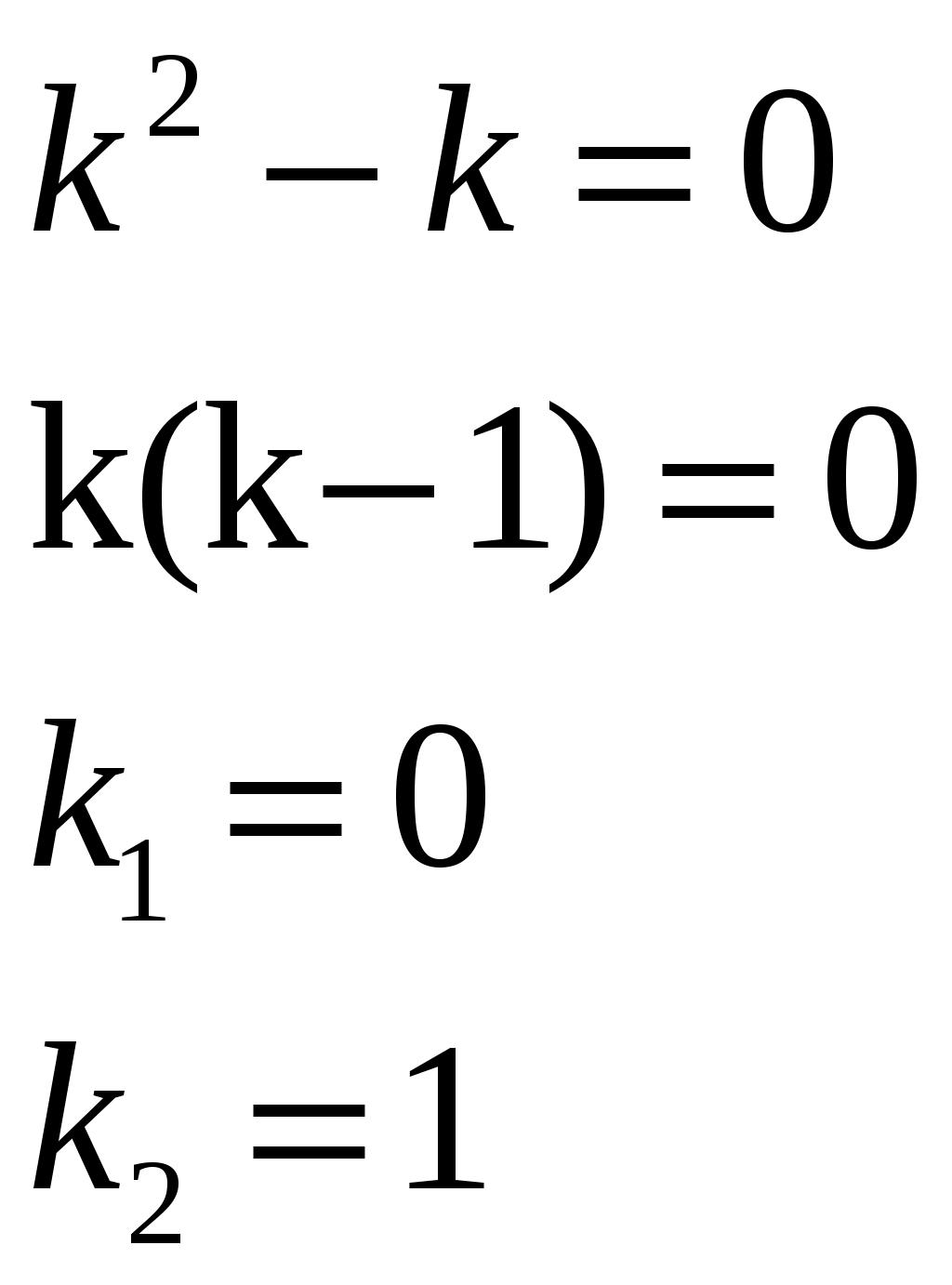 Корни нашего уравнения получились действительными и различными, следовательно, общее решение однородного уравнения можно записать в виде  Частное решение неоднородного уравнения подберем по виду правой части. Там у нас квадратный трехчлен, следовательно, будем искать частное решение в виде  Куб необходим, так как у нас нет члена без производных, следовательно, чтобы был квадрат в правой части необходим хотя бы куб. Найдем первую и вторую производную данного решения.   Подставим эти решения в наше исходное уравнение:  Откуда сразу видно, что  . Подставим это значение в исходное уравнение: Откуда сразу видно, что  . Подставим это значение в исходное уравнение: Откуда сразу видно, что  . Следовательно, частное решение имеет вид: А общее решение неоднородного уравнения имеет вид:  Вернемся к переменной 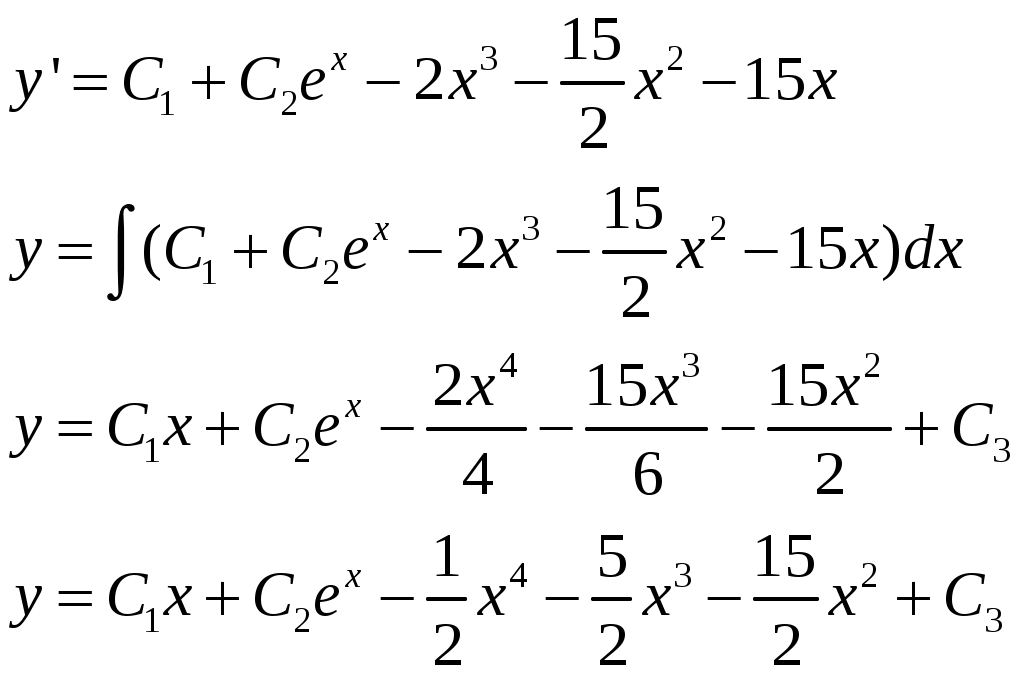: Найти общее решение дифференциального уравнения  Решение: Введем новую переменную . Получим: Общее решение обыкновенного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами будет суммой общего решения соответствующего однородного уравнения и частного решения неоднородного. Сначала найдем общее решение соответствующего однородного уравнения  Сначала решим характеристическое уравнение:  Корни нашего уравнения получились действительными и различными, следовательно, общее решение однородного уравнения можно записать в виде  Частное решение неоднородного уравнения подберем по виду правой части. Там у нас экспонента, умноженная на линейную функцию, однако экспонента в той же степени, что и в общем решении однородного уравнения, следовательно, будем искать частное решение в виде  Найдем первую и вторую производную данного решения.   Подставим эти решения в наше исходное уравнение:  Откуда сразу же получаем, что  , подставляем это в выражение для свободного члена, и получаем, что  .Следовательно, частное решение имеет вид:  А общее решение неоднородного уравнения имеет вид:  Вернемся к переменной 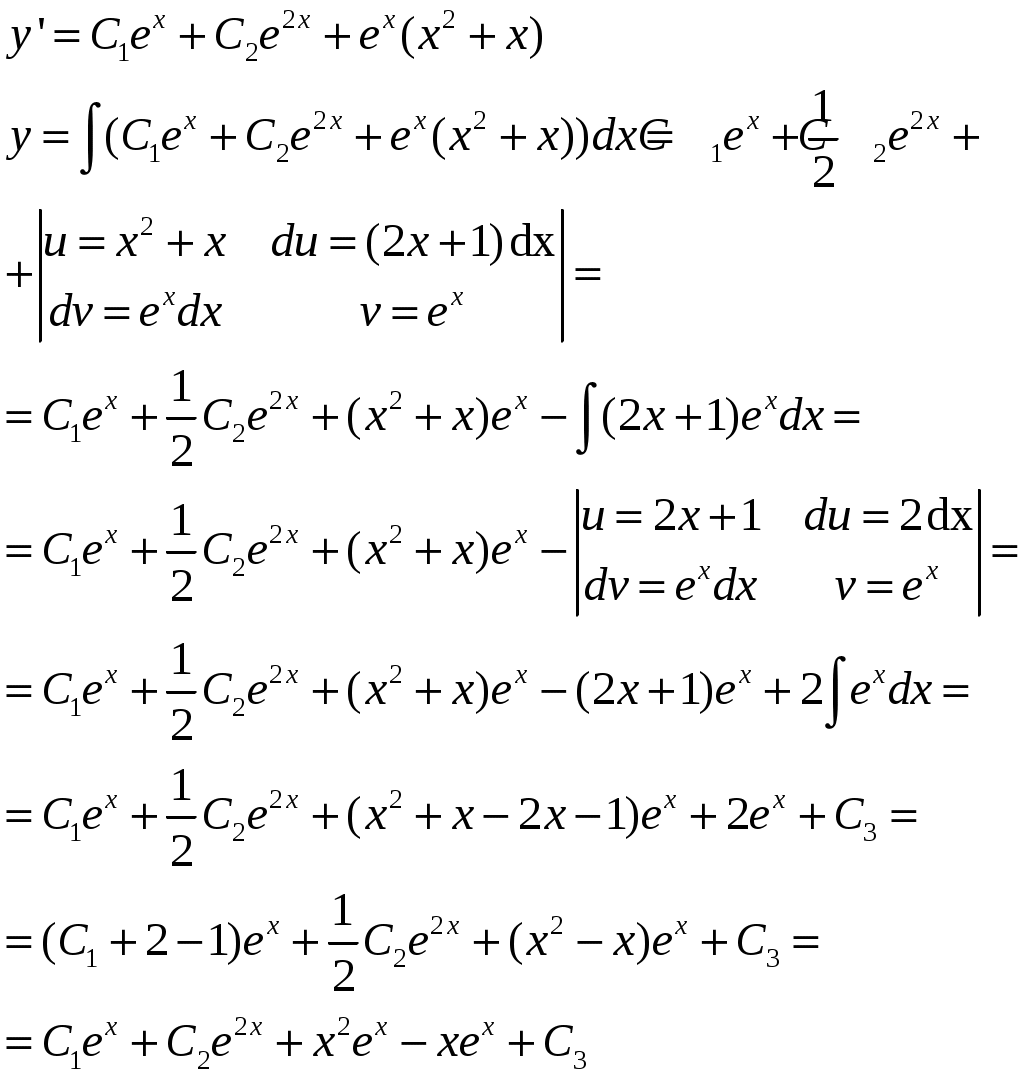: Мы учли, что  все равно остается константой, и  все равно остается константой.Найти общее решение дифференциального уравнения  Решение: Общее решение соответствующего обыкновенного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами будет суммой общего решения соответствующего однородного уравнения и частного решения неоднородного. Сначала найдем общее решение соответствующего однородного уравнения  Сначала решим характеристическое уравнение:  У нас получился один корень двойной кратности, следовательно, общее решение однородного уравнения можно записать в виде  Частное решение неоднородного уравнения подберем по виду правой части. Там у нас синус, умноженный на экспоненту, следовательно, будем искать частное решение в виде  Найдем первую и вторую производную данного решения.   Подставим эти решения в наше исходное уравнение: 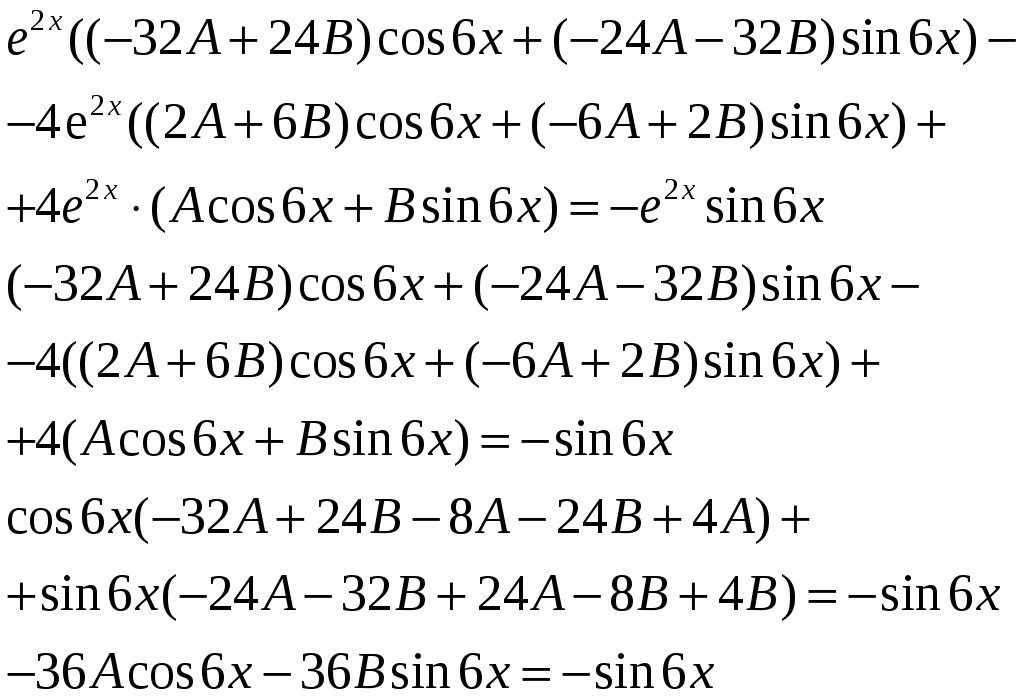 Откуда сразу видно, что  , а  .Следовательно, частное решение имеет вид:  А общее решение неоднородного уравнения имеет вид:  Найти общее решение дифференциального уравнения  Решение: Общее решение соответствующего обыкновенного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами будет суммой общего решения соответствующего однородного уравнения и частного решения неоднородного. Сначала найдем общее решение соответствующего однородного уравнения  Сначала решим характеристическое уравнение:  Наши корни комплексно сопряженные, следовательно, общее решение однородного уравнения можно записать в виде  Частное решение неоднородного уравнения подберем по виду правой части. Там у нас сумма синуса и косинуса, и экспоненты, следовательно, решение также будет суммой синуса, косинуса и экспоненты. Но так как аргумент синуса и косинуса совпадает с аргументом общего решения однородного уравнения, необходимо домножить их на  . То есть, будем искать частное решение в виде Найдем первую и вторую производную данного решения. 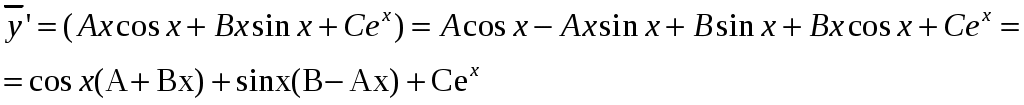 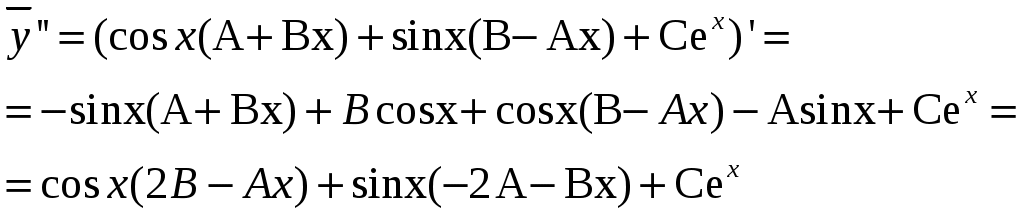 Подставим эти решения в наше исходное уравнение:  Откуда сразу видно, что  .Следовательно, частное решение имеет вид:  А общее решение неоднородного уравнения имеет вид:  Найти общее решение дифференциального уравнения  Решение: Введем новую переменную  . Получим: Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Общий вид таких уравнений следующий:  В нашем случае и  , и  .Решить такое уравнение можно домножив обе части уравнения на интегрирующий множитель, который можно найти по формуле: Если мы это сделаем, мы получим в левой части полный дифференциал: 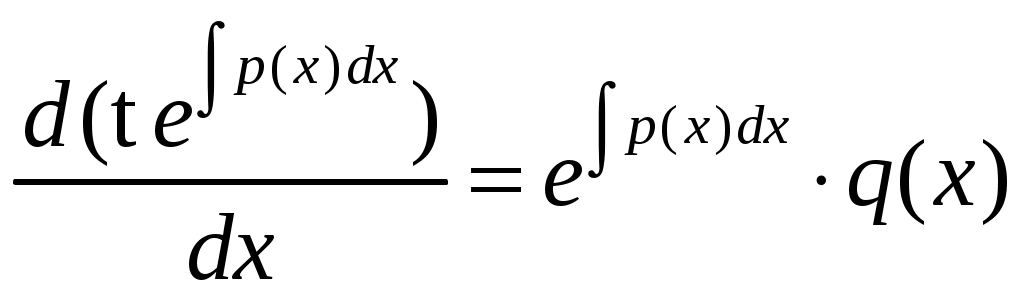  И получим уравнение с разделяющимися переменными. Найдем интеграл  В интегрирующем множителе нам не важна константа интегрирования. Найдем Q(x) для наших данных:  Домножим обе части уравнения на интегрирующий множитель: 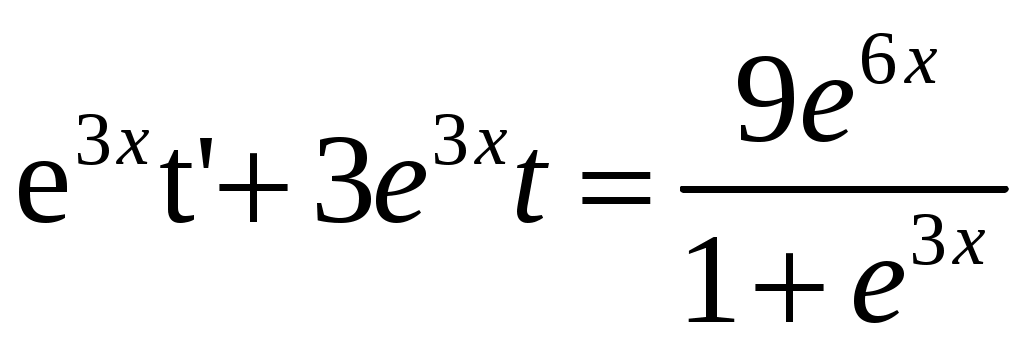 Левая часть получилась равна  . Проверим это: Следовательно, левую часть можно свернуть:  .Перенесем в правую часть уравнения: Проинтегрируем обе части:  Найдем правый интеграл отдельно. Получим:  Введем новую переменную 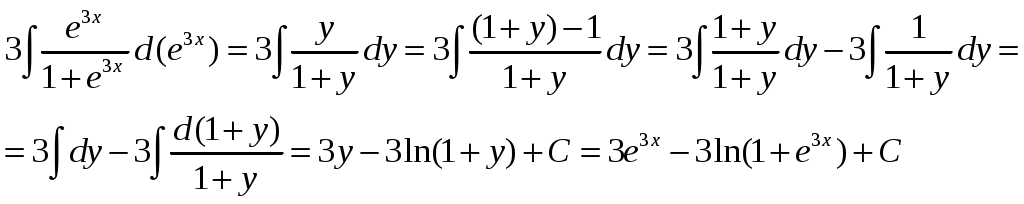 . Тогда Следовательно, получаем:  Вернемся к переменной : Чтобы найти второй интеграл, введем новую переменную  . Получим: Чтобы найти интеграл, воспользуемся методом неопределенных коэффициентов. Сложим две дроби:  Приравнивая коэффициенты при одинаковых степенях получаем, что 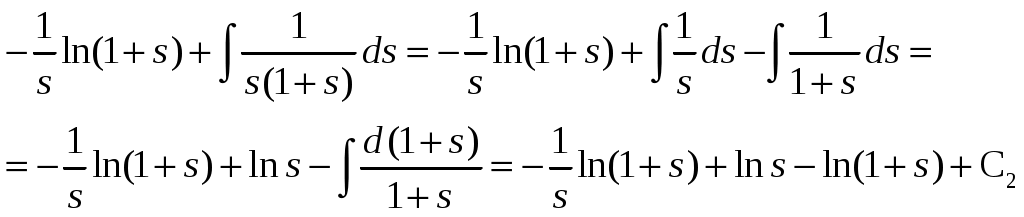 ,  . То есть, Вернемся к переменной 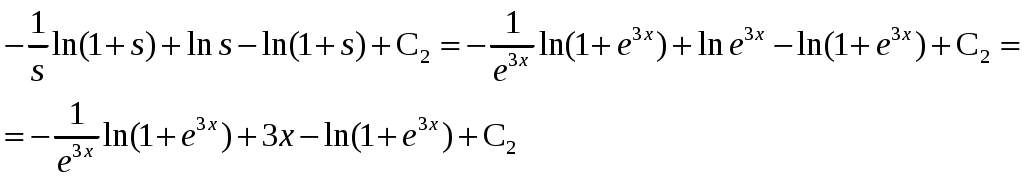: Теперь запишем общее решение: 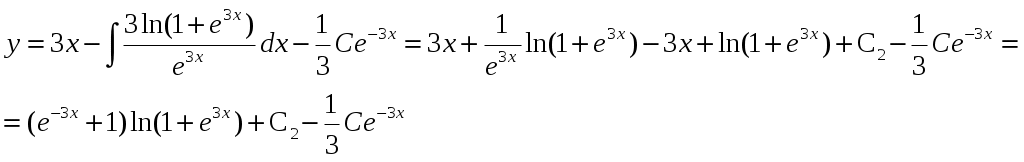 Решить систему дифференциальных уравнений методом Эйлера и операционным методом:  Решение: а) Метод Эйлера Метод Эйлера решения систем дифференциальных уравнений подходит только для решения однородных систем, то есть, таких систем, когда в них нет свободных членов или иных функций. В нашем же случае в первом уравнении системы есть свободный член «1». Следовательно, данную систему дифференциальных уравнений невозможно решить методом Эйлера. б) Операционный метод Преобразуем каждое из наших уравнений по таблице преобразований Лапласа. Будем использовать следующие преобразования:  Подставляем изображения в исходные уравнения: 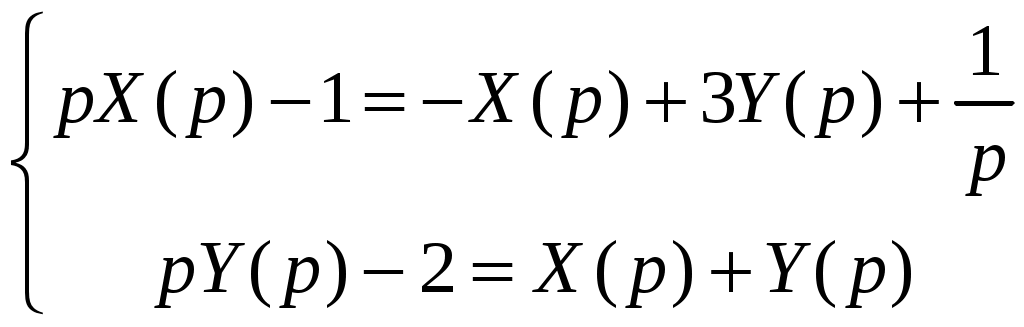 Перепишем нашу систему в виде 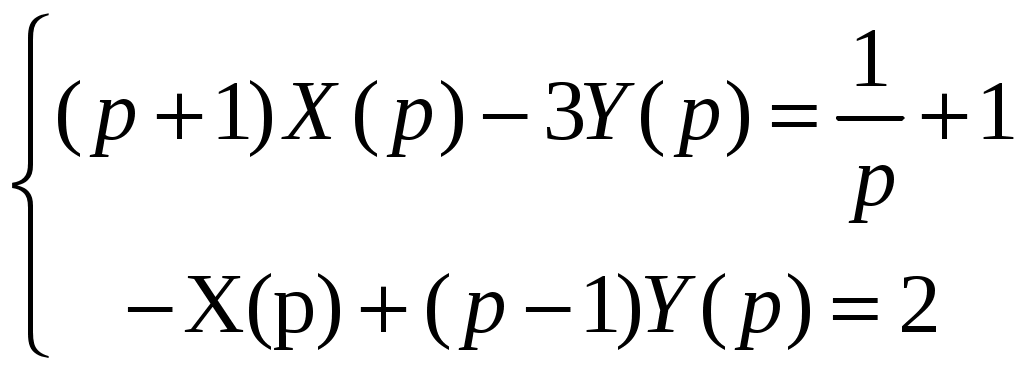 Полученную систему решаем по методу Крамера. Находим основной определитель системы: 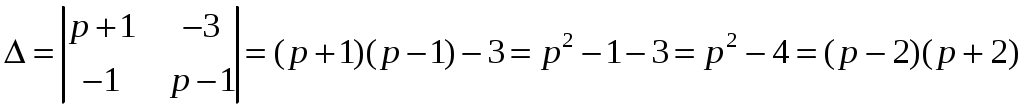 Находим корни:  Следовательно, корни нашего уравнения равны 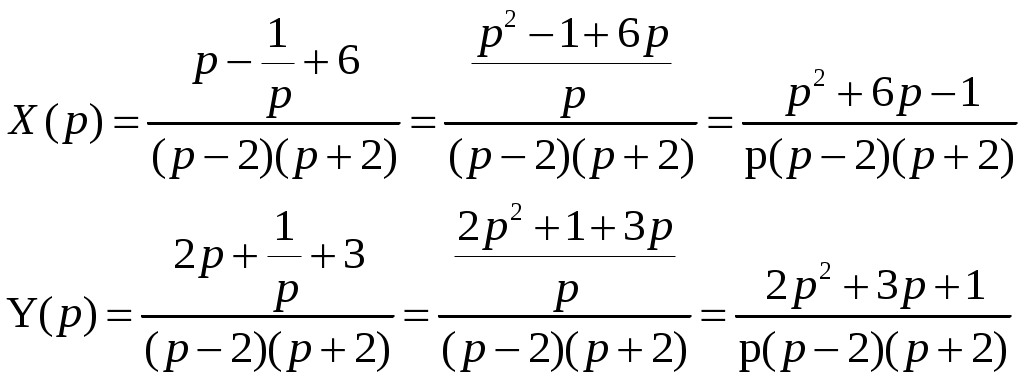 Далее нам необходимо разложить эти дроби на множители. Сначала разложим 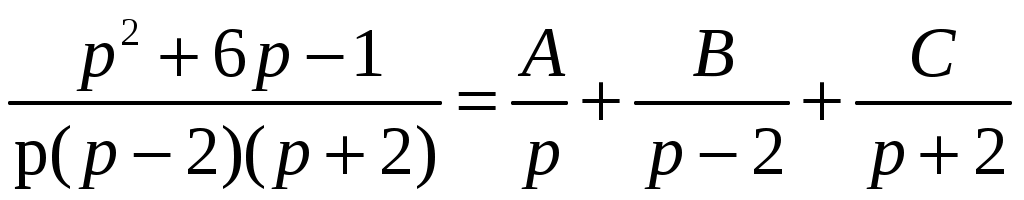 : Сложим эти дроби: 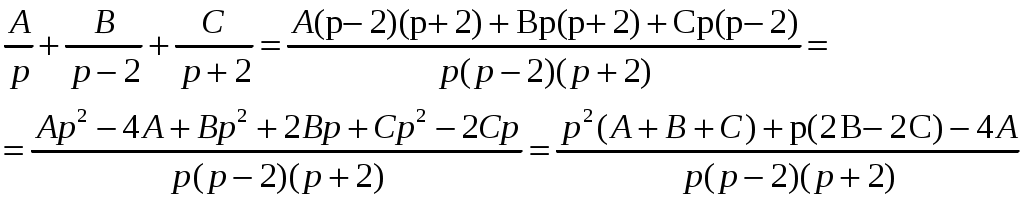 Приравняем коэффициенты при одинаковых степенях. Сразу же получаем, что  . Подставим это значение в нашу дробь: Получаем систему уравнений:  Или 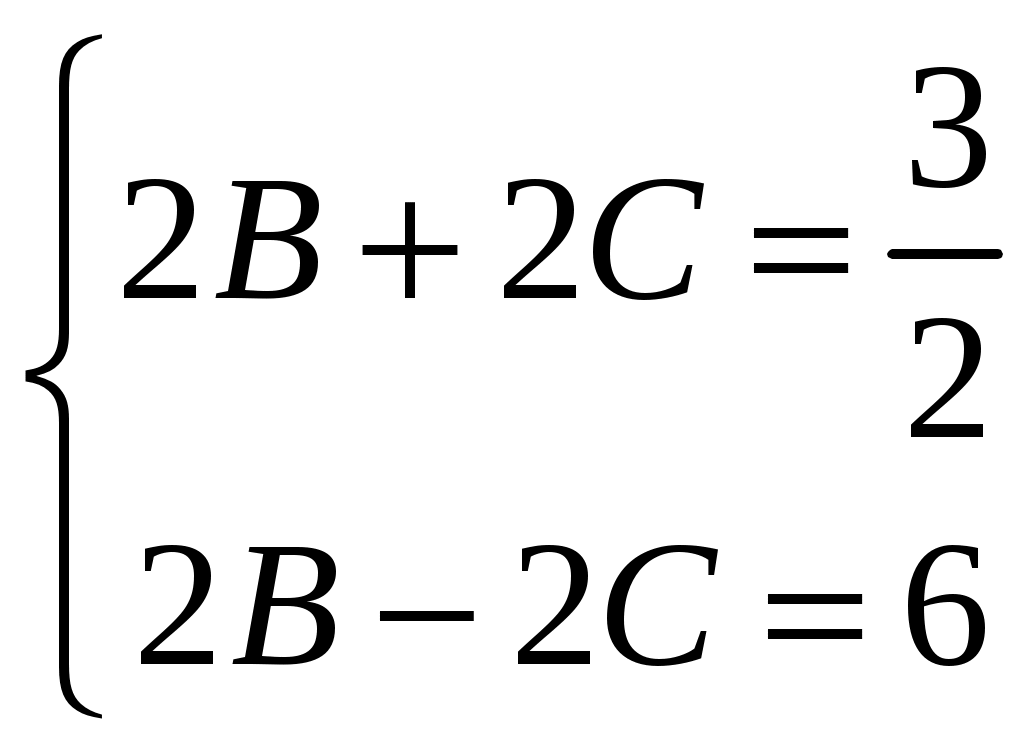 Сложим эти уравнения, получим, что  . Подставим это значение во второе уравнение, и получим, что  .Таким образом, 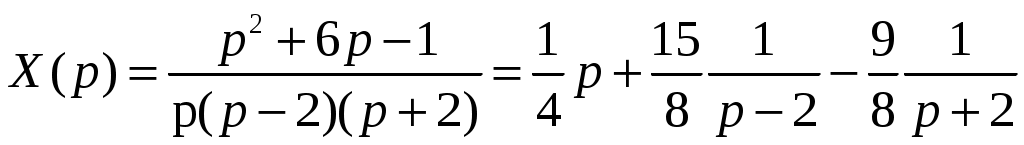 Выполним обратное преобразование Лапласа, и получим, что  Таким же образом разложим на дроби функцию 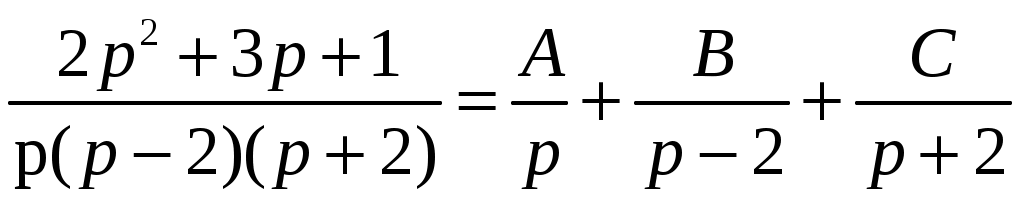 : Сложим эти дроби: 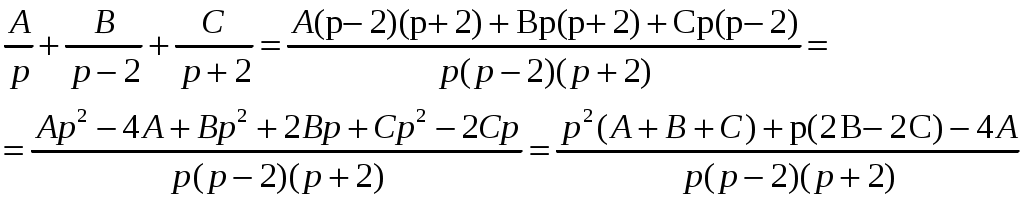Приравняем коэффициенты при одинаковых степенях. Сразу же получаем, что 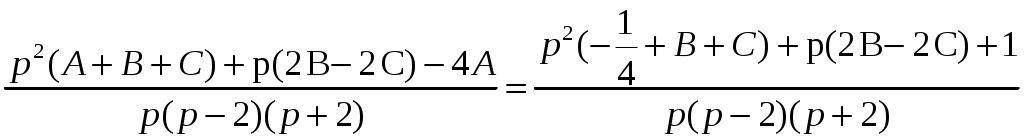 . Подставим это значение в нашу дробь: Получаем систему уравнений: 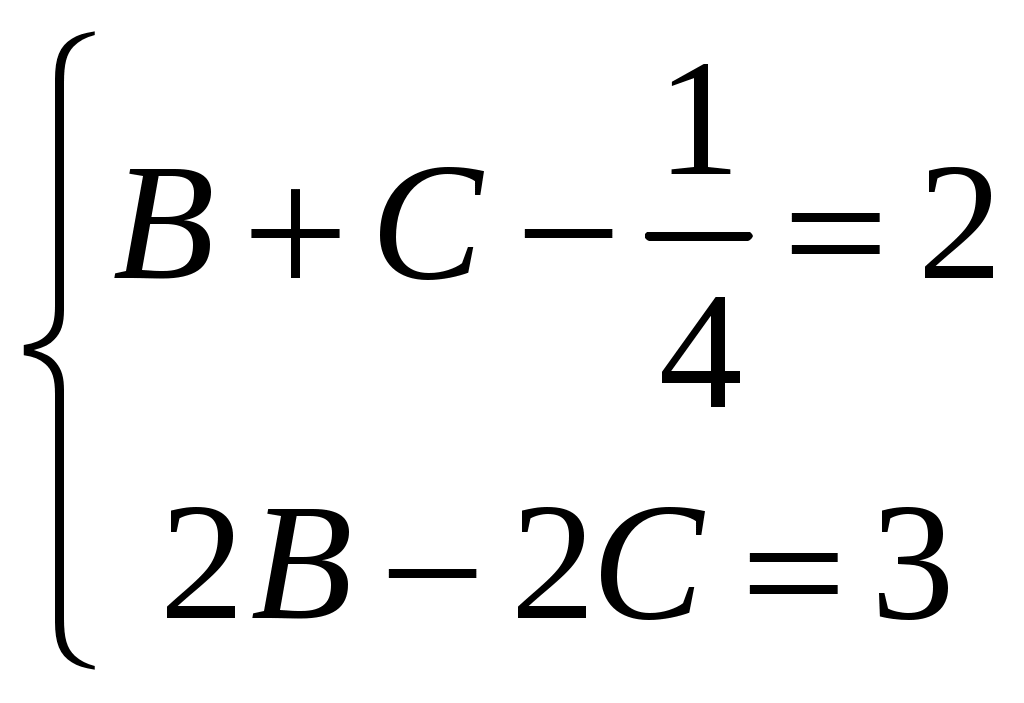 Или 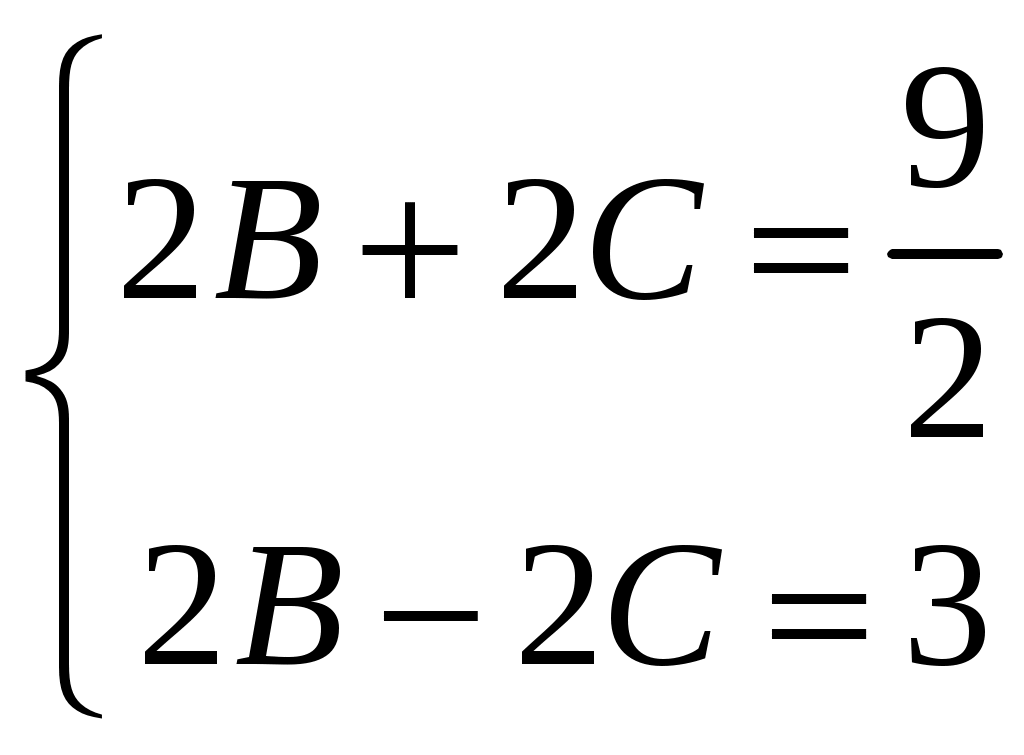 Сложим эти уравнения, получим, что . Подставим это значение во второе уравнение, и получим, что  .Таким образом, 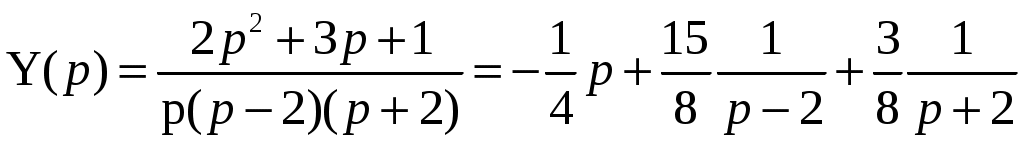 Выполним обратное преобразование Лапласа, и получим, что  Ответ: 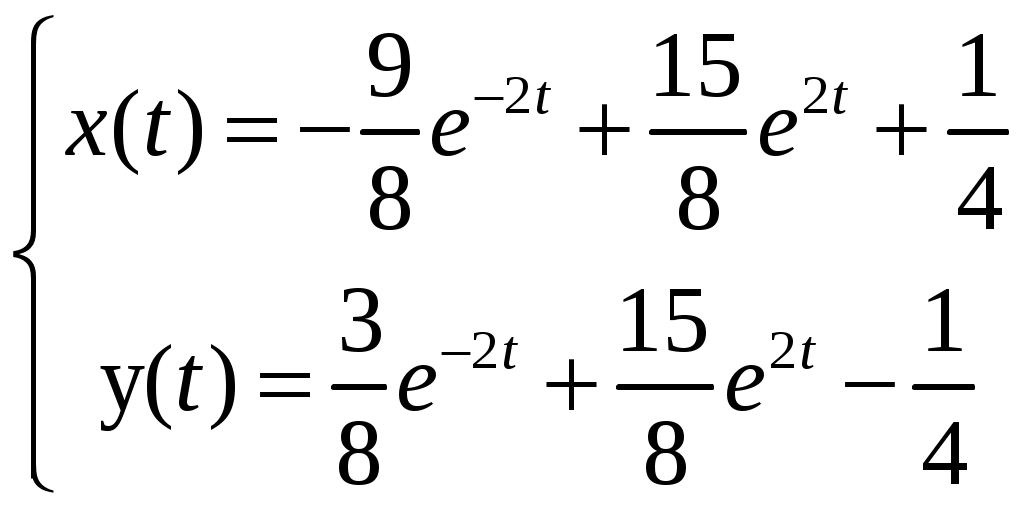 |