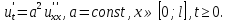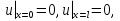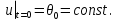Задача_8. Задача 8
 Скачать 319.27 Kb. Скачать 319.27 Kb.
|
 Задача 8
Решение: Для решения начально-краевой задачи (1) − (3) применим метод Фурье разделения переменных. Будем искать нетривиальное решение задачи в виде 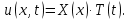 Подставим предполагаемую форму решения в исходное уравнение (1) 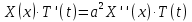 Разделим равенство на 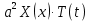 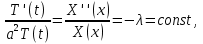 т.к. левая часть равенства зависит только от t, а правая – только от x. В результате переменные разделяются, и получается два линейных обыкновенных дифференциальных уравнения 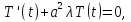 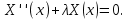 Подставляя 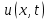 в виде в виде 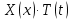 в граничные условия (2), получим в граничные условия (2), получим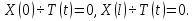 Поскольку равенства должны выполняться тождественно, то 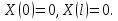 Таким образом, для функции 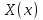 получили задачу Штурма-Лиувилля получили задачу Штурма-Лиувилля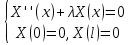 Общее решение уравнения имеет вид 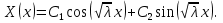 Неизвестные коэффициенты 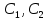 найдем из граничных условий найдем из граничных условий 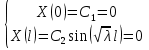 Получили спектральное уравнение для нахождения собственных значений 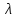 задачи Штурма-Лиувилля задачи Штурма-Лиувилля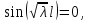 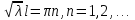 Собственные значения задачи равны 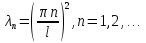 Им соответствуют собственные функции (с точностью до постоянного множителя) 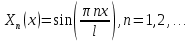 Уравнение для функции 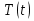 примет вид примет вид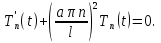 Общее решение этого уравнения имеет вид 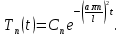 Решение 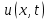 исходной задачи представим в виде ряда исходной задачи представим в виде ряда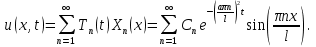 Коэффициенты 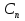 этого ряда найдем из начального условия (3) этого ряда найдем из начального условия (3)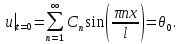 Коэффициенты 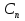 представляют собой коэффициенты разложения функции представляют собой коэффициенты разложения функции 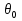 в ряд Фурье по собственным функциям в ряд Фурье по собственным функциям 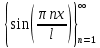 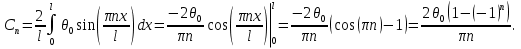 Таким образом, решение исходной начально-краевой задачи имеет вид 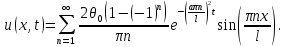 Учитывая, что 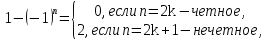 функцию 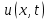 можно записать как можно записать как 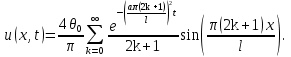 Ответ: 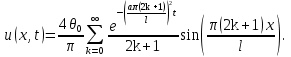 |