94,114 математика. Задание 94

• Название: Задание 94
• Дата: 12.07.2022
• Размер: 34.67 Kb.
• Имя файла: 94,114 математика.docx
• Тип: Решение; #629324

Содержание

Задание 94 3

Задание 114 3

Список использованных источников 6

Задание 94

Условие:

Вычислить несобственный интеграл или установить его расходимость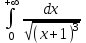


Решение:



Искомый интеграл сходится.

Задание 114

Условие:

Найти общее решение неоднородного линейного дифференциального уравнения.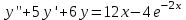


_{Решение:}

Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r² +5 r + 6 = 0

D=5² - 4·1·6=1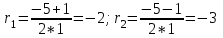



Корни характеристического уравнения:

r₁ = -2

r₂ = -3

Следовательно, фундаментальную систему решений составляют функции:

y₁ = e^-2x

y₂ = e^-3x

Общее решение однородного уравнения имеет вид: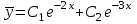

, C_i ∈ R

Рассмотрим правую часть:

f(x) = 12*x-4*e^-2*x

Поиск частного решения.

Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:

R(x) = e^αx(P(x)cos(βx) + Q(x)sin(βx)),

где P(x), Q(x) - некоторые полиномы
имеет частное решение

y(x) = x^ke^αx(R(x)cos(βx) + S(x)sin(βx))

где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).

Здесь P(x) = 12*x-4, Q(x) = 0, α = -2, β = 0.

Следовательно, число α + βi = -2 + 0i является корнем характеристического уравнения кратности k = 1(r₁).

Уравнение имеет частное решение вида:

y^· = x ((Ax + B)e^-2x)

Вычисляем производные:

y' = A*x*e^-2x-2*x(A*x+B)*e^-2x+(A*x+B)*e^-2x

y'' = 2(-4*A*x+A-2*B+2*x(A*x+B))*e^-2x

которые подставляем в исходное дифференциальное уравнение:

y'' + 5y' + 6y = (2(-4*A*x+A-2*B+2*x(A*x+B))*e^-2x) + 5(A*x*e^-2x-2*x(A*x+B)*e^-2x+(A*x+B)*e^-2x) + 6(x ((Ax + B)e^-2x)) = 12*x-4*e^-2·x

или

2*A*x*e^-2x+2*A*e^-2x+B*e^-2x = 12*x-4*e^-2·x

Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:

x: 2A = 0

1: 2A + B = -4

Решая ее, находим:

A = 0;B = -4;

Частное решение имеет вид:

y^·=x ((0x -4)e^-2x)=-4*x*e^-2·x

Таким образом, общее решение дифференциального уравнения имеет вид:

Список использованных источников

1. 
   Бугров, Я.С. Высшая математика в 3 т. Т.1 в 2 книгах. Дифференциальное и интегральное исчисление: Учебник для академического бакалавриата / Я.С. Бугров, С.М. Никольский. - Люберцы: Юрайт, 2016. - 501 c.
   
2. 
   Шипачев, В.С. Высшая математика. полный курс в 2 т. том 1: Учебник для академического бакалавриата / В.С. Шипачев. - Люберцы: Юрайт, 2016. - 288 c.