Дипломная работа по теме Элективный курс для 7-9 классов «Преобразование графиков функций». Дипломная работа. Элективный курс для 79 классов Преобразование графиков функций Содержание Введение
 Скачать 168.5 Kb. Скачать 168.5 Kb.
|
|
Дипломная работа по теме Элективный курс для 7-9 классов «Преобразование графиков функций» Содержание Введение ……………………………………………………………………….3 Глава 1. Способы преобразования графиков § 1. Анализ учебников, программ……………………………………………7 § 2. Осевая и центральная симметрия……………………………………….10 § 3. Параллельный перенос…………………………………………………..15 § 4. Сжатие и растяжение…………………………………………………….19 § 5. Графики функций, в формуле которых имеется знак модуля………...27 Глава 2. Элективный курс «Преобразование графиков функций» § 1. Требования к составлению программ…………………………………...29 § 2. Пояснительная записка к программе……………………………………31 § 3. Учебно-тематическое планирование……………………………………34 § 4. Дополнительный материал для проведения элективного курса…………35 Заключение…………………………………………………………………….47 Приложение……………………………………………………………………50 Введение В последние десятилетия функциональная линия школьного курса математики превратилась в одну из ведущих. Более того, её роль с течением времени постоянно возрастает. Работа посвящена вопросам использования графиков функций для решения различных задач. В ней подробно изложена тема преобразования графиков функций и разработан элективный курс по данной теме. Находясь на выставке картин, мы рассматриваем произведения искусств и обращаем внимание на то, сумел ли художник передать глубину, завершённость образного содержания. Картина является итогом длительных наблюдений и размышлений художника над жизнью. Представьте, что мы находимся на выставке картин, выполненных с помощью компьютера. В компьютерном «изобразительном искусстве» мы можем увидеть не что иное, как графики функций. Чтобы научиться видеть в таких картинах действительно графики функций, научиться создавать самим такие картины, необходимо знать основные функции и их свойства. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи, и порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В технике и физике часто пользуются графическим способом задания функций. Учёный – сейсмолог, анализируя сейсмограмму, узнаёт, когда было землетрясение, где оно произошло, определяет силу и характер толчков. Врач, исследующий больного, может по кардиограмме судить о нарушениях сердечной деятельности: изучение кардиограммы помогает правильно поставить диагноз заболевания. Инженер - радиоэлектронник по характеристике полупроводникового элемента выбирает наиболее подходящий режим его работы. Количество таких примеров легко увеличит. Более того по мере развития математики растёт проникновение графического метода в самые различные области жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике. Значит, растёт и важность изучения рассматриваемого раздела математики в школе, и особенно важность самостоятельной работы с ним. Существуют различные способы задания функций: - аналитический; - табличный; - словесный; - параметрический; - графический. Всегда, когда нужно выяснить общий характер поведения функций, обнаружить её особенности, график в силу своей наглядности является незаменимым. График функции есть изображение нашего понимания того, как ведёт себя функция. Для этого необходимо знать элементарные функции, их свойства и графики, владеть методами построения графиков. Предлагаемы элективный курс помогает вспомнить и подробнее изучить преобразования графиков функций. Элективный курс - обязательный для посещения курс по выбору учащихся, входящий в состав профиля обучения на старшей ступени школы. Реализация в предпрофильных классах элективных ориентационных курсов преследует своей целью подготовку учащегося к ситуациям выбора направления дальнейшего образования. Они могут рассматриваться и как инструмент внутрипрофильной дифференциации, и как средство компенсации профильной однонаправленности; как курсы, способствующие, расширению мировоззренческих представлений учащихся. Элективные курсы в 9 классе являются пропедевтическими и выполняют задачи практико-ориентированной помощи в приобретении личностного опыта выбора собственного содержания образования. В этой связи элективные курсы рассчитаны на небольшое количество часов, что позволяет школьникам в течение года попробовать себя в различных видах деятельности, в соответствии с профилями предлагаемыми конкретной школой, ресурсным центром, систеой муниципального и регионального образования. Курсы по выбору могут завершаться как экзаменационными испытаниями, так и защитой выполненного проектного или исследовательского задания. Реализация курсов по выбору в предпрофильной подготовке предполагает использование следующих потенциальных возможностей повышению готовности учащихся к самообразовательной деятельности: самостоятельное изучение основной и дополнительной учебной литературы, а также иных источников информации; сочетание обзорных и установочных лекций с лабораторными работами, семинарами, дискуссиями, творческими встречами; информационная поддержка образовательной деятельности учащегося с помощью учебных видеофильмов, электронных текстов, телекоммуникационных средств; проведение творческих конкурсов, публичных защит проектов, эвристических контрольных работ; включение в учебную деятельность экскурсий на выставки. Элективные курсы могут быть весьма разнообразными и выбираются исходя из конкретных условий (подготовка учителей, материально-техническая база, запросы учащихся и региональной специфики рынка труда и рынка образовательных услуг). Цель работы: - рассмотрение некоторых функций и их графиков; - рассмотрение основных методов построения графиков, опирающихся на простейшие приёмы. Объёкт исследовании: различные виды преобразования графиков функций. Предмет исследования: способы преобразования графиков функций, особенности построения элективного курса по данной теме. Задачи исследования: -познакомить с конкретными преобразованиями графиков функций; - показать применении данного материала в школе на элективном курсе; - формировать представление о математике как части общечеловеческой культуры. Гипотеза: целенаправленная работа при изучении темы будет способствовать в целом эффективности усвоения математических знаний, развитию логического мышления, нетрадиционных способов решения математических задач при следующих условиях: хорошего знания терминологии, умения строить простейшие графики, умения преобразовывать графики функций. В первой главе работы рассматриваются способы преобразования графиков, такие как: осевая и центральная симметрии, параллельный перенос, сжатие и растяжение, графики функций в которых имеется знак модуля. Материал данной главы является опорой при построении лекций и семинаров первых часов элективного курса. Во второй главе приведены требования к составлению программы элективного курса, сформулированы его цели и задачи, приведено учебно-тематическое планирование курса по выбору, рассмотрена структура программы, методы и формы обучения, даны примеры различных заданий , которые могут быть использованы при подготовке к занятиям. А также перечислены формы контроля, это написание рефератов, проведение творческих конкурсов. Для написания работы применялись следующие методы: - анализ научно-методической литературы; - обобщение опыта работы; Глава 2. Элективный курс «Преобразование графиков функций». § 1. Требования к составлению программ. К составлению программы элективного курса предъявляются следующие требования: 1. Степень новизны для учащихся. Программа включает материал, выходящих за рамки базовых программ. 2. Мотивирующий потенциал программы. Программа содержит знания, вызывающие основательный интерес учащихся. 3. Развивающий потенциал программы. Содержание программы способствует интеллектуальному, творческому, эмоциональному развитию школьников. 4. Здоровьесберегающие характеристики. Программа не создаёт учебных перегрузок школьников (отсутствие или необязательность домашних заданий), предполагает широкое использование активных методов и форм обучения. 5. Полнота содержания, программа содержит всё необходимое для достижения запланированных в ней целей. 6. Связность и систематичность изложенного материала. Содержание программы построено таким образом, что изучение всех последующих тем обеспечивается предыдущими или знаниями базовых образовательных предметов; прослеживаются связи между частными и общими знаниями. 7. Методы обучения. Программа преимущественно основывается на активных методах обучения (проектных, исследовательских, игровых и других). 8. Степень контролируемости. В программе конкретно определены ожидаемые результаты обучения и методы проверки их достижения. 9. Реалистичность с точки зрения ресурсов. Программа реалистична с точки зрения возможности использования учебно-методических и материально-технических средств, кадровых ресурсов школы. 10. Формальная структура программы. Наличие в программе необходимых разделов: пояснительной записки (с обязательным целеполаганием), основного (тематического) содержания, ожидаемых результатов обучения, списка литературы. § 2. Пояснительная записка к программе. В школе в большей мере осуществляется аналитический и формальный подход к изучению функций. Графикам же уделяется недостаточное внимание. В качестве упражнений на закрепление приводятся в основном функции, заданные аналитически, поэтому упускаются из вида несущественные их свойства. Ученики запоминают определения понятий, формулировки свойств формально, без подкрепления графическими примерами. В то время, как изучение поведения функций и построение их графиков часто помогает решать многие задачи, и порой является единственным средством их решения. Цели элективного курса: - обобщение знаний о функциях и их графиках; - рассмотрение основных методов построения, опирающихся на простейшие приёмы преобразования графиков; - развитие логического мышления; - создание ситуации погружения в «нетрадиционные» задачи; - формирование навыков анализа получаемой информации; - развитие интереса к математике. Задачи элективного курса: - научить строить более сложные графики функций, применяя элементарные преобразования; - овладеть конкретными преобразованиями графиков; - формировать представление о математике как части общечеловеческой культуры, понимания значимости математики; - удовлетворять потребности и запросы школьников, проявляющих интерес, склонности и способности к математике. Данный элективный курс разделён на две части: - теоретическая; - практическая. В первой части учащиеся приводят в систему все знания, которые у них имеются на момент начала курса по выбору. Знакомятся с основными преобразованиями графиков функций: осевая и центральная симметрия, параллельный перенос, равномерные осевые сжатия или растяжения, графиками функций в которых имеется знак модуля. Во второй части ребята учатся сами выполнять разные преобразования с графиками. В школе широко используются задания, в которых ученики строят точки по их координатам и последовательно соединяют их, получая при этом рисунок животного, птицы и другое. В предлагаемом курсе ученикам предлагается выполнять рисунки с помощью графиков функций и их преобразований. В дальнейшем будут приведены примеры таких рисунков. Они построены с помощью различных функций: квадратичной, линейной, кубической, функции у = х, у = х заданных на отрезке. Предлагаемые упражнения полезны для отработки навыков быстрого построения графика функции, повышения интереса к данной теме. Графики можно строить схематично, вычисляя значения функций на концах отрезка, используя преобразования известных графиков функций. При построении графиков квадратичных функций необходимо точно определить координаты вершины параболы и направления ветвей. В первой части курса применяются следующие методы и формы обучения: - формирование сознания (рассказ, объяснение, беседа, лекция, семинар); - стимулирования и мотивации деятельности (дискуссия, поощрение). Во второй части применимы такие методы, как: - организация деятельности и формирование опыта (упражнение, требование, инструктаж, иллюстрации, демонстрации, практические работы, проблемно-поисковые методы); - контроля эффективности (устный и письменный опрос, самопроверка, взаимопроверка, написание реферата, выполнение творческих работ). В конце изучаемого курса ребята выполняют на выбор одну из работ: написание реферата или выполнение рисунка с помощью различных графиков и их преобразований. На последних занятиях учащиеся защищают свои работы и получают зачёт. § 3. Учебно-тематический план.
§ 4. Дополнительный материал для проведения элективного курса. « О простых функциях и их графиках ». В данной теме ребята приводят в систему все знания, которые у них имеются. Ниже приведён план семинара по которому можно построить первое занятие. Также пункты плана используются как вопросы для подготовки к семинару. 1. Линейная функция. 2. Функция вида у = х . 3. Обратная пропорциональность у = 4. Функция у = х . 5. Квадратичная функция у = ах + вх + с. При подготовке к семинару ребят необходимо проинструктировать о том что должно содержаться в плане их ответа, а именно: - построение графической модели функции; - название графика; - область определения функции; - у наиб., у наим., у = 0, у > 0, у < 0; - непрерывность; - ограниченность; - выпуклость; - монотонность; - область значений функции. Весь материал учащиеся записывают в виде следующей таблицы представленной в приложении. Материал для подготовки лекций по темам: осевая и центральная симметрии, равномерные осевые сжатия или растяжения, графики функций в которых имеется знак модуля подробно изложен в первой главе работы. В первой главе можно взять материал и для подготовки к семинару по теме: Параллельный перенос . Изложим план семинара и тем по которым учащиеся готовят свои выступления. - параллельный перенос вдоль оси абсцисс; - параллельный перенос вдоль оси ординат; - параллельный перенос вдоль оси абсцисс и симметрия относительно прямой, параллельной оси ординат; - параллельный перенос вдоль оси ординат и симметрия относительно прямой, параллельной оси абсцисс. Приведём задания которые можно рассмотреть на практических и самостоятельных работах. Практическая работа №1. «О простых функциях и их графиках» Задание: Постройте графики данных функций. Укажите их свойства. у = 2х, у = 2х + 1, у = 2х – 5 у = х², у = (х – 2) ² + 4, у = - (х – 2) ² + 4 у = , у = --------, у = ------------ Практическая работа №2 «Осевая и центральная симметрии» Задание: Построить графики функций. Указать вид симметрии. у = - х и у = х у = х + 2 х – 1 и у = х – 2х – 1 у = - и у = у = - х + 2 х + 1 и у = х – 2 х – 1 у = - х и у = х² у = х² и у = -1 – х² у = 1 - и у = х – (1 – у)² = 0 и х – у² = 1 у = - х² - 2 х + 1 и у = х² - 2 х – 1 у² + х = 0 и у² - х = 0 Практическая работа №3. «Параллельный перенос» Задание: Построить графики функций. Указать вид преобразования. Можно ли выполнить данные построения с помощью другого преобразования. у = х² и у = (х – 2)² у = 2 – х и у = х и у = х – 2 у² - (х + 2) = о и у² - х = 0 х² + (у – 2)² = 1 и х² + у² = 1 4. Практическая работа №4 «Равномерные осевые сжатия или растяжения» Задание: Построить графики функций. Указать вид преобразования. Можно ли выполнить данные построения с помощью другого преобразования. у = 2х² и у = х² у = и у = х² + у² = 1 и 4 х² + у² = 1 2 у² - х = 0 и у² - х = 0 х² + у² = 1,5² и х² + 4 у² = 1,5² у = 2 х + 1 и у = х у = х² и у = (2х – 1 )² у = х² и у = -2 х² + 3 у = х² и у = (х + )² и у = 2 (х + )² у = 2 х² + 3 х + 1 5. Практическая работа №5 «Графики функций в которых имеется знак модуля» Задание: Построить графики функций. Перечислить виды преобразований, применяемые для построения. у = х² + 2 х – 1 и у = | х² + 2 х – 1 | у = х² - 2 х – 1 и у = | х |² - 2 | х | - 1 у = х² + 2 х – 1 и у = | х |² + 2| х | - 1 у = и у = | | у = | х | + 3 и у = | х + 3 | у = | х + 1| и у = | х – 1 | и у = | х + 1| + | х – 1| у = 2 х – 1 и у = |2 х - 1| 6. Практические работы № 6,7,8. «Нестандартные задачи на преобразование графиков» Задание 1: Постройте графики функций. Построение второго графика выполните на заданном промежутке. у = - 0,25 х², у = - 0,25 х² + 8, если х [ -2; 2 ] у = - 3 х , у = - 3 х + 1, если х [ -2; -1] у = - 3 х , у = - 3 х + 5 , если х [-5; -4] у = 0,5 х², у = 0,5 (х – 2)² - 5, если х [ 1; 3] Задание 2: 1) Постройте график у = -----------, используя график у = ----------. 2) Постройте график функции у = |х| - 1 , используя график у = |х|. Решение 2) График у = |х| - 1 сравним с графиком у = |х|. если точка х = |а| лежит на первом графике, то точка х = а, у = |а| - 1 будет лежать на втором графике. Поэтому каждая точка (а; |а| - 1) второго графика может быть получена из точки (а; |а| ) первого графика сдвигом вниз на 1 единицу, и весь график получается, если график у = |х| сдвинуть вниз на 1 единицу. (рис.23) 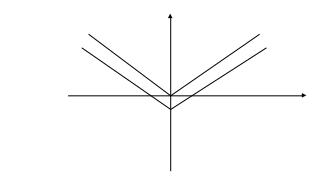 сдвиг сдвигвниз рис.23 Задание 3: Найти все линейные функции, которые при х = 3 принимают значения у = -5. Решение: Геометрически условие формулируется так: найти все прямые, проходящие через точку (3; -5). Любая (невертикальная) прямая, проходящая через начало координат, является графиком некоторой функции у = kx. Сдвинем эту прямую так, чтобы она проходила через нужную точку (3; -5), то есть на 3 единицы вправо и на 5 единиц вниз (рис ). После первого сдвига мы получим уравнение у = k ( x – 3), после второго у = k (х – 3) – 5. Ответ: Все линейные функции, которые при х = 3 принимают значения у = -5, выражаются формулой у = k (х – 3) – 5, где k – любое число. рис.24 Задание 4: Найдите наименьшее значение функции у = х² + 6 х +5. Решение: Наименьшее значение указанной функции – это ордината вершины параболы у = х² + 6 х +5. Чтобы определить координаты вершины, выделим полный квадрат: х² + 6 х +5 = (х + 3)² - 4. Теперь видно, что наша парабола получилась из у = х² сдвигом по оси Ох на 3 единицы влево и по оси Оу на 4 единицы вниз. Ответ: Наименьшее значение функции равно -4. Задание 5: Построить график у = -----------. Решение: Имеем ------------ = ------------- = --- (-----------) Ответ: График функции у = --------- - это график у = ----, сдвинутый по оси Ох на ( - ---) и сжатый по оси Оу втрое (рис. 25) рис. 25 Задание 6: На одном и том же чертеже построить графики трёх функций: 1) у = |х| 2) у = -|х| у = | х| + 2 у = - |х| +2 у= |х| - 3 у = - |х| - 3 Задание 7: На координатной плоскости задана симметрия относительно оси абсцисс. Найдите образы фигур, заданных уравнениями. у = х у = х+3 у = 4 х = -2 у = х² у = --- у = х х² + у² = 9 Задание 8: Построить график функции у = х |х|. Решение: Имеем ƒ (-х) =(- х) |-х| = - х |х| = - ƒ (х). Значит, функция нечётна, а поэтому график её симметричен относительно начала координат. Если х ≥ 0, то |х| = х, а ƒ (х) = х |х| = х х = х² . Значит, при х ≥ 0 имеем у = х². Графиком будет ветвь параболы. Она изображена на (рис.26). Подвергнув её преобразованию симметрии относительно начала координат, получим график функции у = х |х|. (рис.27) рис.26 рис.27 Практические работы № 9, 10, 11. «Графические фантазии». Задание 1: Кувшин №16. 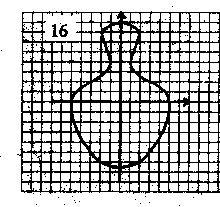 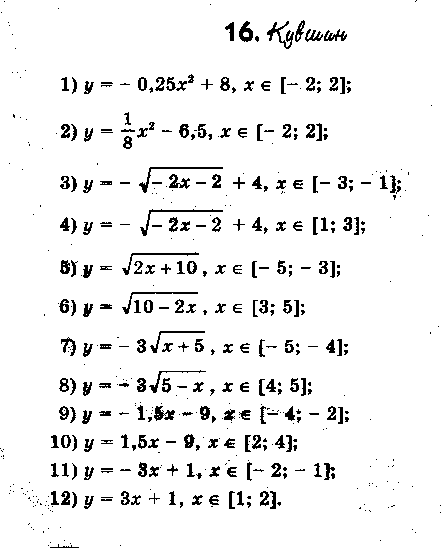 Задание 2. Верблюд № 6. 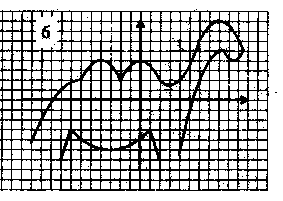 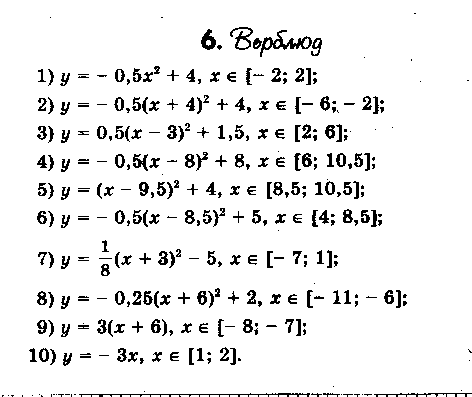 Задание 3. Парусник №1. 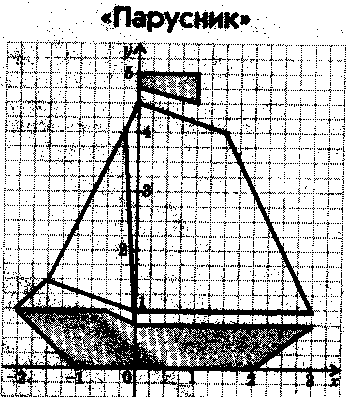 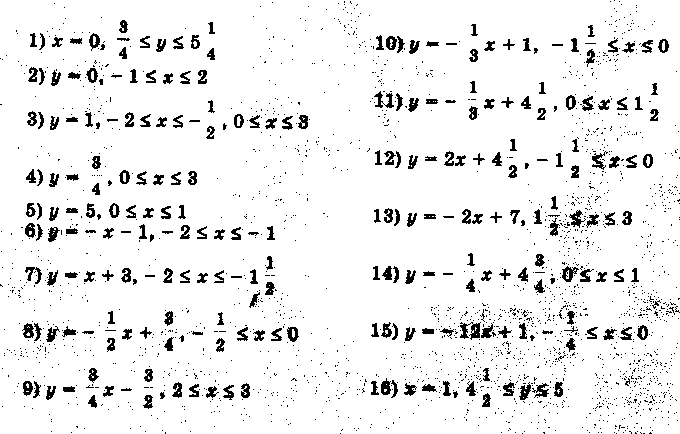 Задание №4 Очки №2 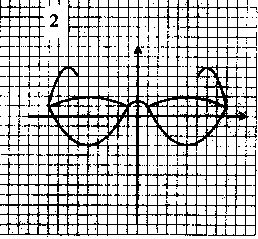 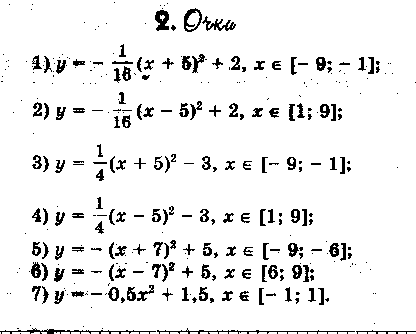 Задание № 5. Птица №4.  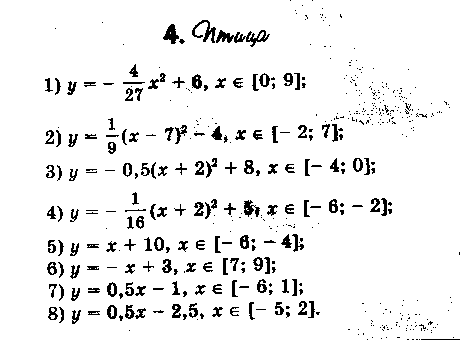 Задание №6. Сидящая кошка №10.  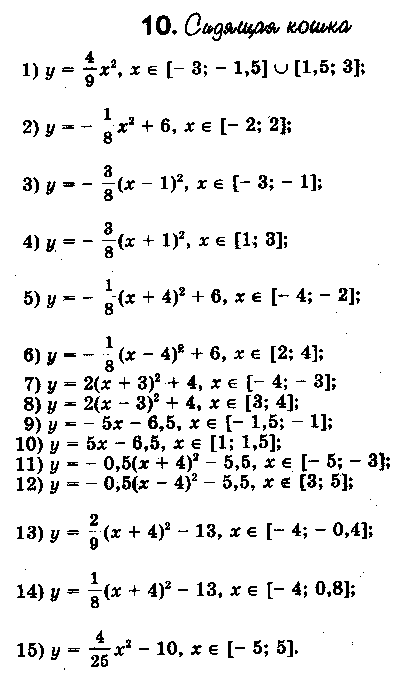 Задание №7. Самолёт 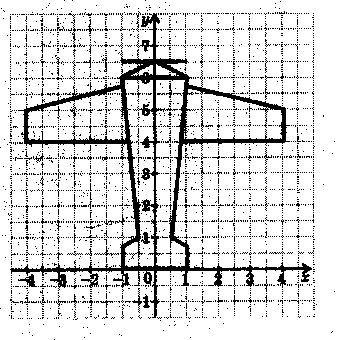 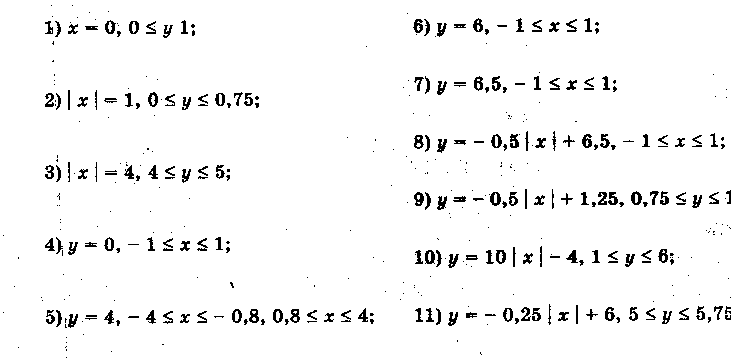 Задание №8. Шахматный король №9. 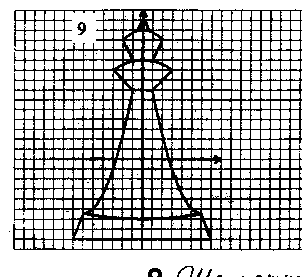 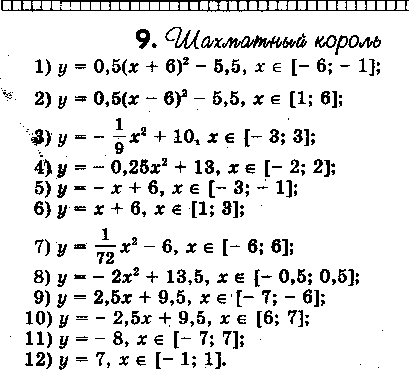 На самостоятельных работах ребята строят различные графики, используя преобразования, обсуждают решения. В теме «Графические фантазии» на самостоятельную деятельность выделено 2 часа. Данный материал помогает взглянуть на математику с другой стороны. В самостоятельных работах предлагается, чтобы учащиеся сами придумывали свои графики, рисунки и работали с ними. Здесь требуется внимание, фантазия для нахождения среди множества кривых того строительного материала, из которого могут получиться замечательные картинки. После проведения всех самостоятельных работ в кабинете можно организовать выставку получившихся рисунков. На последних четырёх занятиях ребята занимаются написанием рефератов или выполнением коллекции рисунков. Самостоятельное использование знаний представляет активный процесс, активную работу мысли, способствует получению глубоких и прочных знаний. Ниже приведены темы которые могут быть использованы для написания рефератов. Преобразования на примере линейной функции. Построение графиков функций путём сдвига графиков основных функций. Построение графиков квадратичных функций содержащих модуль. Преобразования на примере степенных функций. Преобразования на примере графика обратной пропорциональности. Зачет проводится в виде защиты рефератов или рисунков. |
