Ч.2. Электричество и магнетизм (1). Электри ество и магнетизм
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
Лабораторная работа № 4.1 МАГНИТНОЕ ПОЛЕ4.1.1. Цель работыЦелью лабораторной работы является знакомство с моделированием магнитного поля, создаваемого различными источниками, и экспериментальное определение величины магнитной постоянной. 4.1.2. Краткая теорияМагнитное поле (МП) создается проводниками с током, движущимися электрическими заряженными частицами и намагниченными телами. Силовой характеристикой МП служит вектор магнитной индукции B . Индукция МП численно равна магнитной силе, которая действует на единичный положительный точечный заряд, помещенный в данную точку пространства и движущийся с единичной скоростью перпендикулярно направлению МП. B FM . (4.1.1) qV МП может быть задано графически с помощью линий магнитной индукции. Линии магнитной индукции – линии, в любой точке которых вектор индукции МП направлен по касательной. Эти линии всегда замкнуты и никогда не пересекаются. Это является следствием отсутствия в природе магнитных зарядов. Для МП справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукции полей, создаваемых каждым током или движущимся зарядом в отдельности B Bi . (4.1.2) N i1 Индукция МП, создаваемого элементарным отрезком dl с током (элементом тока) в вакууме, определяется законом Био-Савара-Лапласа:
где 0 = 410–7 Гн/м – магнитная постоянная; – магнитная проницаемость окружающей среды. Магнитная проницаемость окружающей среды – скалярная безразмерная физическая величина, показывающая, во сколько раз индукция результирующего магнитного поля в веществе отличается от индукции магнитного поля в вакууме. Ввещ . (4.1.5) Ввак Закон Био-Савара-Лапласа и принцип суперпозиции позволяют получить для индукции МП прямого бесконечно длинного проводника с током формулу  0I , (4.1.6) 0I , (4.1.6) B 2r где r – кратчайшее расстояние от проводника с током до точки, в которой определяется индукция. Индукция МП создаваемого круговым витком радиуса R с током I в произвольной точке оси витка определяется по формуле:  02 pm , (4.1.7) 02 pm , (4.1.7) B 4(R2 r2)3/ 2 где pm ISn – магнитный момент витка площадью S; n – вектор нормали. Циркуляция вектора индукции МП, создаваемого в вакууме системой стационарных токов, равна произведению 0 на алгебраическую сумму токов, охватываемых контуром интегрирования. 0Ii . (4.1.8) l i Соленоидом называется длинная цилиндрическая катушка с током, состоящая из большого числа витков проволоки, расположенных вплотную друг к другу. Из теоремы о циркуляции можно получить формулу для индукции МП поля внутри бесконечно длинного соленоида B 0nI , (4.1.9) где n = N/l – число витков, приходящихся на единицу длины соленоида. Такое поле является однородным. Формула (4.1.9) справедлива также для соленоида конечных размеров, при выполнении условия l 10D, где l – длина соленоида, а D – его диаметр. 4.1.3. Порядок выполнения работыЗапустите программу «Открытая физика 1.1». Выберите раздел «Электричество и магнетизм». 1. Исследование магнитного поля прямого токаВыберите «Магнитное поле прямого тока». Нажмите вверху внутреннего окна на панели инструментов кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна. Рассмотрите внимательно рисунок 4.1.1. Найдите регулятор с движком, задающий силу тока и запишите его в таблицу «Регулируемые величины». в отчете (см. с. 6). 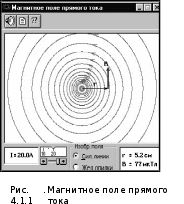 Зацепив мышью, перемещайте движок регулятора тока. Установите значение тока I1, указанное в таблице 4.1.1 для вашей бригады, и запишите его над табл. 4.1.2. Наблюдайте линии индукции МП прямого провода и зарисуйте их в отчет. Таблица 4.1.1 Значения величины тока
Удерживая нажатой левую кнопку мыши, перемещайте указатель мыши, который имеет форму руки, вблизи провода в горизонтальном направлении, останавливаясь на расстояниях r от оси провода, указанных в табл. 4.1.2. Значения индукции В1 в этих точках запишите в эту же таблицу. Повторите измерения для другого значения тока I2(см. табл. 4.1.1) и запишите В2 в табл. 4.1.2. Таблица 4.1.2 Результаты измерений I1 =______A, I2 =______A
2. Исследование магнитного поля витка с токомЗакройте окно эксперимента 1, нажав кнопку в правом верхнем углу внутреннего окна. Запустите, дважды щелкнув мышью, следующий эксперимент «Магнитное поле кругового витка с током» (рис. 4.1.2). Прочитайте краткие теоретические сведения. Зацепив мышью, перемещайте движок регулятора тока. Установите величину тока I1, указанную в таблице 4.1.1 для вашей бригады, и запишите над табл. 4.1.3. Наблюдайте линии индукции МП кругового витка (контура) и зарисуйте их в конспект. Удерживая нажатой левую кнопку мыши, перемещайте указатель мыши («руку») вдоль оси витка, останавливаясь на расстояниях r от его центра, указанных в таблице 4.1.2. В модели расстояние r обозначено как х. Значения индукции В1 в этих точках запишите в табл. 4.1.3. Повторите измерения для тока I2 (см. табл. 4.1.1) и запишите В2 в табл. 4.1.3. Значение радиуса витка R из окна эксперимента запишите над табл. 4.1.3. 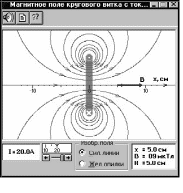 Рис. 4.1.2. Магнитное поле кругового витка с током Таблица 4.1.3 Результаты измерений I1 = ______ A, I2 =______A R =______см
3. Исследование магнитного поля соленоидаЗакройте окно эксперимента 2, нажав кнопку в правом верхнем углу внутреннего окна. Запустите, дважды щелкнув мышью, следующий эксперимент: «Магнитное поле соленоида» (рис. 4.1.3). Зацепив мышью, перемещайте движок регулятора тока. Установите величину тока I1, указанную в табл. 4.1.1 для вашей бригады. Наблюдайте линии индукции МП соленоида и зарисуйте их в конспект. Удерживая нажатой левую кнопку мыши, перемещайте указатель мыши («руку») по оси соленоида, останавливаясь на расстояниях х от центра соленоида, указанных в табл. 4.1.4. Значения индукции В1 в этих точках запишите в эту же таблицу. Повторите измерения для тока I2 (см. табл. 4.1.1) и запишите В2. Запишите над табл. 4.1.4 значения радиуса соленоида R и концентрации витков n. 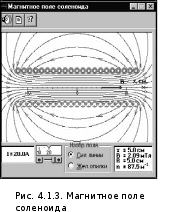 Таблица 4.1.4 Результаты измерений R = ______ см; n = ______ м-1
4.1.4. Обработка результатов измеренийВычислите и запишите в таблицы 4.1.2, 4.1.3 значения для второй строки. Постройте на одном листе графики зависимости индукции МП (B1 и В2) прямого провода с током от величины, обратной расстоянию (1/r). На линейной части графиков по тангенсу угла наклона (см. с. 7) рассчитайте два значения магнитной постоянной по формуле 0 2I  (1(B/ r)) . (4.1.10) (1(B/ r)) . (4.1.10) Постройте на втором листе графики зависимости индукции МП (B1 и В2) на оси витка с током от величины [1/(R2+r2)3/2]. По тангенсу угла наклона графиков (см. с. 7) рассчитайте два значения магнитной постоянной по формуле  0 2IS1/(R2 (Br) 2 )3/ 2 , (4.1.11) 0 2IS1/(R2 (Br) 2 )3/ 2 , (4.1.11) где S = R2 – площадь витка. Вычислите для каждого эксперимента среднее значение магнитной постоянной и сравните с табличным значением, равным 410–7 Гн/м. Рассчитайте среднюю абсолютную и относительную погрешности для обоих экспериментов и запишите ответы (см. с. 7–8). На третьем листе постройте графики зависимости индукции МП (B1 и В2) на оси соленоида от расстояния х до его центра. Для магнитного поля соленоида при каждом токе определите протяженность r области однородности, в которой индукция меняется не более, чем на 10 % от максимальной Вmax. Для этого вычислите 0,9Вmax и определите, какому интервалу значений х оно соответствует. Это и будет r. КОНТРОЛЬНЫЕ ВОПРОСЫ1. Назовите источники МП. 2. Что называется индукцией МП? Как определяется направление вектора B в данной точке пространства? Сформулируйте принцип суперпозиции для вектора индукции. Запишите закон Био-Савара-Лапласа. Запишите и поясните теорему о циркуляции индукции МП. Запишите формулу для индукции МП прямого бесконечно длинного проводника с током. Как выглядят линии МП прямого проводника с током? Запишите формулу для индукции МП на оси кругового витка с током. Как направлен вектор индукции в центре витка с током? Что такое соленоид и чему равна индукция МП внутри бесконечно длинного соленоида? Является ли МП внутри соленоида однородным? |

 dB 02[I dl r],
dB 02[I dl r],