Ч.2. Электричество и магнетизм (1). Электри ество и магнетизм

• Название: Электри ество и магнетизм
• Дата: 26.03.2022
• Размер: 1.23 Mb.
• Имя файла: Ч.2. Электричество и магнетизм (1).docx
• Тип: Руководство; #417361
• страница: 13 из 15

Лабораторная работа № 4.4 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В RLC-КОНТУРЕ

4.4.1. Цель работы

Целью лабораторной работы является экспериментальное подтверждение закономерностей при вынужденных колебаниях в RLC-контуре.

4.4.2. Краткая теория

Колебание – любой физический процесс, характеризующийся той или иной повторяемостью в пространстве и времени.

Для того, чтобы в реальном колебательном контуре колебания продолжались длительное время, необходимо восполнять потери энергии. Для этого в цепь колебательного контура необходимо добавить дополнительный источник энергии: генератор с ЭДС, изменяющейся по гармоническому закону. В этом случае колебания будут не свободными, а вынужденными.

Вынужденными колебаниями называются процессы, происходящие в контуре, содержащем конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС, которые включены последовательно и образуют замкнутую электрическую цепь (рис. 4.4.1).

_I R

L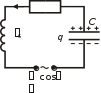

0 t

Рис. 4.4.1. Колебательный контур, в котором возникают вынужденные колебания

Для того, чтобы определить закон, по которому с течением времени изменяется заряд конденсатора, используем второе правило Кирхгоффа:

UС+UR= S + (t) = S + 0 cos ωt , где UC  q – напряжение на конденсаторе; C UR = IR – напряжение на резисторе; S  L dI – ЭДС самоиндукции в катушке; dt (t) = 0 cos ωt – переменная ЭДС источника тока. Сила тока в цепи (по определению)		(4.4.1)
I  dq .		(4.4.2)

dt

Подставив записанные выше выражения в формулу (4.4.1) с учетом (4.4.2), получим дифференциальное уравнение для заряда конденсатора в случае вынужденных колебаний:

^ddt^22q  2 ^dqdt ₀²_q ^L⁰ cost , (4.4.3)

где ₀ ^{ 1} – собственная частота колебательного контура; LC

^{ R} – коэффициент затухания.

2L

В установившемся режиме (через t = 5τ, где τ – время, в течение которого амплитуда затухающих колебаний уменьшается в е = 2,72 раза) заряд конденсатора

q t( ) q_mcos(t ), (4.4.4)

где q_m – амплитуда колебаний заряда конденсатора;  – начальная фаза вынужденных колебаний.

Сила тока в цепи при установившихся вынужденных колебаниях в контуре

I(t) = I_m sin (ωt + Ψ), (4.4.5)

где I_m – амплитуда тока.

Напряжение на конденсаторе в цепи колебательного контура

U_С(t) = U_Сmcos (ωt + Ψ), (4.4.6)

где U_Сm– амплитуда колебаний напряжения на конденсаторе.

В RLC-контуре при вынужденных колебаниях возможны резонанс тока и резонанс напряжения.

Амплитуда колебаний напряжения на конденсаторе U_Сm существенно зависит от частоты ω. При некотором значении этой частоты значение U_Сm достигает максимального. Это явление называется резонансом напряжения, а соответствующая частота – резонансной частотой ^U_рез.

^U_рез  ₀² 2² . (4.4.7)

Амплитуда напряжения на конденсаторе при резонансе пропорциональна амплитуде ЭДС и добротности контура Q,т. е.

U_0C = Q₀ . (4.4.8)

Отсюда можно оценить добротность контура, которая определяет, во сколько раз амплитуда колебаний напряжения на конденсаторе при резонансе больше амплитуды колебаний ЭДС генератора.

Q  ^U0C . (4.4.9)