Ч.2. Электричество и магнетизм (1). Электри ество и магнетизм

• Название: Электри ество и магнетизм
• Дата: 26.03.2022
• Размер: 1.23 Mb.
• Имя файла: Ч.2. Электричество и магнетизм (1).docx
• Тип: Руководство; #417361
• страница: 12 из 15

Лабораторная работа № 4.3 СВОБОДНЫЕ КОЛЕБАНИЯ В RLC-КОНТУРЕ

4.3.1. Цель работы

Целью лабораторной работы является экспериментальное исследование закономерностей свободных затухающих колебаний и определение величины индуктивности контура.

4.3.2. Краткая теория

Колебания – любой физический процесс, характеризующийся той или иной повторяемостью в пространстве и времени.

При гармонических колебаниях колеблющаяся физическая величина изменяется с течением времени по закону синуса или косинуса.

Свободные колебания – это колебания, происходящие за счет энергии, запасенной первоначально в системе. В процессе свободных колебаний восполнения потерь энергии не происходит. Свободные электромагнитные колебания возникают в колебательном контуре.

Колебательным контуром называется замкнутая электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью С, катушки с индуктивностью L и электрического сопротивления R (рис. 4.3.1).

R

L

Рис. 4.3.1. Реальный колебательный контур

Если сопротивление R =0, то электромагнитные колебания в контуре являются незатухающими из-за отсутствия потерь энергии, а колебательный контур – идеальным.

В идеальном колебательном контуре возможны гармонические незатухающие колебания тока I, заряда конденсатора q и напряжения на конденсаторе U_C.

По второму правилу Кирхгофа для идеального колебательного контура можно записать

UC S , где UC  q  напряжение на конденсаторе; C S  L dI  ЭДС самоиндукции в катушке. dt Сила тока в цепи (по определению)		(4.3.1)
I  dq .		(4.3.2)

dt

Подставив записанные выше выражения в формулу (4.3.1) с учетом (4.3.2), получим дифференциальное уравнение незатухающих колебаний для заряда конденсатора.

^d2q ₀²q  0, (4.3.3)

₂

dt

где ₀ ^{ 1}  собственная частота свободных колебаний в контуре. LC

Решая это дифференциальное уравнение, можно получить, что заряд конденсатора с течением времени изменяется по гармоническому закону:

q t( ) q₀ cos(₀t ₀), (4.3.4)

где q₀ – амплитуда колебаний заряда; ₀ – начальная фаза колебаний.

Период электромагнитных колебаний определяется по формуле Томсона:

T  ^2 2 LC . (4.3.5)

₀

Если в колебательном контуре присутствует активное сопротивление R, то свободные колебания в контуре будут затухать из-за потерь энергии: нагрев проводников, гистерезис в сердечнике катушки индуктивности, поляризация диэлектрика внутри конденсатора.

Согласно II правилу Кирхгофа (см. рис. 4.3.1)

U_C U_R _S , (4.3.6)

где U_R  IR – напряжение на резисторе.

Дифференциальное уравнение свободных затухающих колебаний имеет вид

^{d 22q}  2 ^dqdt ₀²q  0, (4.3.7) dt

где ^{ R}  коэффициент затухания свободных колебаний в контуре. 2L

Колебания возникают в контуре, если его сопротивление R меньше критического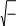

R_к 2 ^L . (4.3.8)

C

Решая дифференциальное уравнение (4.3.7) при R < R_к, можно получить, что заряд конденсатора в случае свободных затухающих колебаний изменяется по закону

q t( )q e^t cos(t ), (4.3.9)

m0

где q  заряд конденсатора в начальный момент времени; m0

q _e^t  амплитуда колебаний заряда конденсатора; m0

 _^ ^  частота затухающих колебаний.

На рис. 4.3.2. приведен график зависимости амплитуды затухающих колебаний от времени.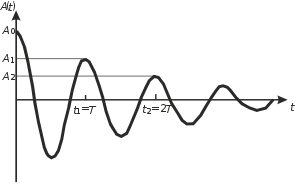



Рис. 4.3.2. Зависимость амплитуды затухающих колебаний от времени

Время затухания колебаний в контуре   это время, за которое амплитуда колебаний уменьшается в е = 2,72 раз.

Логарифмическим декрементом затухания  называется величина, определяемая натуральным логарифмом отношения амплитуды колебаний в данный момент времени t к амплитуде колебаний через время, равное периоду колебаний

ln ^{A( )t} . (4.3.10)

A(t T)

Для затухающих электромагнитных колебаний, с учетом (4.3.9)

 T . (4.3.11)

Добротность контура Q – это величина, обратно пропорциональная логарифмическому декременту затухания



Q  . (4.3.10)



Чем больше добротность контура, тем медленнее затухают колебания.

4.3.3. Порядок выполнения работы

Запустите программу «Открытая физика 1.1». Выберите раздел «Электричество и магнетизм» и «Свободные колебания в RLC-контуре». Нажмите вверху внутреннего окна на панели инструментов кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

Внимательно рассмотрите рис. 4.3.3, найдите регуляторы с движками, задающими индуктивность контура L, электроемкость конденсатора С и сопротивление R, и запишите их в таблицу «Регулируемые величины» в отчете

(см. с. 6).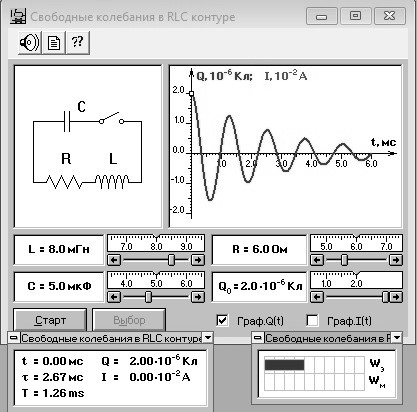



Рис. 4.3.3. Свободные колебания в RLC- контуре

Нажмите мышью кнопку «Выбор». Подведите маркер мыши к движку регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину емкости конденсатора и установите числовое значение, указанное в табл. 4.3.1 для вашей бригады. Аналогичным способом установите величину индуктивности в соответствии с табл. 4.3.1. Запишите установленные значения над табл. 4.3.2.

Установите сопротивление резистора R = 1 Ом. Нажав кнопку «Старт», наблюдайте за движением маленького квадратика по графику зависимости заряда конденсатора от времени.

Измерьте в пошаговом режиме семь значений амплитуд колебаний заряда конденсатора(Q₀, Q₁ – Q₆).

В начальный момент времени t = 0 первое значение амплитуды Q₀ = 210^–6 Кл. Это нулевой максимум.

Щелкните мышью кнопку « », расположенную на панели инструментов в верхней части окна программы, затем «Старт». После этого нажимайте мышью несколько раз кнопку «» вверху окна, пока метка (маленький квадратик) на графике q(t) не окажется на вершине первого максимума. Запишите с экрана значение амплитуды Q₁ в табл. 4.3.2.

Опять нажимайте мышью несколько раз кнопку «», пока метка не окажется на вершине второго максимума, и запишите Q₂. Далее аналогично измерьте значения остальных амплитуд колебаний заряда.

Запишите из окна модели значение времени затухания  в табл. 3.4.2

Меняя сопротивление R, повторите измерения амплитуд и заполните таблицу 4.3.2.

Таблица 4.3.1

Значения емкости конденсатора и индуктивности катушки

Номер бригады	1	2	3	4	5	6	7	8
С, мкФ	3	3	2,7	2,7	2,4	2,4	2	2
L, мГн	6	7	8	9	10	9	8	7

Таблица 4.3.2

Результаты измерений

С = ____ мкФ, L = ____ мГн, Т = ____ мс

R, Ом	Q1, мкКл	Q2, мкКл	Q3, мкКл	Q4, мкКл	Q5, мкКл	Q6, мкКл	, мс	, с-1
1
2
3
4
5
6
t, мс

4.3.4. Обработка результатов измерений

1. 
   Рассчитайте по формуле (4.3.5) значение периода колебаний и запишите его над табл. 4.3.2.
   
2. 
   Рассчитайте время t, при котором измерена соответствующая амплитуда, и запишите в табл. 4.3.2 (t₁ = T, t₂ = 2T, t₃ = 3T и т. д.).
   
3. 
   Запишите из окна модели значение времени затухания .
   
4. 
   Рассчитайте величины коэффициента затухания  = 1/ и также внесите в табл. 4.3.2.
   
5. 
   Постройте график зависимости коэффициента затухания от сопротивления R резистора.
   
6. 
   По наклону графика (R) (см. с. 7)определите индуктивность контура, используя формулу
   

^R

L  . (4.3.11)

2

7. 
   Сравните рассчитанное значение индуктивности с заданным первоначально. Рассчитайте относительную и абсолютную погрешности (см. с.
   

8).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Что называется колебанием?
   
2. 
   Какие колебания называются свободными?
   
3. 
   Что называется колебательным контуром?
   
4. 
   Что такое идеальный колебательный контур?
   
5. 
   Какие колебания называются гармоническими?
   
6. 
   Какие физические величины испытывают колебания в идеальном колебательном контуре?
   
7. 
   Запишите дифференциальное уравнение для заряда конденсатора в контуре в случае свободных незатухающих гармонических колебаний.
   
8. 
   Запишите формулу зависимости заряда на конденсаторе от времени при свободных незатухающих колебаниях в контуре.
   
9. 
   Запишите дифференциальное уравнение для заряда конденсатора в контуре в случае свободных затухающих колебаний.
   
10. 
    Запишите формулу зависимости заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре.
    
11. 
    Запишите формулу Томсона для периода колебаний.
    
12. 
    Напишите формулу для коэффициента затухания и частоты затухающих колебаний.
    
13. 
    Что называется временем затухания?
    
14. 
    Чему равен логарифмический декремент затухания?
    
15. 
    Как определяется добротность колебательного контура?
    
16. 
    Как определяется графически время затухания?