шпора2. Электрическая цепь и её элементы
 Скачать 1.35 Mb.
|
|
Параллелное соединение индуктивно связанных элементов цепи Две катушки с сопротивлениями R1 и R2, индуктивностями L1 и L2 и взаимной индуктивностью М соединены параллельно, причем одноимённые выводы присоединены к одному и тому же узлу (рис. 4.7). При выбранных положительных направлениях токов и напряжения получаем следующие выражения:    где 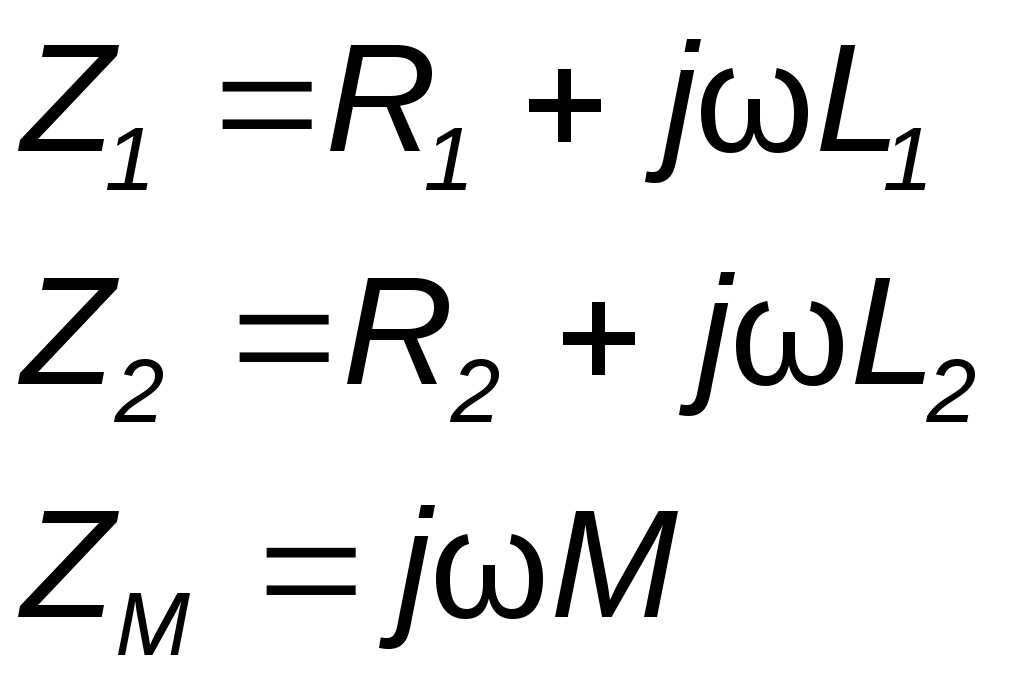 В этих уравнениях комплексные напряжения 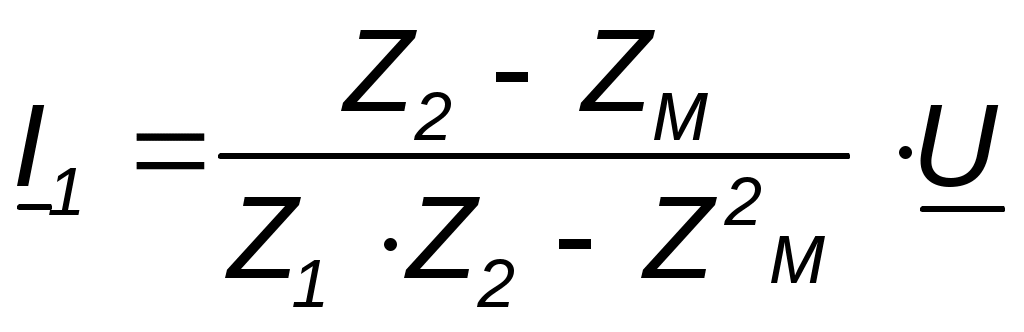 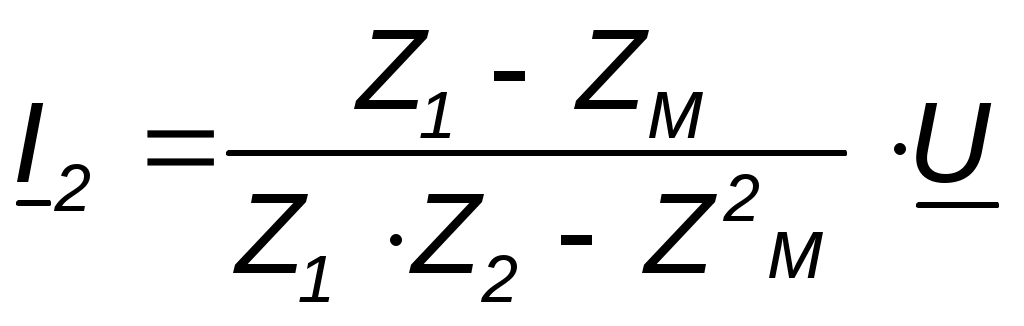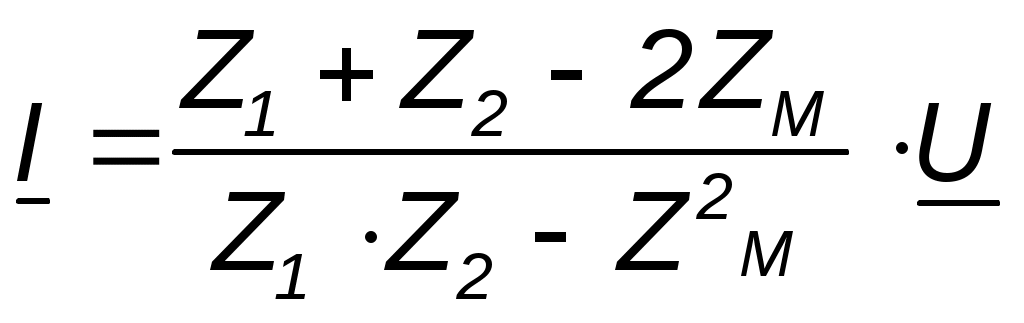и  взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных выводов одинаково. Решив уравнения, получим   Откуда следует, что входное комплексное сопротивление рассматриваемой цепи 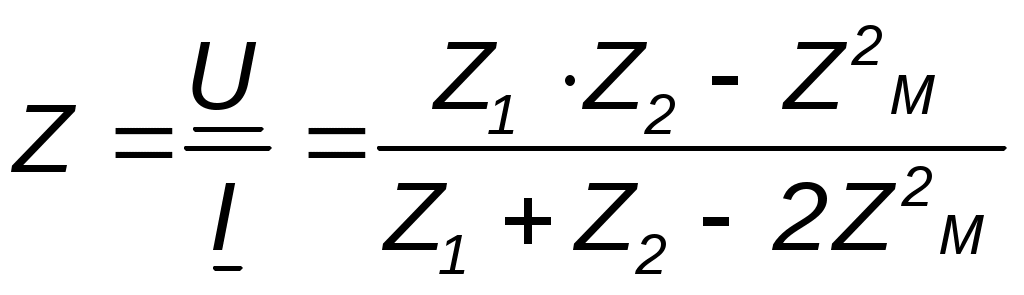 РАСЧЁТ ТРЁХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Основные понятия и определения Объединение в одной линии электропередачи нескольких цепей переменного тока с независимыми источниками электроэнергии называется многофазной системой. Трёхфазной симметричной системой Э.Д.С. называется совокупность трёх Э.Д.С. одинаковой частоты и амплитуды, сдвинутых друг относительно друга по фазе на 1200 . Эти три Э.Д.С. можно изобразить на временной (рис.5.1) и векторной (рис. 5.2.) диаграммах. Т 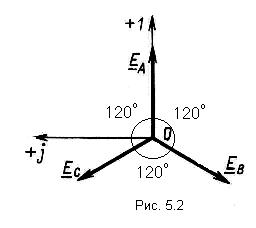 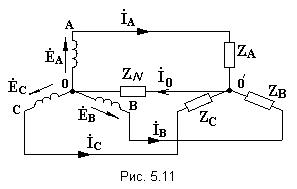   рёхфазные симметричные системы Э.Д.С. получаются с помощью трёхфазного генератора, в котором имеются три самостоятельные обмотки, расположенные на статоре, и сдвинутые относительно друг друга в пространстве на 1200. В центре статора вращается магнит (рис. 5.3). Форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по синусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироваться Э.Д.С. равной амплитуды и частоты, отличающиеся друг от друга на 1200 .   Комплексы действующих значений этих Э.Д.С.: 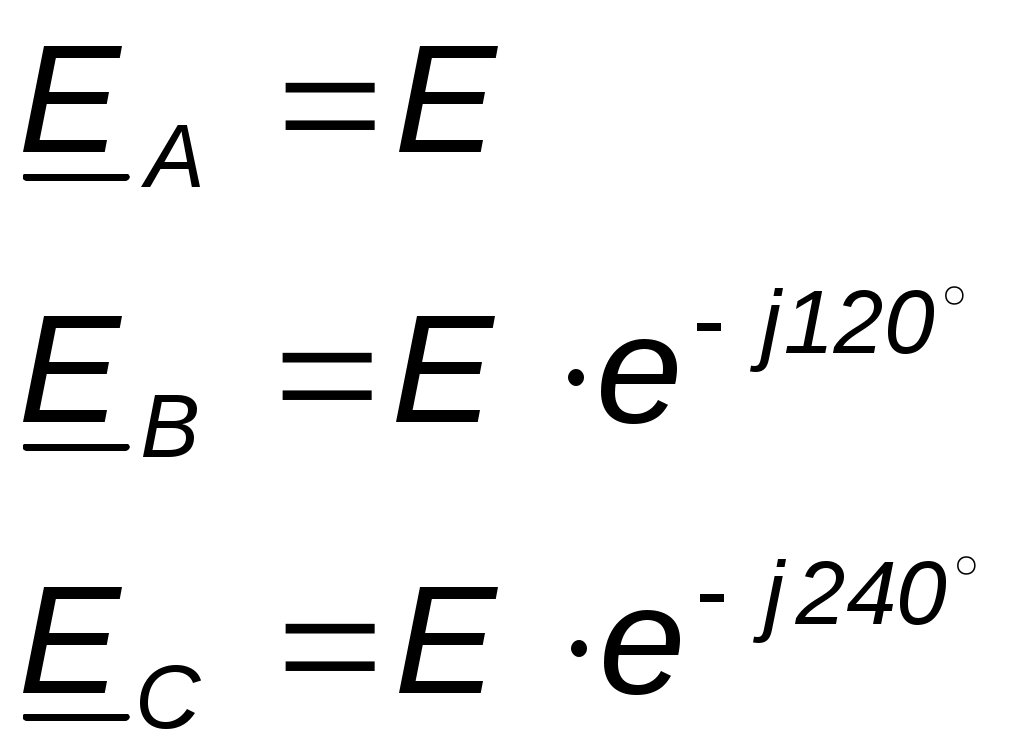 Основные схемы соединения трёхфазных цепей 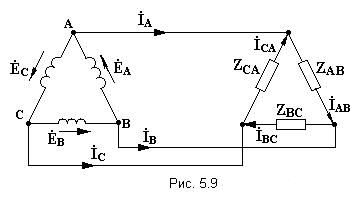 Существуют различные способы соединения обмоток генератора с нагрузкой, но в целях экономии обмотки трёхфазного генератора соединяют в звезду или в треугольник. При соединении в звезду концы обмоток генератора объединяются в одну точку О, которая называется нулевой, или нейтральной. 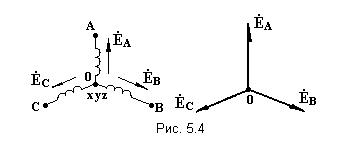 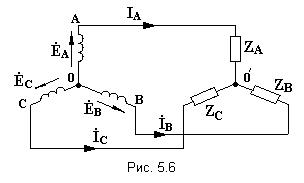 Ниже приведены схемы соединения трёхфазного генератора с трёхфазной нагрузкой по схеме звезда без нулевого провода 1) Точку, в которой объединяют три конца трёхфазной нагрузки при соединении её звездой, называют нулевой точкой нагрузки и обозначают О’. 2) Провода, соединяющие точки А, В, С генератора с точками а,b,с нагрузки, называют линейными. 3) Нулевым проводом называют провод, соединяющий нулевые точки генератора и нагрузки 4) Линейными токами Iл называют токи текущего линейным проводам (их обозначают  , ,  )5) Фазным напряжением Uф называют напряжение между началом и концом фазы или между линейным и нулевым проводом (их обозначают  ).6) Линейным напряжением UЛ называют напряжение между двумя линейными проводами ( их обозначают  ).7) Фазные и линейные напряжения связаны между собой выражениями 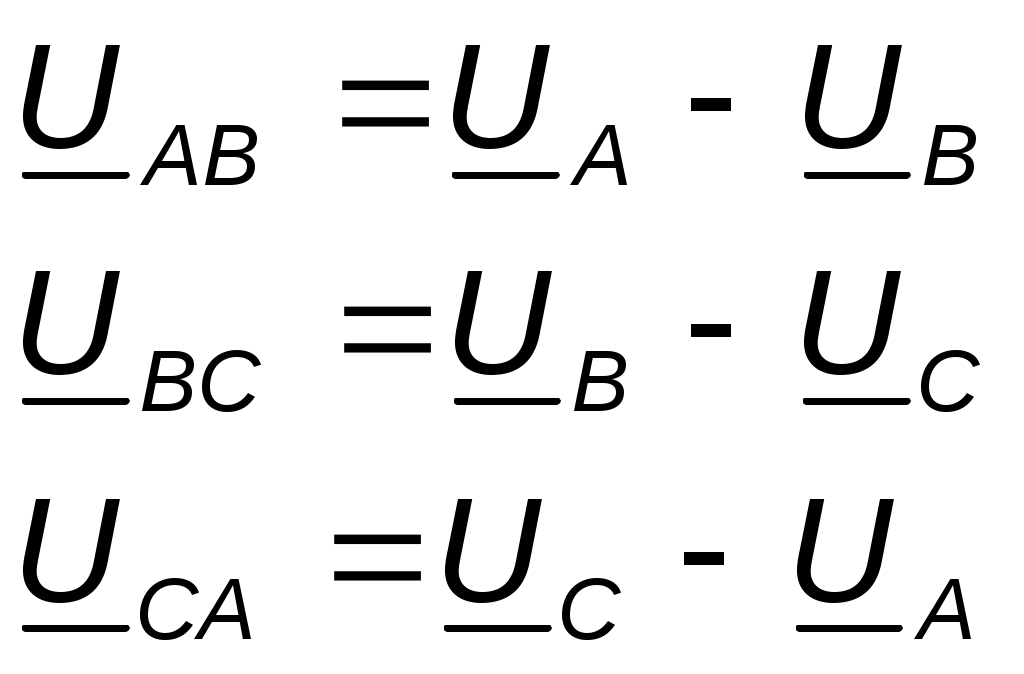 В 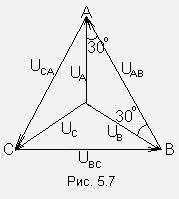 симметричной системе фазных напряжений система линейных напряжений тоже симметрична:  равны по величине и сдвинуты относительно друг друга на 1200  Таким образом, получим общее соотношение между линейными и фазными напряжениями в симметричной системе 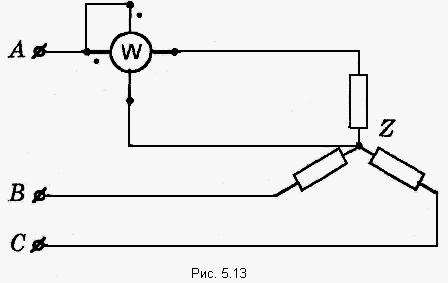  Методы расчета трёхфазных цепей Соединение звездой Нагрузка в трёхфазной цепи может быть: 1) симметричной, если сопротивления фаз нагрузки одинаковы по характеру и значению; 2) несимметричной, если сопротивления фаз нагрузки различны. Рассмотрим наиболее общий случай расчёта цепи с нулевым проводом, сопротивление которого ZN Если нужно учесть сопротивления линейных проводов и фаз источника их можно отнести к нагрузке, прибавив к сопротивлениям последнего по правилам сложения комплексных чисел. Наиболее удобным методом расчёта в данном случае является метод узлового напряжения: 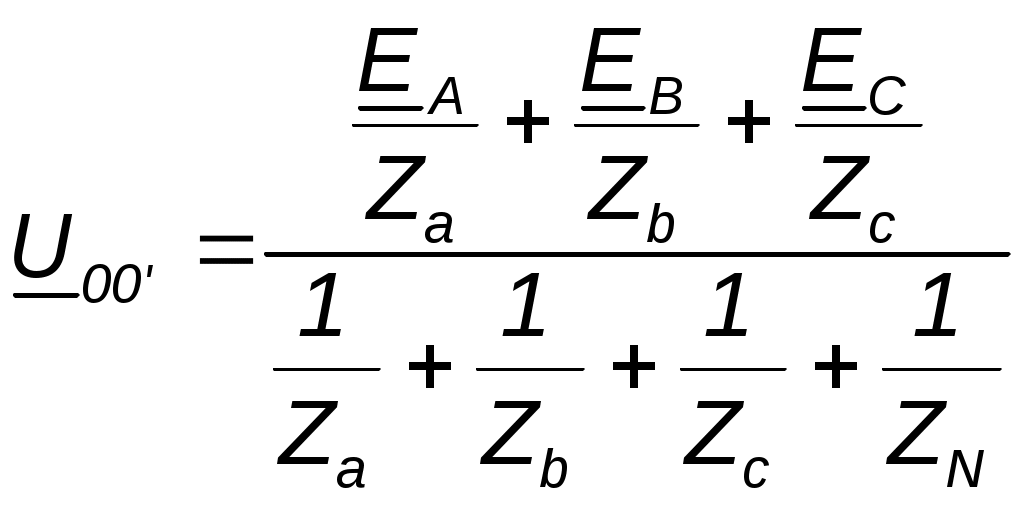 Напряжения на фазах нагрузки: 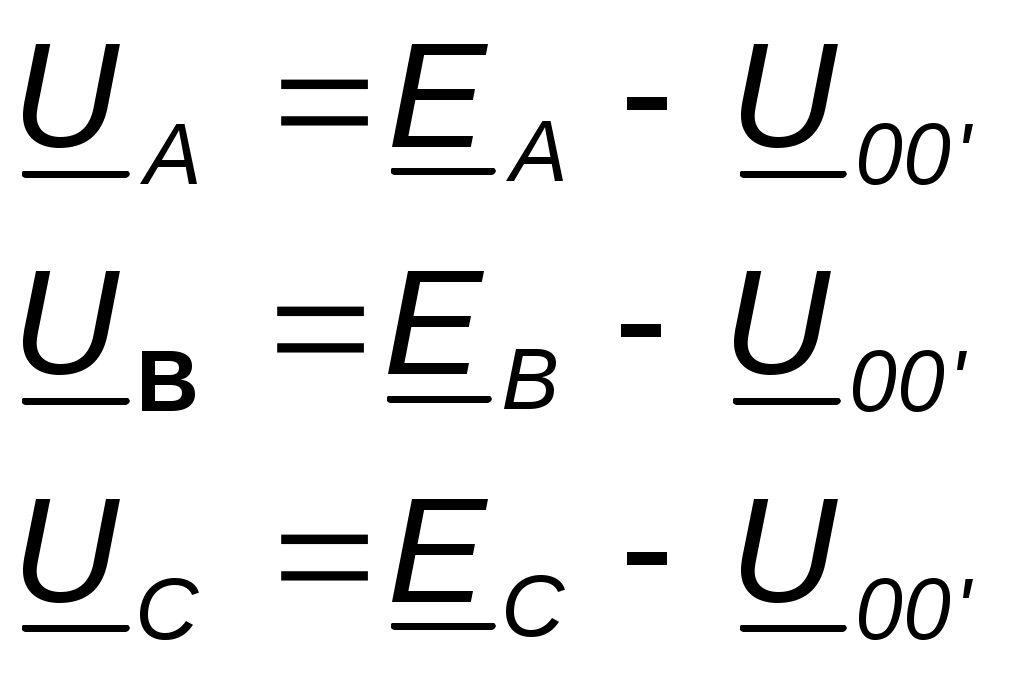 Методы расчета трёхфазных цепей Соединение треугольником Трёхфазная цепь при соединении источника и приёмника треугольником имеет разветвлённую многоконтурную схему. Расчёт этой сложной цепи значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приёмника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему. Если трёхфазная система напряжений, приложенных к приёмнику, известна, то фазные токи в симметричном приёмнике определяются порознь по известным формулам:  Токи в линейных проводах: 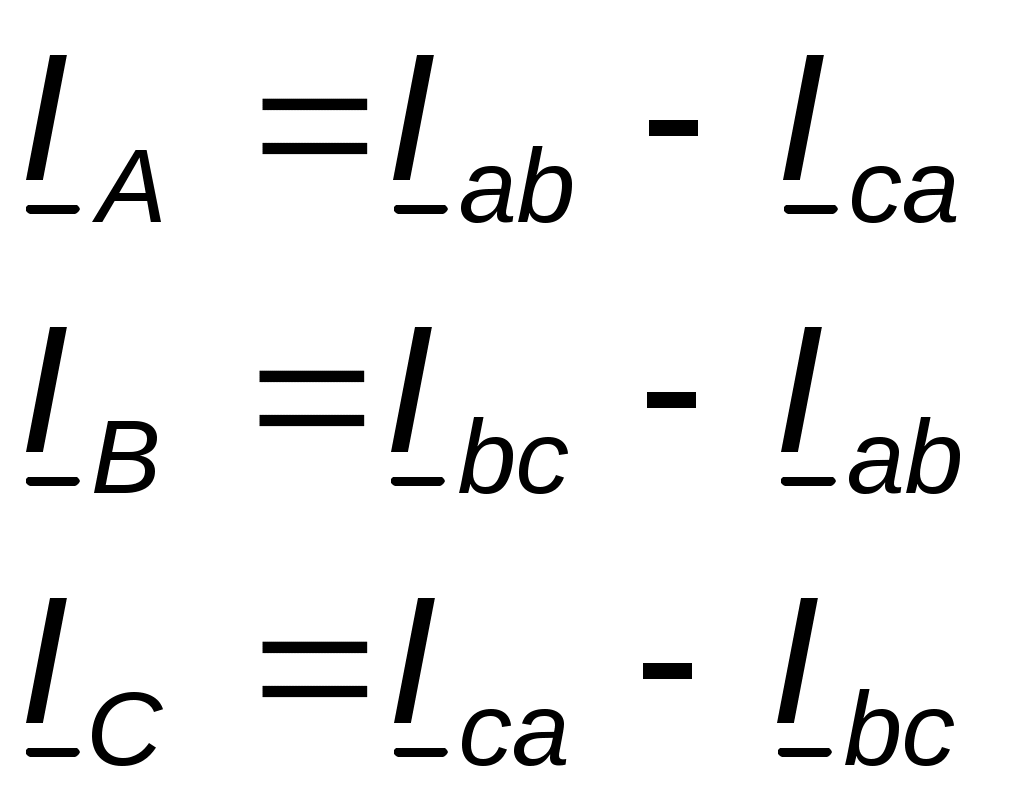 Если же сопротивления линейных проводов необходимо учитывать, то для расчёта цепи следует преобразовать треугольник сопротивления нагрузки в звезду, определить токи в линейных проводах с учётом формулы и затем найти напряжения и токи фаз нагрузки. При симметричной нагрузке фаз достаточно провести расчёт одной фазы. Измерение мощности в трёхфазных цепях Активной мощностью трехфазной системы называют сумму активных мощностей ее отдельных фаз:  При симметричной нагрузке мощности отдельных фаз равны между собой, а общая мощность определяется как  На практике мощность трехфазной системы чаще выражают через линейные, а не через фазные токи и напряжения. 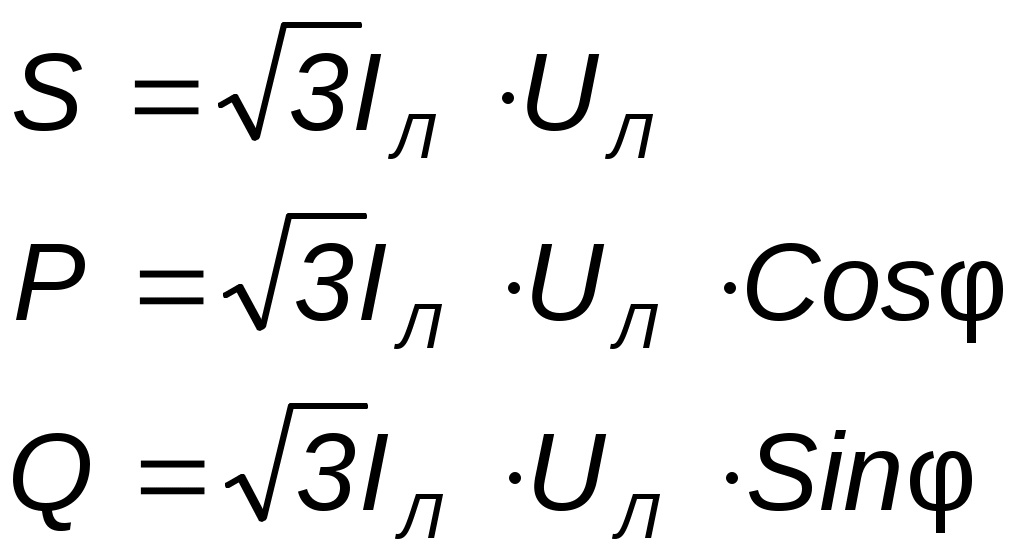 Для трехфазной системы также справедливы следующие соотношения для полной, активной и реактивной мощностей, соответственно: Существуют несколько методов измерения мощности трехфазной системы, у каждого из них своя область применения. Способ одного ваттметра. Используют для измерения мощности при симметричной нагрузке, соединенной звездой с доступной нулевой точкой В этом случае общая мощность трехфазной системы равна утроенному показанию ваттметра:  2) Определить показания вольтметра pVи указать, в каких режимах работают источники ЭДС (Ri, Ом, Ej, B) По второму закону Кирхгофа: E1- E2 = R1I+ R2I= (R1+ R2)I, I=(E1- E2) /(R1+ R2) == (60-10) / (30+20) Показание вольтметра не зависит от того, какая часть схемы рассматривается с целью его определения. Для определения показания вольтметра составляется уравнение, согласно II закону Кирхгофа Е1 = R1 I + Uab, Uab = E1 – R1 I или Е2 = R2 I + Uab , Uab = E2 – R2 I |