шпора2. Электрическая цепь и её элементы
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
Принцип наложения и метод наложения Е 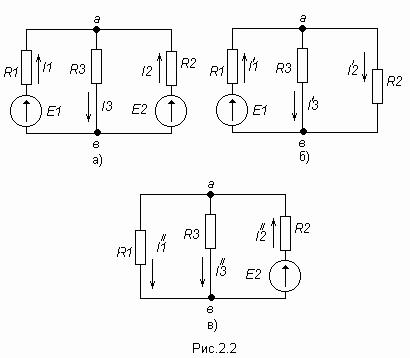 щё один метод расчета линейных электрических цепей называется методом наложения. В его основе лежит принцип наложения, который можно сформулировать следующим образом: ток в любой ветви равен алгебраической сумме токов, вызываемых каждой из Э.Д.С. схемы в отдельности. Н 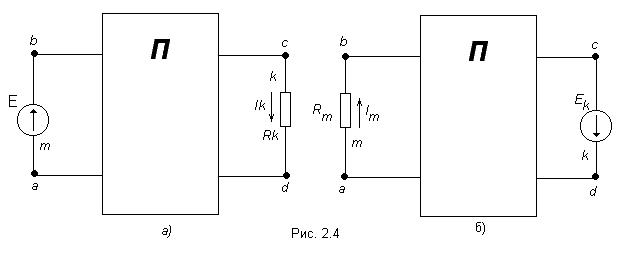 а исходной схеме (рис 2.2а) произвольно выбираем направления токов. Рассчитываем цепь от действия Э.Д.С. Е1, для чего мысленно закорачиваем (убираем) все остальные Э.Д.С., в нашем случае Э.Д.С. Е2 (рис 2.2б). 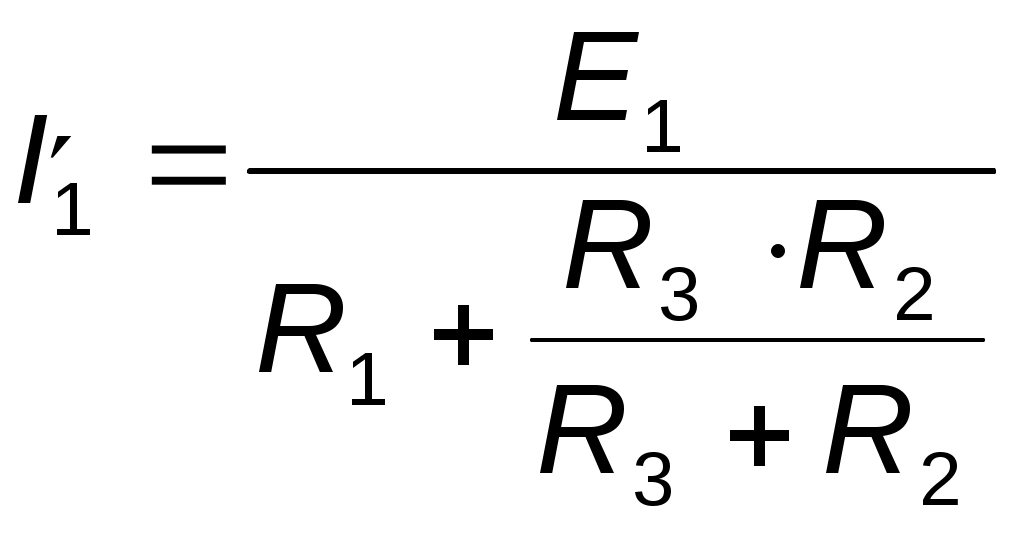 Рассчитываем цепь от действия Э.Д.С. Е2, для чего мысленно закорачиваем Э.Д.С. Е1 (рис 2.2в) Действительные токи находим как алгебраическую сумму найденных частичных токов. Значения токов В 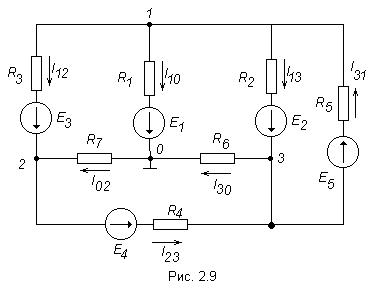 ходные и взаимные проводимости ветвей ходные и взаимные проводимости ветвейН 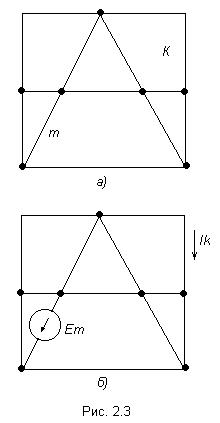 а рис. 2.3а изображена скелетная схема пассивной цепи. В каждой её ветви есть сопротивление. Выделим две схемы ветви m и k. Поместим в ветвь m Э.Д.С. (рис 2.3б). Выберем контуры в схеме так, чтобы k- ветвь входила только в k- контур, а m- ветвь, только в m-контур. Э.Д.С. Em вызовет точки в ветвях m и k. а рис. 2.3а изображена скелетная схема пассивной цепи. В каждой её ветви есть сопротивление. Выделим две схемы ветви m и k. Поместим в ветвь m Э.Д.С. (рис 2.3б). Выберем контуры в схеме так, чтобы k- ветвь входила только в k- контур, а m- ветвь, только в m-контур. Э.Д.С. Em вызовет точки в ветвях m и k.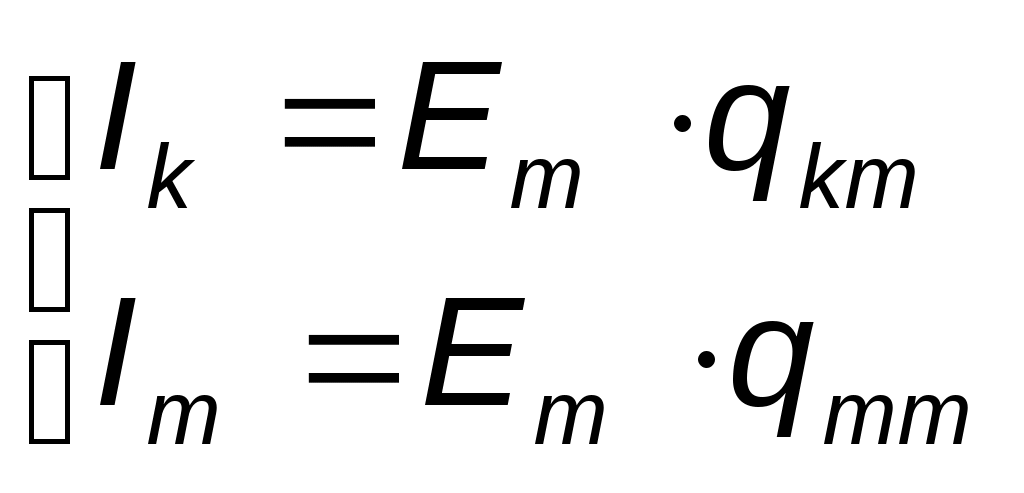 Коэффициенты q имеют размерность проводимости. Коэффициент qmm называют входной проводимостью ветви m, qkm – взаимной проводимостью. Для расчёта проводимостей составляют уравнения по методу контурных токов, следя за тем, чтобы ветви, взаимные и входные проводимости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы ∆ и по нему необходимые алгебраические дополнения. Теорема взаимности Теорема взаимности формируется таким образом: для любой линейной цепи с одним источником Э.Д.С. ток Ik в ветвях, вызванный Э.Д.С. Em, находящийся в m-ветви, будет равен току Im в m-ветви, вызванному Э.Д.С. Ek (численно равной Em) находящейся в k ветви. Другими словами, сущность принципа взаимности состоит в следующем. Пусть имеется электрическая схема произвольной конфигурации с единственным источником Э.Д.С. Em, который действует в m-ветви в направлении от точки а к точке в (рис 2.4а) и создаёт в k-ветви с сопротивлением Rk ток Ik, направленный от точки с к точке d. Такой же источник Э.Д.С. Ek = Em, включенный в k-ветвь и действующий от точки c к точке d (рис 2.4б) создаёт в m-ветви с сопротивлением Rm = Rk ток Im, направленный от точки а к точке b и равный току Ik. На рис. 2.4 пассивным четырёхполюсником (прямоугольником с буквой П) обозначена вся остальная часть схемы, не содержащая источников Э.Д.С. и источников тока. Токи в ветвях m и k. Можно отметить, что теорема взаимности справедлива не только для токов, но и для напряжений. Метод узловых потенциалов В  тех случаях, когда в анализируемой схеме число узлов без единицы меньше числа независимых контуров, метод узловых потенциалов является более экономичным по сравнению с методом контурных токов. Суть этого метода состоит в определении напряжений между узлами сложной электрической цепи путём решения системы уравнений, составленных на основе первого закона Кирхгофа. После нахождения неизвестных потенциалов, используя закон Ома, определяют токи во всех ветвях, и выясняют их истинное направление. Потенциал любой одной точки схемы можно принять равным нулю, так как ток в ветви зависит не от абсолютных значений потенциалов узлов, а от разности потенциалов на концах ветви. При этом число неизвестных уменьшается с n до n -1. Рассмотрим применение данного метода для расчета цепи, приведённой на рис. 2.9, которая имеет большое число ветвей (7) и сравнительно небольшое число узлов (4). Если узел 0 мысленно заземлить, то есть принять его потенциал равным 0, то неизвестными будут потенциалы только трёх узлов: П 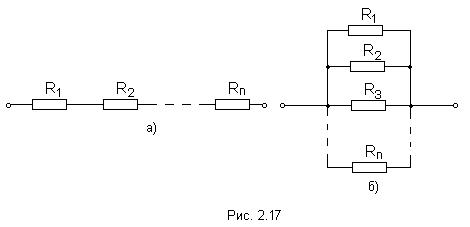 ервоначально в исходной схеме произвольно задаём направления токов, которые обозначаются с двумя индексами: первый индекс определяет номер узла, от которого течет ток, а второй - номер узла, к которому ток подтекает. 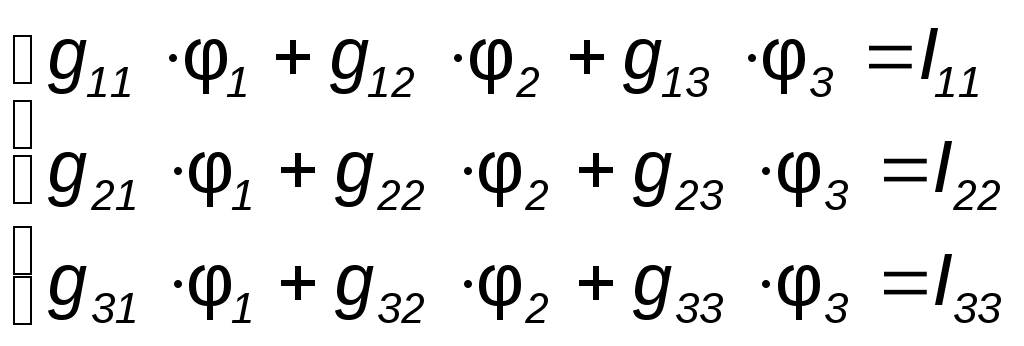 1 и 2, принято всегда брать со знаком «-». Метод эквивалентного генератора П 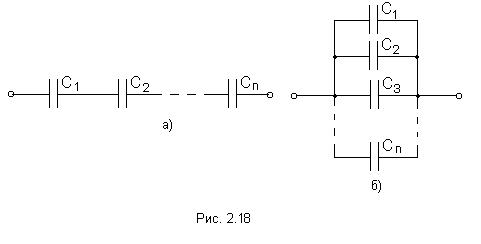 ри расчёте сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объём этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно производить несколько раз, задаваясь различными значениями сопротивления. ри расчёте сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объём этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно производить несколько раз, задаваясь различными значениями сопротивления.В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от структуры и сложности, условно изобразить прямоугольником, который представляет собой так называемый двухполюсник. Таким образом, двухполюсник - это обобщённое название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник Э.Д.С. или тока, то такой двухполюсник называют активным. Если в двухполюснике нет источника Э.Д.С. или тока, то его называют пассивным. При решении задачи методом эквивалентного генератора (активного двухполюсника) необходимо: 1 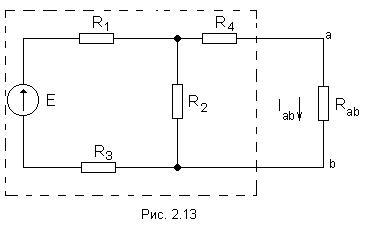 ) Мысленно заключить всю схему, содержащую Э.Д.С. и сопротивления, в прямоугольник, выделив из нее ветвь аb, в которой требуется найти ток (рис 2.13). 2 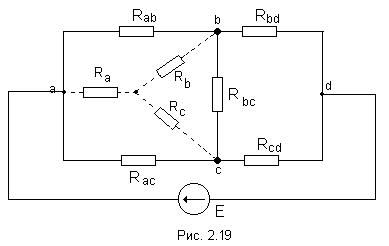 ) Найти напряжение на зажимах разомкнутой ветви ab (в режиме холостого хода). Напряжение холостого хода Uо (эквивалентное Э.Д.С. Еэ) для рассматриваемой цепи можно найти так: Сопротивление R4 в расчёт не вошло, так как при разомкнутой ветви ab ток по нему не протекает. 3)айти эквивалентное сопротивление. При этом источники Э.Д.С. закорачиваются, а ветви, содержащие источники тока, размыкаются. Двухполюсник становится пассивным. Д 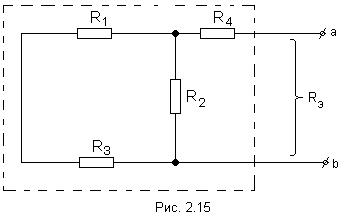 ля данной схемы 4) числить значение тока. Для данной схемы имеем: Преобразования в линейных электрических цепях Соединение резисторов. Существует два вида соединения резисторов: последовательное и параллельное (рис. 2.17). При последовательном соединении резисторов (рис. 2.17а) через все резисторы протекает один и тот же ток I, то есть: Напряжение же U равно сумме падений напряжений на сопротивлениях: Общее сопротивление R рассчитывается При параллельном соединении резисторов(.17б) Общее сопротивление R участка цепи рассчитывается по формуле: Соединение конденсаторов. На рис. 2.18 изображены два способа соединения конденсаторов - последовательное и параллельное. При последовательном соединении конденсаторов (рис. 2.18а) В отличие от резисторов общая ёмкость конденсаторов рассчитывается по формуле: При параллельном соединении конденсаторов (рис. 2.18б). Общая ёмкость рассчитывается следующим образом Замена треугольника сопротивлений эквивалентной звездой и наоборот. Несмотря на то, что эта схема имеет один источник питания, она не поддаётся расчету методом эквивалентных сопротивлений, так как в ней нет сопротивлений, включенных между собой последовательно или параллельно. Особенностью этой схемы является наличие замкнутых контуров из трёх сопротивлений (Rab, Rbc, Rac и Rbd, Rcd, Rbc) причём точки, разделяющие каждую пару смежных сопротивлений, являются узловыми. Такие контуры называются треугольниками сопротивлений. Воспользуемся способом расчета, который состоит в замене треугольника сопротивлений эквивалентной трёхлучевой звездой сопротивлений (Ra, Rb, Rc ) как показано на рис. 2.19 пунктиром. Замена треугольника сопротивлений эквивалентной звездой, и наоборот, осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды. Одновременно предполагается, что в остальной части схемы, незатронутой преобразованием, режим работы не изменяется (не изменяются токи, напряжения, мощности). Без доказательства приведём формулы, которые служат для определения сопротивлений трёхлучевой звезды по известным сопротивлениям эквивалентного треугольника. Обратное преобразование трёхлучевой звезды в эквивалентный треугольник, осуществляется Синусоидальный ток и его основные характеристики В настоящее время переменный ток находит широкое применение в технике, так как он легко трансформируется и передается на большие расстояния при высоком напряжении и малых потерях. В электротехнике наибольшее распространение получил синусоидальный переменный ток, то есть ток, величина которого изменяется по закону синуса. Поэтому мгновенное значение синусоидального тока выражается формулой где Т - период – время, за которое совершается одно полное колебание, с; 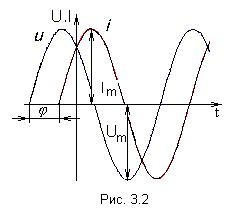 f = 1/T - частота, равная числу колебаний за 1 секунду (единица измерения частоты – Герц (Гц) или с-1 ); ω – угловая частота (выражается в рад/с или с-1 ). Аргумент синуса, то есть Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой. Если частота слишком низкая, то увеличиваются габариты электрических машин и, следовательно, расход материалов на их изготовление. При слишком больших частотах увеличиваются потери энергии в сердечниках электрических машин и трансформаторах. Среднее и действующее значения синусоидально изменяющейся величины Под средним значением синусоидально изменяющейся величины понимают её среднее значение за полпериода. 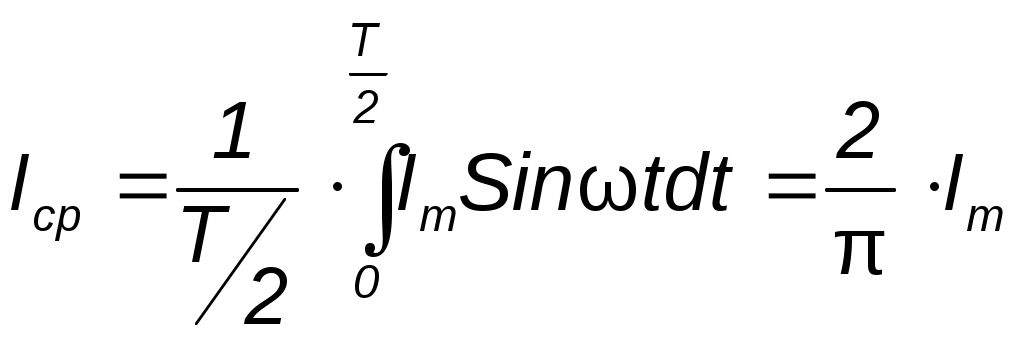 То есть среднее значение синусоидального тока составляет Переменный ток обычно характеризуется его действующим значением 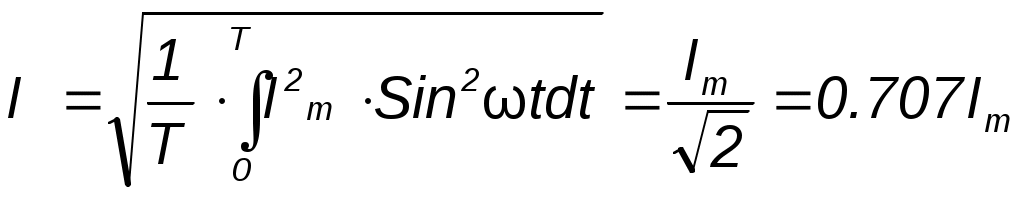 Значит, действующее значение синусоидального тока равно 0,707 от амплитудного. Значит, действующее значение синусоидального тока равно 0,707 от амплитудного. |
